Made by Morenshildt I.K. group 1.45.36 Frunzensky district School No. 314 Teacher Koroleva O.P. St. Petersburg 2006 * St. Petersburg CENTER FOR INFORMATION TECHNOLOGIES AND TELECOMMUNICATIONS MUTUAL INVERSE FUNCTIONS
Exponential and logarithmic function Trigonometric functions
Basic Definitions Example Equations Graphs of Inverse Functions Exponential and Logarithmic Functions Sine and Arcsine Functions Cosine and Arccosine Functions Tangent and Arctangent Functions Cotangent and Arccotangent Functions Exam Sources Contents Finish
Reversible function If the function y=f (x) takes each of its values only for one value of x, then this function is called reversible. For such a function, it is possible to express the inverse relationship between the values of the argument and the values of the function.
An example of constructing a function inverse to a given one Particular case Given a function y=3x+5 Equation for x Replace x by y Functions (1) and (2) are mutually inverse General case y=f (x) is an invertible function Defined function x= g (y ) Replace x with y y= g(x) The functions y=f(x) and y=g(x) are mutually inverse
Graphs of inverse functions
Exponential and logarithmic functions y=log a x y=a x y=x a>1
Functions sin x and arcsin x Consider the function y=sin x on the segment The function is monotonically increasing. FZF [-1;1]. The function y= arcsin x is the inverse of the function y=sinx . [ - ; ] 2 2
Functions cos x and arccos x Consider the function y=co s x on the segment The function is monotonically decreasing. FZF [-1;1]. The function y=arccos x is the inverse of the function y=co sx .
Functions tg x and arctg x Consider the function y= tg x on the interval The function is monotonically increasing. ORF is the set R . The function y= arctg x is the inverse of the function y= tg x . (- ; ) 2 2
Functions ctg x and arcctg x Consider the function y= ctg x on the interval (0; ). The function is monotonically decreasing. The GFA is the set R . The inverse is the function y \u003d arcctg x.
Test on the topic "Mutually inverse functions" Question No. 1 Question No. 2 Question No. 3 Question No. 4 Question No. 5 Finish Finish
Question No. 1 Graphs of mutually inverse functions are located in the coordinate system symmetrically with respect to: The origin of coordinates Direct y \u003d x Axes OY Axes OX
Question No. 2 How are the domain of definition of the original and the domain of the inverse function related? Match Independent
Question #3 What is the inverse of a logarithmic function? Power Linear Quadratic Exponential
Question #4 The function y=arcctg x is the inverse of the function y=sin x y= tg x y= ctg x y= cos x
Question #5 The topic “Reciprocal Functions” is Elementary My Favorite Easy Understandable
Hooray! Hooray! Hooray! Well done scientist!
Wrong answer Repeat from the beginning!
Wrong! I'm outraged by your answer!
Sources of Algebra and the Beginnings of Analysis: Proc. for 10-11 cells. general education institutions / Sh.A. Alimov, Yu.M. Kolyagin, Yu.V. Sidorov and others - 12th ed. - M.: Enlightenment, 2004. - 384 p. The study of algebra and the beginning of analysis in grades 10-11: Book. for the teacher / N.E. Fedorova, M.V. Tkachev. - 2nd ed. - M .: Education, 2004. - 205 p. Didactic materials on algebra and the beginnings of analysis for grade 10: A guide for the teacher / B.M. Ivlev, S.M. Sahakyan, S.I. Schwarzburd. - 2nd ed., revised. - M.: Enlightenment, 1998. -143 p. Graphs of inverse trigonometric functions http://chernovskoe.narod.ru/tema13.htm
Topic: "Mutually inverse functions".
Lesson Objectives:
Educational:
Repeat and summarize the knowledge of students on the topic "Function", studied in grade 9. To get acquainted with mutually inverse functions, to study the conditions for the existence of an inverse function and its properties, to learn how to build graphs of inverse functions.
Developing:
To develop the creative and mental activity of students, their intellectual qualities: the ability to "see" the problem.
To form the ability to clearly and clearly express their thoughts, explore, analyze, compare, draw conclusions.
To develop students' interest in independent creativity.
Develop students' spatial imagination.
Educational:
To develop the ability to work with available information in an unusual situation.
Cultivate accuracy and conscientiousness.
Carry out aesthetic education.
Lesson type: combined.
Equipment:
multimedia projector;
application to the lesson: (Presentation.) - on electronic media;
Means of education: computers, softwareexcel, media projector, slide presentation.
Demos: graphs of functions built in one coordinate system.
Forms of organization of educational activities: individual, dialogue, work with the text of the slide, research work in a notebook.
Methods: visual, verbal graphic, research.
During the classes.
1. Introductory speech of the teacher. Installation conversation. Psychological mood of students.
In the lesson, we must repeat and summarize the knowledge on the topic "Function" studied in grade 9, get acquainted with mutually inverse functions, study the conditions for the existence of an inverse function and its properties, learn how to build graphs of inverse functions. We wish each other success and fruitful work.
2. Repetition of the material covered on the topic "Functions and their graphs." Presentation.
Slides 2-10. Frontal work with the class.





3. Learning new material. Educational conversation with elements of research and demonstration (slides 11-24)



Dependency example. Each function value corresponds to one argument value.
For such functions, it is possible to express the inverse relationship between the values of the argument and the values of the function.


Exercise.

Find the domain and range of mutually inverse functions.




4. Consolidation of knowledge.




Lesson notes on the topic "Inverse functions"
Lesson 1 "Reverse Function"
Target: Form a theoretical apparatus on the topic. Enter
The concept of an invertible function;
The concept of an inverse function;
Formulate and prove a sufficient condition for reversibility
functions;
Basic properties of mutually inverse functions.
Lecture lesson plan
Organizing time.
Actualization of students' knowledge, necessary for the perception of a new topic.
Presentation of new material.
Summing up the lesson.
The course of the lesson-lecture
1. Organizing time.
2. Knowledge update. ( Frontal survey on the topic of the previous lesson.)
For students, a graph of the function is shown on the interactive board (Fig. 1). The teacher formulates the task - to consider the graph of the function and list the studied properties of the function. Students list the properties of a function according to the research design. The teacher, to the right of the graph of the function, writes down the named properties with a marker on the interactive whiteboard.
Rice. 1
Function properties:
3. Goal setting for students.
At the end of the study, the teacher reports that today at the lesson they will get acquainted with one more property of the function - reversibility. For a meaningful study of new material, the teacher invites the children to get acquainted with the main questions that students must answer at the end of the lesson. Each student has questions in the form of a handout (distributed before the lesson).
Questions:
1. What function is called reversible?
2. What function is called inverse?
3. How are the domains of definition and the sets of values of direct and inverse functions related?
4. Formulate a sufficient condition for the function to be invertible.
5. Is the inverse of an increasing function decreasing or increasing?
6. Is the inverse odd function even or odd?
7. How are the graphs of mutually inverse functions arranged?
4. Presentation of new material.
1) The concept of an invertible function. A sufficient condition for reversibility.
On the interactive board, the teacher compares the graphs of two functions whose domains of definition and sets of values are the same, but one of the functions is monotonic and the other is not (Fig. 2). Thus, a function has a property that is not characteristic of a function: no matter what number from the set of function valuesf ( x ) take it, it is the value of the function at only one point, thus the teacher brings students to the concept of an invertible function.
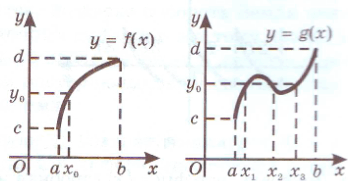
Rice. 2
The teacher then formulates the definition of an invertible function and proves the invertible function theorem using the monotonic function graph on the interactive whiteboard.
Definition 1. The function is calledreversible , if it takes any of its values only at one point of the setX .
Theorem. If the function is monotonic on the setX , then it is reversible.
Proof:
Let the function y=f(x) increases on the setX let it go X 1 ≠x 2 - two points of the setX .
For definiteness, letX 1 < X 2 . Then from whatX 1 < X 2 as the function increases, it follows thatf(x 1 ) < f(x 2 ) .
Thus, different values of the argument correspond to different values of the function, i.e. the function is reversible.
The theorem is proved similarly in the case of a decreasing function.
(During the proof of the theorem, the teacher makes all the necessary explanations on the drawing with a marker)
Before formulating the definition of an inverse function, the teacher asks students to determine which of the proposed functions is reversible? The interactive board shows graphs of functions (Fig. 3, 4) and several analytically specified functions are recorded:
A
)
b
)
Rice. 3 Fig. 4
V ) y=2x+5; G ) y = - + 7.
Comment. The monotonicity of a function, issufficient condition for the existence of an inverse function. But itis not necessary condition.
The teacher gives examples of different situations when the function is not monotonic but reversible, when the function is not monotonic and not reversible, when it is monotonic and reversible.
2) The concept of an inverse function. Algorithm for compiling an inverse function.
Definition 2. Let the reversible functiony=f(x) defined on the setX and its rangeE(f)=Y . Let's match eachy from Y then the only meaningX, at which f(x)=y. Then we get a function that is defined onY, A X – range of function values. This function is denotedx=f -1 (y), and call reverse with respect to functiony=f(x), .
Then the teacher introduces students to the method of finding the inverse function given analytically.
Algorithm for compiling an inverse function for a function y = f ( x ), .
Make sure the functiony=f(x) reversible on the intervalX .
Express variableX through at from the equation y=f(x), taking into account that.
In the resulting equality, swapX And at. Instead of x=f -1 (y) write y=f -1 (x).
With specific examples, the teacher shows how to use this algorithm.
Example 1 Show what's for a functiony=2x-5
Solution . Linear functiony=2x-5 determined on R, increases by R and its range isR. So the inverse function exists onR . To find its analytical expression, we solve the equationy=2x-5 relatively X ; get. Rename the variables, we get the desired inverse function. It is defined and increases by R.
Example 2 Show what's for a functiony=x 2 , x ≤ 0 exists an inverse function, and find its analytic expression.
Solution . The function is continuous, monotone in its domain of definition, therefore, it is invertible. After analyzing the domains of definition and the set of values of the function, the corresponding conclusion is made about the analytical expression for the inverse function, which has the form.
3) Properties of mutually inverse functions.
Property 1. If g is the function inverse to f , then and f is the function inverse to g (the functions are mutually inverse), whileD ( g )= E ( f ), E ( g )= D ( f ) .
Property 2. If a function is increasing (decreasing) on the set X, and Y is the range of the function, then the inverse function is increasing (decreasing) on Y.
Property 3. To get a graph of a function that is inverse to a function, it is necessary to transform the graph of the function symmetrically with respect to the straight liney=x .
Property 4. If an odd function is invertible, then its inverse is also odd.
Property 5. If functions f ( x ) And mutually inverse, then it is true for any, and true for any.
Example 3 Plot the inverse function if possible.
Solution. This function has no inverse over its entire domain of definition, since it is not monotonic. Therefore, consider the interval on which the function is monotonic: , hence, there is an inverse. Let's findher . For this, we expressx throughy : . Rename - inverse function. Let's build graphs of functions (Fig. 5) and make sure that they are symmetrical with respect to a straight liney = x .

Rice. 5
Example 4 Find the set of values of each of the mutually inverse functions, if you know that.
Solution. According to property 1 of mutually inverse functions, we have.
5 . Summarizing
Carrying out diagnostic work. The purpose of this work is to determine the level of assimilation of the educational material discussed in the lecture. Students are invited to answer the questions formulated at the beginning of the lecture.
6 . Setting homework.
1. Understand the lecture material, learn the basic definitions and formulations of theorems.
2. Prove the properties of mutually inverse functions.
Lesson 2 A sufficient condition for the invertibility of a function"
Target: to form the ability to apply theoretical knowledge on the topic when solving problems, to consider the main types of problems for studying a function for reversibility, for building an inverse function.
Workshop Lesson Plan:
1. Organizational moment.
2. Actualization of knowledge (frontal work of students).
3. Consolidation of the studied material (problem solving).
4. Summing up the lesson.
5. Statement of homework.
During the classes.
1. Organizing time.
Greeting the teacher, checking the readiness of students for the lesson.
2. Knowledge update. ( front work of students).
Students are asked to complete the following tasks orally:
1. Formulate a sufficient condition for the function to be invertible.
2. Among the functions whose graphs are shown in the figure, indicate those that are reversible.
3. Formulate an algorithm for compiling a function inverse to a given one.
4. Are there functions inverse to data? If yes, find them:
A) ; b ) ; c ) .
5. Are the functions whose graphs are shown in the figure mutually inverse (Fig. 6)? Justify the answer.

Rice. 6
3. Consolidation of the studied material (problem solving).
Consolidation of the studied material consists of two stages:
Individual independent work of students;
Summing up the results of individual work.
At the first stage, students are given cards with tasks that they perform on their own.
Exercise 1.
Is the function reversible over the entire domain of definition? If yes, then find the reverse to it.
a) ; b) ; c).
Task 2.
Are the functions mutually inverse:
A) ;
b ) .
Task 3.
Consider the function on each of the indicated intervals, if the function is invertible on this interval, then set its inverse analytically, indicate the domain of definition and range of values:
a ) R ; b ) ; d ) [-2;0].
Task 4.
Prove that the function is irreversible. Find the function inverse to it on the interval and plot its graph.
Task 5.
Plot the function and determine if there is an inverse function for it. If yes, then plot the inverse function on the same drawing and set it analytically:
a ) ; b ) .
At the stage of summing up the results of the individual work of students, the tasks are checked only with the fixation of intermediate results. The problems that caused the most difficulties are considered on the board either with the disclosure of the search for solutions, or with a record of the entire solution.
4. Summing up the lesson (reflection).
Students are offered a mini-questionnaire:
What did I like about the lesson?______________________________
What did I not like about the lesson? _____________________________
_________________________________________________________________
Choose one statement that best suits you:
1) I can independently investigate the function for reversibility, build the inverse and I am sure that the result is correct.
2) I can examine the function for reversibility, build the inverse, but I'm not always sure of the correctness of the result, I need the help of my comrades.
3) I practically cannot investigate the function for reversibility, build the inverse, I need additional advice from the teacher.
Where can I apply the acquired knowledge?____________________ _________________________________________________________________
5. Setting homework.
№ 10.3, 10.6(c, d), 10.7(c, d), 10.9(c, d), 10.13(c, d), 10.18.(Mordkovich, A.G. Algebra and the beginning of mathematical analysis. Grade 10. At 2 p.m. Part 2. Task book for students of educational institutions (profile level) / A.G. Mordkovich, P.V. Semenov. - M.: Mnemosyne, 2014. - 384 p.)
Mutually inverse functions and their graphs
(generalizing repetition of the material covered)


Which of the graphs corresponds to the graph of the function y=x 3 does it have a reverse?

Which of the graphs corresponds to the graph of the function, does it have an inverse?

Which of the graphs corresponds to the graph
Does it have a reverse function?

Which graph corresponds to the function?
Group 1: answer a) explain why

What function does the graph correspond to? 1 . y \u003d x 3 2. 3 . y \u003d x 4 4. y \u003d x -2 5. 6. y = x -1

on the graph of the function
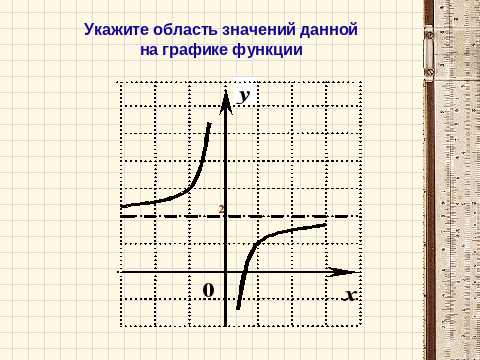
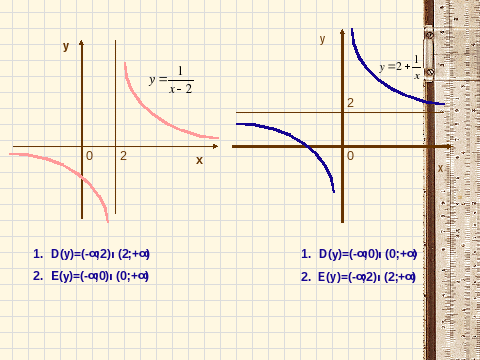
D(y)=(-:0) U(0;+)

Specify the scope of this
on the graph of the function

Specify the range of the given on the graph of the function
E (y)=(- ; 2) U(2 ;+)

Find a function inverse to a given one at = g ( x )
If function (2) is inverse to function (1), then such functions are called mutually inverse.

Find the domain of definition and the set of values for these functions.
- D (y) \u003d (- ∞ ;2) ∪ (2; + ∞)
- E(y)=(- ∞ ;0) ∪ (0;+ ∞)
- D (y) \u003d (- ∞; 0) ∪ (0; + ∞)
2. E(y)= (-∞;2)∪(2;+∞)

- Domain of the inverse function g(x) coincides with the set of values of the original functions f ( x ), and the set of values of the inverse function g(x) coincides with the domain of the original function f(x) :
D( g(x) ) = E( f(x )), E( g(x )) = D( f(x )).
- A monotonic function is reversible:
- if function f (x) increases, then its inverse function g (x) also increases;
- If the function f (x) decreases, then its inverse function g (x) also decreases.

Given: y = x 3
Construct a graph of this function, express the formula of the inverse function of a given function and plot its graph.

3. If the function has an inverse, then the graph of the inverse function is symmetrical to the graph of this function with respect to the straight line y \u003d x.

Construct a graph of a function inverse to a given one.

Teaching independent work
II option
I option
- Find the function inverse to the given one:
2. Find the domain of definition and the set of values of the function inverse to the given one:
3. Construct a graph of the function inverse to the given one:

II option
I option
2. D(y)=(- ; +)
E (y)=(- ; +)
2. D(y)=(- ; +)
E (y)=(- ; +)

Homework:
solve No. 579, No. 576 (c, d
at will No. 581 (1,2)

- During the lesson I learned………………………….
- At the lesson I was interested in …………………....
- It was difficult ………………………………………….
- The knowledge gained in the lesson, I can use …………………………………………
R e f e x i s :
Lesson Objectives:
Educational:
- to form knowledge on a new topic in accordance with the program material;
- to study the property of the invertibility of a function and to teach how to find a function inverse to a given one;
Developing:
- develop self-control skills, subject speech;
- master the concept of an inverse function and learn the methods of finding an inverse function;
Educational: to form communicative competence.
Equipment: computer, projector, screen, SMART Board interactive whiteboard, handout (independent work) for group work.
During the classes.
1. Organizational moment.
Target – preparing students for work in the classroom:
Definition of absent,
Attitude of students to work, organization of attention;
Message about the topic and purpose of the lesson.
2. Updating the basic knowledge of students. front poll.
Target - to establish the correctness and awareness of the studied theoretical material, the repetition of the material covered.<Приложение 1 >
A graph of the function is shown on the interactive whiteboard for students. The teacher formulates the task - to consider the graph of the function and list the studied properties of the function. Students list the properties of a function according to the research design. The teacher, to the right of the graph of the function, writes down the named properties with a marker on the interactive whiteboard.
Function properties:
At the end of the study, the teacher reports that today at the lesson they will get acquainted with one more property of the function - reversibility. For a meaningful study of new material, the teacher invites the children to get acquainted with the main questions that students must answer at the end of the lesson. Questions are written on an ordinary board and each student has a handout (distributed before the lesson)
- What is a reversible function?
- Is every function reversible?
- What is the inverse given function?
- How are the domain of definition and the set of values of a function and its inverse function related?
- If the function is given analytically, how do you define the inverse function with a formula?
- If a function is given graphically, how to plot its inverse function?
3. Explanation of new material.
Target - to form knowledge on a new topic in accordance with the program material; to study the property of the invertibility of a function and to teach how to find a function inverse to a given one; develop subject matter.
The teacher conducts a presentation of the material in accordance with the material of the paragraph. On the interactive board, the teacher compares the graphs of two functions whose domains of definition and sets of values are the same, but one of the functions is monotonic and the other is not, thereby bringing students under the concept of an invertible function.

The teacher then formulates the definition of an invertible function and proves the invertible function theorem using the monotonic function graph on the interactive whiteboard.
Definition 1: The function y=f(x), x X is called reversible, if it takes any of its values only at one point of the set X.
Theorem: If the function y=f(x) is monotone on the set X , then it is invertible.
Proof:
- Let the function y=f(x) increases by X let it go x 1 ≠ x 2- two points of the set X.
- For definiteness, let x 1<
x 2.
Then from what x 1< x 2 follows that f(x 1) < f(x 2). - Thus, different values of the argument correspond to different values of the function, i.e. the function is reversible.

(During the proof of the theorem, the teacher makes all the necessary explanations on the drawing with a marker)
Before formulating the definition of an inverse function, the teacher asks students to determine which of the proposed functions is reversible? The interactive whiteboard shows graphs of functions and several analytically defined functions are written:
B) 
G) y = 2x + 5
D) y = -x 2 + 7
The teacher introduces the definition of an inverse function.
Definition 2: Let an invertible function y=f(x) defined on the set X And E(f)=Y. Let's match each y from Y then the only meaning X, at which f(x)=y. Then we get a function that is defined on Y, A X is the range of the function
This function is denoted x=f -1 (y) and is called the inverse of the function y=f(x).
Students are invited to draw a conclusion about the relationship between the domain of definition and the set of values of inverse functions.
To consider the question of how to find the inverse function of a given, the teacher involved two students. The day before, the children received a task from the teacher to independently analyze the analytical and graphical methods for finding the inverse given function. The teacher acted as a consultant in preparing students for the lesson.
Message from the first student.
Note: the monotonicity of a function is sufficient condition for the existence of an inverse function. But it is not necessary condition.
The student gave examples of various situations when the function is not monotonic, but reversible, when the function is not monotonic and not reversible, when it is monotonic and reversible

Then the student introduces students to the method of finding the inverse function given analytically.
Finding algorithm
- Make sure the function is monotonic.
- Express x in terms of y.
- Rename variables. Instead of x \u003d f -1 (y) they write y \u003d f -1 (x)
Then solves two examples to find the function of the inverse of the given.
Example 1: Show that there is an inverse function for the function y=5x-3 and find its analytical expression.
Solution. The linear function y=5x-3 is defined on R, increases on R, and its range is R. Hence, the inverse function exists on R. To find its analytical expression, we solve the equation y=5x-3 with respect to x; we get This is the desired inverse function. It is defined and increases by R.
Example 2: Show that there is an inverse function for the function y=x 2 , x≤0, and find its analytical expression.

The function is continuous, monotone in its domain of definition, therefore, it is invertible. Having analyzed the domains of definition and the set of values of the function, a corresponding conclusion is made about the analytical expression for the inverse function.
The second student makes a presentation about graphic how to find the inverse function. In the course of his explanation, the student uses the capabilities of the interactive whiteboard.
To get the graph of the function y=f -1 (x), inverse to the function y=f(x), it is necessary to transform the graph of the function y=f(x) symmetrically with respect to the straight line y=x.
During the explanation on the interactive whiteboard, the following task is performed:
Construct a graph of a function and a graph of its inverse function in the same coordinate system. Write down an analytical expression for the inverse function.
4. Primary fixation of the new material.
Target - to establish the correctness and awareness of the understanding of the studied material, to identify gaps in the primary understanding of the material, to correct them.
Students are divided into pairs. They are given sheets with tasks in which they work in pairs. Time to complete the work is limited (5-7 minutes). One pair of students works on the computer, the projector is turned off for this time and the rest of the children cannot see how the students work on the computer.
At the end of the time (it is assumed that the majority of students completed the work), the interactive whiteboard (the projector turns on again) shows the work of the students, where it is clarified during the test that the task was completed in pairs. If necessary, the teacher conducts corrective, explanatory work.
Independent work in pairs<Appendix 2 >
5. The result of the lesson. On the questions that were asked before the lecture. Announcement of grades for the lesson.
Homework §10. №№ 10.6(а,c) 10.8-10.9(b) 10.12(b)
Algebra and the beginnings of analysis. Grade 10 In 2 parts for educational institutions (profile level) / A.G. Mordkovich, L.O. Denishcheva, T.A. Koreshkova and others; ed. A.G. Mordkovich, M: Mnemosyne, 2007



