Seno 2 en el círculo numérico. Ecuación sen x = a. Entrenamos para encontrar los valores de seno y coseno en un círculo

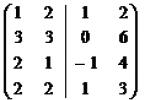
Ejercicio.
Encuentre el valor de x en .

Solución.
Encontrar el valor del argumento de la función, en el que es igual a algún valor, significa determinar para qué argumentos el valor del seno será exactamente el mismo que se indica en la condición.
En este caso, debemos averiguar en qué valores el valor del seno será igual a 1/2. Esto se puede hacer de varias maneras.
Por ejemplo, use , para determinar en qué valores de x la función seno será igual a 1/2.
Otra forma es usar . Déjame recordarte que los valores de los senos se encuentran en el eje Oy.
La forma más común es usar , especialmente cuando se trata de valores estándar para esta función como 1/2.
En todos los casos, uno no debe olvidarse de una de las propiedades más importantes del seno: su período.
Encontremos el valor 1/2 para el seno en la tabla y veamos qué argumentos le corresponden. Los argumentos que nos interesan son Pi/6 y 5Pi/6.
Escriba todas las raíces que satisfagan la ecuación dada. Para hacer esto, escribimos el argumento desconocido x que nos interesa y uno de los valores del argumento obtenido de la tabla, es decir, Pi / 6. Escribamos para ello, teniendo en cuenta el período sinusoidal, todos los valores del argumento:

Tomemos el segundo valor y sigamos los mismos pasos que en el caso anterior:

La solución completa de la ecuación original será:
Y
q puede tomar el valor de cualquier entero.

En un círculo trigonométrico, además de ángulos en grados, observamos.

Más sobre radianes:

Un radián se define como el valor angular de un arco cuya longitud es igual a su radio. En consecuencia, dado que la circunferencia es , entonces es obvio que el radian cabe en el circulo, es decir

1 rad ≈ 57,295779513° ≈ 57°17′44,806″ ≈ 206265″.

Todo el mundo sabe que un radián es

Así, por ejemplo, , un . así es como nosotros Aprende a convertir radianes a ángulos.

Ahora viceversa vamos a convertir grados a radianes.

Digamos que necesitamos convertir a radianes. nos ayudará Procedemos de la siguiente manera:

Dado que, radianes, entonces completa la tabla:

Entrenamos para encontrar los valores de seno y coseno en un círculo

Aclaremos lo siguiente.

Bueno, es bueno si se nos pide que calculemos, por ejemplo, generalmente no hay confusión aquí, todos comienzan a mirar primero en el círculo.

Y si les piden que calculen, por ejemplo,... Muchos, de repente, empiezan a no entender dónde buscar ese cero... Muchas veces lo buscan en el origen. ¿Por qué?

1) ¡Pongámonos de acuerdo de una vez por todas! Lo que viene después o es argumento=ángulo, y nuestros rincones son en el círculo, ¡no los busques en el eje x!(Es solo que los puntos individuales caen tanto en el círculo como en el eje ...) Y los valores de los senos y cosenos en sí mismos, ¡los estamos buscando en los ejes!

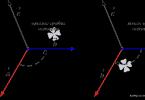
2) ¡Y más! Si partimos del punto de partida en sentido anti-horario(la dirección principal de pasar por alto el círculo trigonométrico), luego apartamos los valores positivos de los ángulos, los ángulos aumentan a medida que nos movemos en esa dirección.

Si partimos del punto de partida en el sentido de las agujas del reloj, luego apartamos los valores negativos de los ángulos.

Ejemplo 1

Encuentra valor.

Solución:

Nos encontramos en el círculo. Proyectamos el punto sobre el eje del seno (es decir, dibujamos una perpendicular desde el punto hasta el eje del seno (oy)).

Llegamos a 0. Por lo tanto, .

Ejemplo 2

Encuentra valor.

Solución:

Nos encontramos en el círculo (pasamos en sentido antihorario y más). Proyectamos un punto sobre el eje del seno (y ya se encuentra en el eje del seno).

Caemos en -1 a lo largo del eje del seno.

Tenga en cuenta que detrás del punto "oculto" hay puntos como (podríamos ir al punto marcado como , en el sentido de las agujas del reloj, lo que significa que aparece un signo menos), e infinidad de otros.

Se puede hacer la siguiente analogía:

Imagina un círculo trigonométrico como una cinta de correr de un estadio.

Después de todo, puedes terminar en el punto "Bandera", empiezo en sentido contrario a las agujas del reloj, corriendo, digamos, 300 m o corriendo, digamos, 100 m en el sentido de las agujas del reloj (consideramos que la longitud de la pista es de 400 m).

Y también puede terminar en el punto de "Bandera" (después de "inicio") corriendo, digamos, 700 m, 1100 m, 1500 m, etc. en sentido contrario a las agujas del reloj. Puede llegar al Flag Point corriendo 500 m o 900 m, etc. en el sentido de las agujas del reloj desde el principio.

Expanda mentalmente la cinta de correr del estadio en una recta numérica. Imagina dónde en esta línea estarán, por ejemplo, los valores 300, 700, 1100, 1500, etc. Veremos puntos en la recta numérica, equidistantes entre sí. Demos la vuelta. Los puntos se "pegan juntos" en uno.

Lo mismo ocurre con el círculo trigonométrico. Detrás de cada punto hay infinitos otros.

Digamos ángulos , , , etc. se muestra como un solo punto. Y los valores del seno, coseno en ellos, por supuesto, son los mismos. (¿Notaste que sumamos/restamos o? Este es el período para la función de seno y coseno).

Ejemplo 3

Encuentra valor.

Solución:

Vamos a convertir a grados por simplicidad.

(luego, cuando te acostumbres al círculo trigonométrico, no necesitarás convertir radianes a grados):

Nos moveremos en el sentido de las agujas del reloj desde el punto Vamos medio círculo () y más

Entendemos que el valor del seno coincide con el valor del seno y es igual a

Tenga en cuenta que si tomamos, por ejemplo, o, etc., obtendríamos el mismo valor del seno.

Ejemplo 4

Encuentra valor.

Solución:

Sin embargo, no convertiremos radianes a grados, como en el ejemplo anterior.

Es decir, tenemos que ir en sentido contrario a las agujas del reloj medio círculo y otro cuarto de medio círculo y proyectar el punto resultante en el eje del coseno (eje horizontal).

Ejemplo 5

Encuentra valor.

Solución:

¿Cómo trazar en un círculo trigonométrico?

Si pasamos o, sí, al menos, terminaremos igual en el punto que designamos como “inicio”. Por lo tanto, puede ir inmediatamente a un punto en el círculo.

Ejemplo 6

Encuentra valor.

Solución:

Terminaremos en un punto (nos llevará de todos modos al punto cero). Proyectamos el punto del círculo sobre el eje del coseno (ver el círculo trigonométrico), entramos. Eso es .

Círculo trigonométrico - en tus manos

Ya entendiste que lo principal es recordar los valores de las funciones trigonométricas del primer trimestre. En los cuartos restantes, todo es similar, solo debes seguir las indicaciones. Y espero que no olvide la "escalera de cadena" de los valores de las funciones trigonométricas.

Como encontrar valores de tangente y cotangenteángulos principales.

Después de eso, habiéndose familiarizado con los valores básicos de la tangente y la cotangente, puedes pasar

En una plantilla de círculo vacío. ¡Tren!

Los valores del seno están en el rango [-1; 1], es decir -1 ≤ sen α ≤ 1. Por lo tanto, si |a| > 1, entonces la ecuación sen x = a no tiene raíces. Por ejemplo, la ecuación sen x = 2 no tiene raíces.

Pasemos a algunas tareas.

Resuelve la ecuación sen x = 1/2.

Solución.

Tenga en cuenta que sen x es la ordenada del punto del círculo unitario, que se obtiene como resultado de la rotación del punto Р (1; 0) por el ángulo x alrededor del origen.

Una ordenada igual a ½ está presente en dos puntos del círculo M 1 y M 2.

Dado que 1/2 \u003d sin π / 6, entonces el punto M 1 se obtiene del punto P (1; 0) girando a través del ángulo x 1 \u003d π / 6, así como a través de los ángulos x \u003d π / 6 + 2πk, donde k \u003d +/-1, +/-2, …

El punto M 2 se obtiene del punto P (1; 0) como resultado de girar el ángulo x 2 = 5π/6, así como los ángulos x = 5π/6 + 2πk, donde k = +/- 1, +/-2, ... , es decir en ángulos x = π – π/6 + 2πk, donde k = +/-1, +/-2, ….

Entonces, todas las raíces de la ecuación sen x = 1/2 se pueden encontrar mediante las fórmulas x = π/6 + 2πk, x = π - π/6 + 2πk, donde k € Z.

Estas fórmulas se pueden combinar en una: x \u003d (-1) n π / 6 + πn, donde n € Z (1).

De hecho, si n es un número par, es decir, n = 2k, luego de la fórmula (1) obtenemos х = π/6 + 2πk, y si n es un número impar, es decir n = 2k + 1, luego de la fórmula (1) obtenemos х = π – π/6 + 2πk.

Respuesta. x \u003d (-1) n π / 6 + πn, donde n € Z.

Resuelve la ecuación sen x = -1/2.

Solución.

La ordenada -1/2 tiene dos puntos del círculo unitario M 1 y M 2, donde x 1 = -π/6, x 2 = -5π/6. Por lo tanto, todas las raíces de la ecuación sin x = -1/2 se pueden encontrar mediante las fórmulas x = -π/6 + 2πk, x = -5π/6 + 2πk, k ∈ Z.

Podemos combinar estas fórmulas en una: x \u003d (-1) n (-π / 6) + πn, n € Z (2).

De hecho, si n = 2k, entonces por la fórmula (2) obtenemos x = -π/6 + 2πk, y si n = 2k – 1, entonces por la fórmula (2) encontramos x = -5π/6 + 2πk.

Respuesta. x \u003d (-1) n (-π / 6) + πn, n € Z.

Así, cada una de las ecuaciones sen x = 1/2 y sen x = -1/2 tiene un número infinito de raíces.

En el segmento -π/2 ≤ x ≤ π/2, cada una de estas ecuaciones tiene una sola raíz:
x 1 \u003d π / 6 - la raíz de la ecuación sin x \u003d 1/2 y x 1 \u003d -π / 6 - la raíz de la ecuación sin x \u003d -1/2.

El número π/6 se llama arcoseno del número 1/2 y se escribe: arcsen 1/2 = π/6; al número -π/6 se le llama arcoseno del número -1/2 y se escribe: arcsen (-1/2) = -π/6.

En general, la ecuación sen x \u003d a, donde -1 ≤ a ≤ 1, en el segmento -π / 2 ≤ x ≤ π / 2 tiene una sola raíz. Si a ≥ 0, entonces la raíz está encerrada en el intervalo; si un< 0, то в промежутке [-π/2; 0). Этот корень называют арксинусом числа а и обозначают arcsin а.

Así, el arcoseno del número a € [–1; 1] tal número se llama € [–π/2; π/2], cuyo seno es a.

arcsen a = α si sen α = a y -π/2 ≤ x ≤ π/2 (3).

Por ejemplo, arcsen √2/2 = π/4, ya que sen π/4 = √2/2 y – π/2 ≤ π/4 ≤ π/2;
arcsen (-√3/2) = -π/3, ya que sen (-π/3) = -√3/2 y – π/2 ≤ – π/3 ≤ π/2.

De manera similar a como se hizo al resolver los problemas 1 y 2, se puede demostrar que las raíces de la ecuación sen x = a, donde |a| ≤ 1 se expresan mediante la fórmula

x \u003d (-1) n arcsin a + πn, n € Z (4).

También podemos probar que para cualquier a € [-1; 1] la fórmula arcsen (-a) = -arcsen a es válida.

De la fórmula (4) se sigue que las raíces de la ecuación
sin x \u003d a para a \u003d 0, a \u003d 1, a \u003d -1 se puede encontrar usando fórmulas más simples:

sin x \u003d 0 x \u003d πn, n € Z (5)

sin x \u003d 1 x \u003d π / 2 + 2πn, n € Z (6)

sin x \u003d -1 x \u003d -π / 2 + 2πn, n € Z (7)

sitio, con copia total o parcial del material, se requiere un enlace a la fuente.

Solución de las ecuaciones trigonométricas más sencillas.

La solución de ecuaciones trigonométricas de cualquier nivel de complejidad finalmente se reduce a resolver las ecuaciones trigonométricas más simples. Y en esto, el círculo trigonométrico nuevamente resulta ser el mejor ayudante.

Recuerda las definiciones de coseno y seno.

El coseno de un ángulo es la abscisa (es decir, la coordenada a lo largo del eje) de un punto en el círculo unitario correspondiente a la rotación de un ángulo dado.

El seno de un ángulo es la ordenada (es decir, la coordenada a lo largo del eje) de un punto en el círculo unitario correspondiente a la rotación de un ángulo dado.

La dirección positiva del movimiento a lo largo del círculo trigonométrico se considera un movimiento en sentido antihorario. Una rotación de 0 grados (o 0 radianes) corresponde a un punto con coordenadas (1; 0)

Usamos estas definiciones para resolver las ecuaciones trigonométricas más simples.

1. Resuelve la ecuación

Esta ecuación se cumple con todos esos valores del ángulo de rotación, que corresponden a los puntos del círculo, cuya ordenada es igual a.

Marcamos un punto con ordenada en el eje y:

Dibuja una línea horizontal paralela al eje x hasta que se cruce con el círculo. Obtendremos dos puntos que se encuentran en un círculo y tienen una ordenada. Estos puntos corresponden a ángulos de rotación de y radianes:

Si, habiendo dejado el punto correspondiente al ángulo de rotación por radianes, damos una vuelta completa, llegaremos a un punto correspondiente al ángulo de rotación por radianes y que tiene la misma ordenada. Es decir, este ángulo de rotación también satisface nuestra ecuación. Podemos hacer tantos giros "inactivos" como queramos, volviendo al mismo punto, y todos estos valores de ángulo satisfarán nuestra ecuación. El número de revoluciones "inactivas" se indica con la letra (o). Como podemos hacer estas revoluciones tanto en dirección positiva como negativa, (o ) puede tomar cualquier valor entero.

Es decir, la primera serie de soluciones a la ecuación original tiene la forma:

, , - conjunto de enteros (1)

De manera similar, la segunda serie de soluciones tiene la forma:

, Dónde , . (2)

Como habrás adivinado, esta serie de soluciones se basa en el punto del círculo correspondiente al ángulo de rotación por .

Estas dos series de soluciones se pueden combinar en una entrada:

Si tomamos esta entrada (es decir, incluso), obtendremos la primera serie de soluciones.

Si tomamos esta entrada (es decir, impar), obtendremos la segunda serie de soluciones.

2. Ahora resolvamos la ecuación

Como es la abscisa del punto del círculo unitario obtenido al girar el ángulo , marcamos en el eje un punto con la abscisa :

Dibuja una línea vertical paralela al eje hasta que se cruce con el círculo. Obtendremos dos puntos que se encuentran sobre un círculo y que tienen una abscisa. Estos puntos corresponden a ángulos de rotación de y radianes. Recuerde que cuando nos movemos en el sentido de las agujas del reloj, obtenemos un ángulo de rotación negativo:

Anotamos dos series de soluciones:

(Llegamos al punto correcto pasando desde el círculo completo principal, es decir.

Combinemos estas dos series en una publicación:

3. Resuelve la ecuación

La recta de tangentes pasa por el punto de coordenadas (1,0) de la circunferencia unitaria paralela al eje OY

Marque un punto en él con una ordenada igual a 1 (buscamos la tangente cuyos ángulos son 1):

Conecte este punto al origen con una línea recta y marque los puntos de intersección de la línea con el círculo unitario. Los puntos de intersección de la línea y el círculo corresponden a los ángulos de rotación en y :

Dado que los puntos correspondientes a los ángulos de rotación que satisfacen nuestra ecuación están separados por radianes, podemos escribir la solución de la siguiente manera:

4. Resuelve la ecuación

La línea de cotangentes pasa por el punto con las coordenadas del círculo unitario paralelas al eje.

Marcamos un punto con la abscisa -1 en la recta de cotangentes:

Conecte este punto al origen de la línea recta y continúe hasta que se cruce con el círculo. Esta línea cortará el círculo en puntos correspondientes a ángulos de rotación de y radianes:

Como estos puntos están separados entre sí por una distancia igual a , entonces podemos escribir la solución general de esta ecuación de la siguiente manera:

En los ejemplos dados, que ilustran la solución de las ecuaciones trigonométricas más simples, se utilizaron valores tabulares de funciones trigonométricas.

Sin embargo, si hay un valor que no está en la tabla en el lado derecho de la ecuación, sustituimos el valor en la solución general de la ecuación: