prepis

1 MINISTRSTVO ZA IZOBRAŽEVANJE IN ZNANOST RUSKE FEDERACIJE Zvezna državna proračunska izobraževalna ustanova za visoko šolstvo "Togliatti State University" Inštitut za matematiko, fiziko in informacijske tehnologije Oddelek "Algebra in geometrija" L A V R S K A Y A B O T A Smer priprave diplomanta: Pedagoško izobraževanje Usmeritev (profil ): Matematika in računalništvo Študent V.V. Nazarov Znanstveni mentor: dr., prof. R.A. Uteeva Sprejem za zagovor Vodja oddelka: doktor pedagoških znanosti, prof. R.A. Uteeva 016 Togliatti - 016

2 VSEBINA UVOD... POGLAVJE I. METODIČNI SISTEM POUČEVANJA TEME "KVADRATNI KORENI" PRI TEČAJU ALGEBRE OSNOVNE ŠOLE Glavni cilji in cilji poučevanja teme "Kvadratni koreni" pri predmetu algebra osnovne šole šole Oblike, metode in sredstva poučevanja teme "Kvadratni koreni" v tečaju algebre osnovne šole ... 5 Zaključek o poglavju I ... POGLAVJE II. METODIČNA PRIPOROČILA ZA ORGANIZACIJO POUKA TEME "KVADRATNI KORENI" V PREDMETU ALGEBRE OSNOVNE ŠOLE Naloge na temo "Kvadratni koreni", osredotočene na osnovno raven znanja in spretnosti pri predmetu algebre glavne šole Naloge na temo "Kvadratni koreni", osredotočen na pripravo na zaključno spričevalo in opravljanje OGE iz matematike Zaključek o poglavju II ZAKLJUČEK SEZNAM UPORABLJENE LITERATURE ... 58

3 UVOD Relevantnost študije. Tema "Kvadratni koreni" je ena od tradicionalnih tem tečaja šolske algebre v osnovni šoli. Njeno preučevanje števil, pridobljenih v letu, temelji na znanju in veščinah učencev o racionalnem poteku matematike v 6. razredu. Izboljšanje veščin izvajanja operacij na racionalnih številih se pojavlja v tečaju algebre 7. razreda. Pomen in mesto preučevanja teme "Kvadratni koreni" v tečaju algebre 8. razreda je povezano s potrebo po nadaljnji razširitvi nabora racionalnih števil in uvedbi iracionalnih števil. Dobro znani praktični problem iskanja strani (dolžine stranice) kvadrata glede na njegovo dano površino lahko služi kot motivacija za preučevanje teme, za rešitev katere prej znana števila niso dovolj. Poleg tega je pri reševanju številnih geometrijskih problemov, problemov v fiziki, kemiji in biologiji potrebno rešiti enačbe, ki vsebujejo kvadratne korenine. Zato je pomembno poznati pravila delovanja s kvadratnimi koreni in se naučiti transformirati izraze, ki jih vsebujejo. Obrnemo se na zgodovino koncepta kvadratnega korena in njegove oznake, sestavljene na podlagi naslednjih virov. n Sodobna oblika znaka kvadratnega korena za x in x se ni pojavila takoj. Razvoj radikalnega predznaka je trajal skoraj pet stoletij, začenši s 13. stol., ko so italijanski in nekateri evropski matematiki kvadratni koren prvi poimenovali z latinsko besedo Radix (koren) ali skrajšano R. V 15. st. N. Schücke je zapisal R 1 namesto 1. Sodobni korenski znak je nastal iz označbe, ki so jo uporabljali nemški matematiki 15.-16. stoletja, ki so algebro imenovali "Kossova znanost", matematiki-algebraisti pa "kossists". (Matematiki 12.-15. stoletja so vsa svoja dela pisali izključno v latinščini. Neznano so imenovali res (stvar).

4 Italijanski matematiki so besedo res prevedli kot cosa. Zadnji izraz so si izposodili Nemci, od katerih sta se pojavila kossists in koss.) V 15. st. nekateri nemški kosisti so uporabljali piko pred izrazom ali številom za označevanje kvadratnega korena. V kurzivnem pisanju so te pike nadomestile pomišljaje, kasneje pa so se spremenile v simbol Eden takih znakov je pomenil običajen kvadratni koren. Če je bilo treba označiti koren četrte stopnje, je bil uporabljen dvojni znak. Ostaja le ugibati, kako natančno je bil označen koren osme stopnje. Če vzamemo analogijo s četrto stopnjo, potem naj bi ta znak identificiral trikratno ekstrakcijo kvadratnega korena, torej za to je bilo potrebno postaviti tri kvadrate. Vendar je ta zapis vzet s kubičnim korenom. Najverjetneje je pozneje iz takšnih oznak nastal znak V, pisno blizu sodobnemu znaku, ki ga poznajo šolarji, vendar brez zgornje črte. Prvič je bil ta znak viden v nemški algebri "Lepo in hitro štetje s pomočjo spretnih pravil algebre." Avtor tega dela je bil učitelj matematike z Dunaja, po rodu iz Češke, Krishtof Rudolf. Knjiga je doživela velik uspeh in je bila v 16. stoletju nenehno ponatisnjena. in potem vse do 1615. Znak korena, ki ga je predlagal Krishtof, sta uporabila A. Girard, S. Stevin (korenski eksponent je zapisal desno od radikalnega znaka v krogu: V () ali V (). Leta 166 je nizozemski matematik A. Girard je spremenil znak Rudolfovega korena in uvedel zelo blizu sodobnemu označevanju.Ta oblika pisanja je začela nadomeščati prejšnji znak R. Vendar je bil nekaj časa korenski znak napisan prek zgornje črte, in sicer: a + b. In šele leta 167 je Rene Descartes vodoravno črto povezal s kljukico, pri čemer je v svoji knjigi "Geometrija" uporabil novo oznako. Toda tudi tukaj ni bilo natančne kopije sodobne oblike. Descartesov zapis je bil nekoliko drugačen od tistega smo vajeni, v eni podrobnosti Ima 4

5 je bilo zapisano: C + 1 q qq p, kjer je črka C, postavljena takoj za radikalom, označevala zapis kubičnega korena. V sodobni obliki bi ta izraz izgledal takole: C + 1 q q p. Najbližje sodobnemu črkovanju radikala je uporabil Newton v svoji "Univerzalni aritmetiki" (1685). Le nekaj časa po njegovem pisanju so matematiki planeta končno sprejeli enotno in dokončno obliko zapisovanja kvadratnega korena. Raziskovalni problem: kakšne so metodološke značilnosti poučevanja teme "Kvadratni koreni" v šoli? 5 pri predmetu algebra 8. razreda glavni Predmet raziskave je proces poučevanja algebre za učence osnovne šole. Predmet raziskave je metodični sistem poučevanja teme "Kvadratni koreni". Namen diplomskega dela je razkriti metodološki sistem poučevanja teme "Kvadratni koreni". Cilji raziskave: 1. Ugotoviti glavne cilje in cilje poučevanja teme "Kvadratni koreni" v tečaju algebre glavne šole (ciljna komponenta metodološkega sistema). različne oblike, metode in sredstva poučevanja teme " Kvadratni koreni" pri predmetu algebra glavne šole (organizacijski

6 sestavin metodološkega sistema). 4. Oblikujte metodološka priporočila za poučevanje teme "Kvadratni koreni". Raziskovalne metode: analiza znanstvene in metodološke literature, programov iz matematike, šolskih učbenikov o algebri na temo raziskovanja, analiza, sistematizacija in posploševanje gradiva. Praktični pomen tega dela je v tem, da predstavlja metodološki sistem za poučevanje teme "Kvadratni koreni" v tečaju algebre glavne šole in oblikuje metodološka priporočila, ki jih lahko uporabljajo učitelji matematike, pa tudi diplomanti med študijem. obdobje pedagoške prakse na šoli. Predstavljeni rezultati in zaključki diplomskega dela se lahko uporabijo kot osnova za nadaljnji razvoj metodologije za poučevanje študentov teme "Kvadratni koreni". Za zagovor je predložen: metodološki sistem za poučevanje teme "Kvadratni koreni" v tečaju algebre glavne šole. Struktura dela. Diplomsko delo je sestavljeno iz uvoda, dveh poglavij, zaključka, seznama referenc. 6

7 POGLAVJE I. METODIČNI SISTEM POUČEVANJA TEME "KVADRATNI KORENI" V TEČAJU ALGEBRE OSNOVNE ŠOLE 1. Glavni cilji in cilji poučevanja teme "Kvadratni koreni" v tečaju algebre glavnega šolskega predmetnega področja " Matematika" mora zagotoviti: 1) oblikovanje idej o matematiki kot metodi spoznavanja resničnosti, ki vam omogoča opisovanje in preučevanje resničnih procesov in pojavov;) razvoj spretnosti za delo z izobraževalnim matematičnim besedilom (analizirajte, izločite potrebne podatke), natančno in kompetentno izraža svoje misli z matematično terminologijo in simboliko, izvaja klasifikacije, racionalizacije, dokaze matematičnih trditev;) razvijanje predstav o številu in številskih sistemih od naravnih do realnih števil; obvladovanje veščin ustnega, pisnega, instrumentalnega računanja; 4) obvladovanje simbolnega jezika algebre, metod za izvajanje identičnih transformacij izrazov, reševanje enačb, sistemov enačb, neenačb in sistemov neenačb; sposobnost modeliranja realnih situacij v jeziku algebre, raziskovanja konstruiranih modelov z uporabo aparata algebre, interpretacije rezultata; V programu matematike avtor opredeljuje naslednje cilje in cilje za preučevanje teme "Kvadratni koreni": Razširitev nabora racionalnih števil, uvedba koncepta iracionalnih in realnih števil, preučevanje kvadratnih korenov in dejanj z njimi. 7

8 Kot rezultat preučevanja teme morajo študenti vedeti: 1. Definicija periodičnih in neperiodičnih neskončnih decimalnih ulomkov .. Funkcija y \u003d x, njene lastnosti in graf .. Koncept kvadratnega korena 4. Lastnosti aritmetični kvadratni koren. 5. Množica realnih, racionalnih in iracionalnih števil. Kot rezultat preučevanja teme morajo učenci znati: 1. Pretvarjati navadne ulomke v decimalne in obratno.. Primerjati realna, racionalna in iracionalna števila.. Znati grafično prikazati funkcijo y=x. 4. Vnesite in odvzemite faktor izpod znaka korena. 5. Izvedite dejanja s kvadratnimi koreni. V matematičnem programu avtor opredeljuje naslednje cilje in cilje za preučevanje teme "Kvadratni koreni" (v učbenik Makarycheva): sistematizirati informacije o racionalnih številih in dati idejo o iracionalnih številih, s čimer se razširi koncept števila; razvijejo sposobnost izvajanja preprostih transformacij izrazov, ki vsebujejo kvadratne korene. Kot rezultat preučevanja teme morajo učenci poznati: 1. Naravna, cela, racionalna, iracionalna in realna števila Modul števila a.. Aritmetični kvadratni koren in njegove lastnosti. 4. Funkcija y= x, njene lastnosti in graf. Kot rezultat preučevanja teme bi študentje morali znati: 1. Reševati najpreprostejše kvadratne enačbe. 8

9. Vnesite in odvzemite faktor izpod znaka korena. Poiščite približne vrednosti kvadratnih korenov. 4. Izlušči kvadratni koren potence števila. 5. Preoblikovanje iracionalnih izrazov. V programu matematike avtor opredeljuje naslednje cilje in cilje za preučevanje teme "Kvadratni koreni" v Alimovem učbeniku: sistematizirati informacije o racionalnih številih in dati idejo o iracionalnih številih, s čimer se razširi koncept števila; razvijejo sposobnost izvajanja preprostih transformacij izrazov, ki vsebujejo kvadratne korene. Kot rezultat preučevanja teme bi morali učenci vedeti: 1. Koncept aritmetičnega kvadratnega korena .. Realna števila Kot rezultat preučevanja teme bi morali biti učenci sposobni najti kvadratni koren stopnje, produkta in ulomka. V članku S. Minaeva [, str. 4-7] je navedeno, da ima študij razdelka "Kvadratne korenine" naslednje cilje: naučiti se izvajati transformacije izrazov, ki vsebujejo kvadratne korenine; na primeru kvadratnega in kubnega korena oblikujejo začetne predstave o korenu n-te stopnje. Zgledni osnovni izobraževalni program osnovne splošne izobrazbe z dne 8. 4. 015 pravi, da se mora maturant v 8. razredu naučiti (za uporabo v vsakdanjem življenju, pri študiju drugih predmetov in zagotavljanje možnosti uspešnega nadaljevanja izobraževanja na osnovni ravni): 1. .Operirajo na osnovni ravni pojmi: naravno število, celo število, navadni ulomek, decimalni ulomek, mešani ulomek, racionalno število, aritmetični kvadratni koren.Oceni vrednost kvadratnega korena pozitivnega celega števila. 9

10. Prepoznajte racionalna in iracionalna števila. 4. Primerjaj števila. 5. Razumeti pomen zapisa števila v standardni obliki. 6. Rešite kvadratne enačbe z uporabo formule korenov kvadratne enačbe. 7. Rešitve neenačb in njihovih sistemov upodabljajo na realni premici. Maturant bo imel možnost, da se v 8. razredu za zagotovitev možnosti uspešnega nadaljevanja izobraževanja na osnovni in nadaljevalni ravni nauči: 1. operirati s pojmi: množica naravnih števil, množica celih števil, množica racionalnih števil, iracionalno število, kvadratni koren, množica realnih števil, geometrijska interpretacija naravnih števil, cela, racionalna, realna števila.. Računati, tudi z metodami racionalnega računanja.. Primerjati racionalna in iracionalna števila. 4. Predstavi racionalno število kot decimalni ulomek. 5. Izvedite transformacije izrazov, ki vsebujejo kvadratne korene. 6. Izberite kvadrat vsote ali razlike binoma v izrazih, ki vsebujejo kvadratne korene Metodološka analiza vsebine poučevanja teme "Kvadratni koreni" v tečaju algebre osnovne šole Basic (znano iz šolskega tečaja matematike 5 -6 algebra 7 razredi) znanje: pojem racionalnega števila; pojem množice racionalnih števil in njen zapis; 10 in seveda

11 osnovnih akcij (operacij) z racionalnimi števili; funkcija y = x. Nova (uvedena) znanja: pojem kvadratnega korena števila; koncept aritmetičnega kvadratnega korena; lastnosti aritmetičnih kvadratnih korenov; vstavljanje in odstranjevanje faktorja izpod znaka korena; dejanja s kvadratnimi koreni. Analiza vsebine teme "Kvadratni koreni" v različnih učbenikih algebre za 8. razred je predstavljena v tabelah 1-4. V učbeniku Yu.N. Makarycheva je več kot v drugih urah namenjena preučevanju razdelka "Kvadratni koreni", celoten del je razdeljen na 4 odstavke. Dotakne se teme proučevanja približnega iskanja kvadratnih korenov, izpuščena pa je tema periodičnih decimalnih ulomkov. V učbeniku G.K. Muravina in O.V. Muravina je razdelku "Kvadratni koreni" namenil nekaj manj kot 18 ur, razdelek je sestavljen iz odstavkov, dotaknjena je tema periodičnih decimalnih ulomkov, vendar ni približne ugotovitve kvadratnih korenov. V učbeniku Nikolskega je razdelek "Kvadratni koreni" sestavljen iz samo enega odstavka in 5 točk, številne teme in koncepti niso predstavljeni. V učbeniku G.V. Dorofejev je vključil temo, posvečeno Pitagorejskemu izreku, ki je ni v vseh zgoraj naštetih. Tu se dotaknemo tudi preučevanja kubičnega korena. V vseh učbenikih se študij razdelka začne z realnimi in iracionalnimi številkami, vendar ima vsak avtor svoj pristop. Nato sledi preučevanje samega kvadratnega korena in aritmetičnega kvadratnega korena, lastnosti in dejanj na njih. enajst

12 Avtorji učbenika Yu.N. Makarychev, N.G. Mindyuk, K.I. Neškov, S.B. Suvorov Naslovi poglavij in odstavkov 4. Realna števila 9. Racionalna števila 10. Iracionalna števila 5. Aritmetični kvadratni koren 11. Kvadratni koreni. Aritmetični kvadratni koren. 1. Enačba x = a. 1. Iskanje približnih vrednosti kvadratnega korena. 14. Funkcija y= x in njen graf. 6. Lastnosti aritmetičnega kvadratnega korena. 15. Kvadratni koren produkta in ulomka. 16. Kvadratni koren potence. 7. Uporaba lastnosti aritmetičnega kvadratnega korena 17. Odstranjevanje faktorja izpod predznaka korena. Vnos množitelja pod znak korena. 18. Pretvorba izrazov s kvadratnimi koreni. Tabela 1 Število ur Skupaj Tabela Avtorji učbenika G.K. Muravin, K.S. Muravin, O.V. Muravina Naslovi poglavij in odstavkov 5. Realna števila 14. Racionalna in iracionalna števila. 15. Periodični in neperiodični neskončni decimalni ulomki. 6. Kvadratni koreni. 16. Funkcija y=x in njen graf. 17. Pojem kvadratnega korena. 18. Lastnosti aritmetičnih kvadratnih korenov. 19. Vstavljanje in odstranjevanje faktorja izpod predznaka korena. 0. Dejanja s kvadratnimi koreni. Število ur Skupaj 18 Tabela Avtorji učbenikov S.M. Nikolski, M.K. Potapov, N.N. Reshetnikov, A.V. Shevkin Naslov poglavij in odstavkov. Kvadratni koren.1 Pojem kvadratnega korena.. Aritmetični kvadratni koren.. Kvadratni koren naravnega števila..4 Približen izračun kvadratnih korenov..5 Lastnosti aritmetičnih kvadratnih korenov. 1

13 Preglednica 4 Avtorji učbenika Naslov poglavij in odstavkov Število ur G.V. Dorofeev .1 Problem iskanja stranice kvadrata. Iracionalna števila. Pitagorov izrek.4 Kvadratni koren (algebrski pristop).5 Lastnosti kvadratnih korenov.6 Transformacija izrazov, ki vsebujejo kvadratne korene.7 Kubični koren Skupaj 18 Preučevanje teme "Kvadratni koreni" na podlagi učbenika algebre za 8. razred avtorjev Muravin. Na začetku je podana razširitev množice racionalnih števil, predstavljena sta pojma iracionalno in realno število, obravnavan je prehod iz navadnega ulomka v decimalni in obratno. Ure so dodeljene za racionalna in iracionalna števila.V odstavku 14. »Racionalna in iracionalna števila« je povedana zgodovina njihovega nastanka in namen preučevanja teme. Definicije so podane na podlagi primerov, razmerij dolžin segmentov. Definicija 1: če imata dva segmenta skupno mero, ki se m-krat prilega enemu segmentu in n-krat drugemu, potem je njuno razmerje m, n racionalno število. Definicija iracionalnega števila je podana v primeru 1: Primer 1: d = (m n) =. Zato je (m n) =. Imenovalec ulomka na levi strani enačbe je drugačen od ena, zato ga je treba zmanjšati za n, da bi bil ulomek enak celemu številu. Toda naravni števili m in n nimata skupnih deliteljev, zato tudi njuni kvadrati nimajo skupnih deliteljev. Torej je enakost m = napačna, tj. število d ni ulomek. n 1

14 Primer je dokazal, da število d ni racionalno število, kar pomeni, da diagonala kvadrata nima skupne mere s svojo stranico, število d je iracionalno število. Naslednji odstavek je posvečen periodičnim in neperiodičnim ulomkom, predstavljen je pojem obdobja in utemeljena je neizogibnost pojava obdobja pri prevodu. Tej točki je posvečen del 1. V odstavku 15 se preučujejo periodični in neperiodični decimalni ulomki, obravnavana je tema iskanja približnega korena za racionalna in iracionalna števila. Nato so na obravnavanih primerih podane definicije končnih in neskončnih decimalnih ulomkov. Primer: Prevedemo 1 v decimalni ulomek, izkaže se: 0, Število, ki se v zapisu neskončno ponavlja, imenujemo obdobje, sam ulomek pa periodični. Lastnost 1: vsako racionalno število lahko predstavimo kot neskončen decimalni periodični ulomek (velja tudi obratno). Definicija: Vsako iracionalno število je zapisano kot neskončen neperiodični decimalni ulomek, vsak neskončen neperiodični decimalni ulomek pa je iracionalno število. Definicija: Neskončna periodična decimalka je racionalno število, neskončna neperiodična decimalka pa je iracionalno število. Po tem je prehod neposredno na študij teme "Kvadratni koreni". Študija se začne z odstavkom "Funkcija y=x in njen graf". Ponavlja se snov o funkcijah in grafih. Določena je ura Najprej se po točkah izriše graf funkcije y=x v kartezičnem koordinatnem sistemu, izvede se njegov študij in poda ime grafa: Definicija 4: graf funkcije y=x se imenuje parabola. 14

15 Prehod na koncept kvadratnega korena se zgodi z rešitvijo kvadratne enačbe x \u003d a, trdi, da nam ta metoda omogoča razlago narave izraza. Ura je razdeljena V naslednjem 17 odstavku je predstavljen koncept kvadratnega korena. Definicija 5: Koreni enačbe x = a se imenujejo kvadratni koreni a. Definicija 6: Nenegativno število, katerega kvadrat je a, imenujemo aritmetični kvadratni koren iz a in ga označimo z a. . Predstavljen je znak radikala in podana je zgodovina njegovega nastanka. Nato avtorji nadaljujejo s preučevanjem lastnosti aritmetičnih kvadratnih korenin, na tej točki se začne razvoj sposobnosti preoblikovanja izrazov s kvadratnimi koreninami. Ure so razdeljene V odstavku 18 so podane lastnosti aritmetičnih kvadratnih korenov: Lastnost: Za poljubno število a a \u003d a. Lastnost: Za poljubni nenegativni števili a in b velja ab= a b . Po tem se preuči in obdela tema uvedbe in odstranitve množitelja izpod znaka korena. Delo se nadaljuje s kvadratnimi koreni. Kot ugotavljajo avtorji, imajo učenci lahko težave pri pretvarjanju dobesednih izrazov, ker je v tej situaciji znak modula bistvenega pomena, ko faktor vzamemo izpod znaka korena. Dodeljen je h V 19. odstavku se preučujeta uvedba in odstranitev faktorja iz načinov predznaka korena, podana je lastnost: Lastnost 4: Za nenegativne vrednosti b a b= a * b= a * b. Nato avtorji preidejo na operacije s kvadratnimi koreni, na tej točki pa se vadijo predvsem v transformaciji številskih izrazov, 15

Svoje znanje na to temo poglablja 16 dijakov. Študij lahko razdelimo na dva dela: 1. Delo s kvadratnimi koreni števil .. Pretvarjanje dobesednih izrazov. Tak študijski model ne določa zaporedja študija, lahko rečemo, da drugi del, čeprav uporaben na tej stopnji, še vedno izvaja propedevtiko snovi 9. razreda, kjer se bo posebej proučevalo preoblikovanje dobesednih izrazov s koreni. Dodeljene 4 ure. V 0 in zadnjem delu se preučujejo dejanja s kvadratnimi koreni. Prejšnje preučene lastnosti se spomnijo in uporabijo pri transformaciji številskih izrazov. Takšna dejanja se štejejo kot: osvoboditev od iracionalnosti v imenovalcu, faktorizacija, poenostavitev izraza. Skupaj avtorji namenijo 19 ur za študij razdelka, po vsakem razdelku je preverjanje ali samostojno delo, na koncu poglavja je test. Preučevanje teme "Kvadratni koreni" na podlagi učbenika algebre za 8. razred avtorja Yu.N. Makarychev. Preučevanje poglavja "Kvadratni koreni" se začne s ponavljanjem realnih števil. Najprej sledi opomnitev na osnovne informacije o množici naravnih števil, deljivosti naravnih števil in obravnava tipičnih nalog na temo. Odmerjena je ena ura, nato ena lekcija za ponovitev osnovnih informacij o celih številih in obravnavo tipičnih problemov, nato pa lekcija o množici racionalnih števil. Sledi učna ura, v kateri je podan pojem iracionalnih števil in množica realnih števil. Po opravljenem zgoraj omenjenem pouku, 16

17 neposrednega študija kvadratnih korenov je lekcija posvečena konceptom kvadratnega korena in aritmetičnega kvadratnega korena. Nato so lekcije namenjene reševanju najpreprostejših kvadratnih enačb x \u003d a in nato 1 lekcija, ki preučuje iskanje približnih vrednosti kvadratnih korenin. Naslednje lekcije so namenjene obravnavi funkcije y= x, njenih lastnosti in grafa. Sledijo lekcije, ki jih je mogoče pripisati lastnostim aritmetičnega kvadratnega korena. V 1. lekciji obravnavamo lastnosti kvadratnega korena zmnožka in ulomka, naslednja lekcija je izločanje kvadratnega korena iz potence števila. Na tej stopnji avtor predlaga, da nekaj lekcij posvetimo kontrolnemu delu in njegovemu preverjanju, nato pa preidemo na lekcije, ki se nanašajo na uporabo lastnosti aritmetičnega kvadratnega korena. 1 lekcija za ponavljanje in vadbo veščin dodajanja in odvzemanja množitelja izpod korena. Nato lekcija, ki obravnava osnovne tehnike za preoblikovanje iracionalnih izrazov. Na koncu avtor predlaga izvedbo končnega testa na temo "Kvadratni koreni". Skupaj je za študij tega razdelka namenjena ena ura. In zdaj razmislimo o priporočilih S. Minaeve o uvedbi koncepta kvadratnega korena pri pouku algebre po učbeniku G.V. Dorofejev v 8. razredu: 1. Problem iskanja strani kvadrata (lekcija) Za uvedbo koncepta kvadratnega korena se uporablja smiseln pristop, ki je značilen za ta tečaj, pri čemer je poudarjen motivacijski in pomenski vidik. Snov je predstavljena na naslednji način: učenci poznajo formulo S = a, s pomočjo katere lahko ob stranici kvadrata a izračunamo njegovo ploščino S; toda v matematiki obstaja formula za reševanje obratnega problema iskanja stranice kvadrata a glede na 17

18 danega območja S, ki je zapisano takole: a \u003d S. Simbol S označuje stran kvadrata, katerega površina je enaka S. Če je na primer S \u003d 100, nato \u003d 100. Od 100 \u003d 10, nato \u003d 100 \u003d 10. Da bi se učenci naučili novega simbola, je mogoče ponuditi več vprašanj tipa: naj območje \u200b Kvadrat naj bo velik 81 m2: s simbolom zapišite izraz za stranico tega kvadrata; kakšna je dolžina stranice kvadrata? Če preidemo iz geometrijskega jezika v algebrski, lahko pomen simbola S opišemo takole: S je nenegativno število, katerega kvadrat je enak S. (Konec koncev dolžine ni mogoče izraziti z negativnim številom! ) Tako pridemo do "delovne" formulacije, ki jo bomo uporabili pri iskanju kvadratnih korenov. Učitelja opozorimo na to, kako se bere simbol S: kvadratni koren iz S. Pridevnik "aritmetični" je tukaj odveč, saj na tem mestu v temi delamo samo s pozitivnimi koreni. Vendar bo izraz uporabljen kasneje. Iracionalna števila (lekcija) V tem odstavku lahko ločimo dva vidika: ideološki in praktični. Ideološke leži v prvem seznanjanju z iracionalnimi števili; praktično - pri oblikovanju sposobnosti vrednotenja "neizvlečnih" korenin, da bi našli njihove približne vrednosti tako s pomočjo ocene kot s pomočjo kalkulatorja. Učenci pridejo do potrebe po uvedbi iracionalnih števil kot rezultat obravnave že znanega problema iskanja stranice kvadrata po njegovi ploščini. V učbeniku slika 10 prikazuje dva kvadrata. Eden od njih je enojni, njegova površina je 1 kvadratni meter. enote Drugi kvadrat ima stransko diagonalo prvega, njegova ploščina pa je dvakrat večja. (Dejansko je mali kvadrat sestavljen iz dveh enakih trikotnikov, veliki pa iz štirih takih 18

19 trikotnikov.) Torej je površina velikega kvadrata kvadratna. enote Kolikšna je dolžina stranice tega kvadrata? Označimo ga z a. Z uporabo znaka kvadratnega korena lahko zapišemo, da je a=. Študenti so se doslej ukvarjali le z "izvlečnimi" koreni. Moramo jim dati nekaj minut, da poskusijo izvleči koren tudi v tem primeru, da se prepričamo, da vrednost a \u003d 1 ni dovolj, in če vzamete \u003d, je to že preveč ; bi poskusil izbrati decimalni ulomek in videl, da je 1,4<, а 1,5 >. Nato je podan dokaj preprost dokaz, da ne obstaja ne celo ne delno število, ki bi mu bilo kvadratno enako (str. 7 učbenika). Tako ni racionalnega števila, ki bi natančno izražalo dolžino stranice našega kvadrata. Želel bi, da bi učenci spoznali neverjetno odkritje, do katerega so prišli matematiki antike (obstaja segment, vendar nima dolžine!), In tudi, da je to dejstvo dalo zagon razvoju matematike (potrebno je bilo uvesti nova števila !). Učencem povemo, da število, ki izraža dolžino stranice kvadrata, katerega ploščina je kvadratna. enota, spada v razred tako imenovanih iracionalnih števil: - to je pozitivno iracionalno število, katerega kvadrat je enak, to je enakost () \u003d velja. Morajo biti sposobni poimenovati druga iracionalna števila oblike a in izvajati transformacije, kot je (a) = a za specifične pozitivne vrednosti a in v obe smeri. Torej je prvo spoznavanje iracionalnih števil podvrženo precej ozkemu cilju: pojavlja se v povezavi s študijem kvadratnih korenin in zagotavlja predvsem potrebe te teme. Poleg zgoraj opisanih podatkov (namreč: med racionalnimi števili ni števila, ki izraža dolžino stranice kvadrata, katerega ploščina je enaka; poleg racionalnih števil obstajajo tudi t.i. iracionalna števila 19)

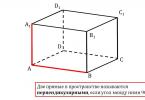
20.; so vsa števila oblike a iracionalna, če a ni kvadrat celega ali delnega števila), učenci spoznajo, da obstaja neskončno veliko iracionalnih števil različne narave (primer je število z), da lahko iracionalna števila negativni in da jih v praksi nadomestijo (približno) decimalni ulomki. Učenci dobijo trdnejše informacije o iracionalnih in realnih številih v "drugem prehodu" v tečaju 9. razreda. Za prikaz temeljne možnosti iskanja decimalne aproksimacije iracionalnega števila oblike a učbenik uporablja metodo vrednotenja: najdejo se približne vrednosti s primanjkljajem in presežkom, izražene kot zaporedna cela števila (to je z natančnostjo od 1), zaporednih decimalnih ulomkov z enim decimalnim mestom (to je do 0,1) itd. Osnova te metode je izjava: če sta a in b pozitivni števili in a

21 V zvezi z uporabo Pitagorovega izreka za računanje dolžine hipotenuze pravokotnega trikotnika po njegovih krakih (primer 1 na str. 84) so ​​v učbeniku omenjene »Pitagorejske trojke«. Upoštevajte, da čeprav jih je neskončno veliko, obstaja samo ena trojka, sestavljena iz zaporednih naravnih števil. Zaželeno je, da konstrukcije odsekov z iracionalnimi dolžinami (ali točk na koordinatni premici z iracionalnimi abscisami) s šestilom in ravnilom ne analiziramo le po besedilu učbenika (str. 85), ampak dejansko dokončamo z vsak učenec v svoj zvezek. Takšno delo se lahko ponudi na primer kot domača naloga. Učence je treba opozoriti, da mora biti risba urejena, dovolj velika in dobro »berljiva«. Analizirali bomo problemsko gradivo v učbenikih in izpostavili glavne vrste problemov, uporabljenih v temi "Kvadratni koreni". Članek izpostavlja vaje na temo "Kvadratni koreni" iz učbenika G.V. Dorofejeva, ki zajema vse bistvene vidike tega uvodnega fragmenta teme. Glavni namen vaj je obvladati nov koncept, razviti sposobnost uporabe radikalnega znaka. Pozornost je namenjena nalogam in 7. Zelo pogosto se zahteva sposobnost premikanja od enakosti oblike a = b do enakosti b = a in obratno. Vaje 8- - izračunati vrednosti številskih in črkovnih izrazov, ki vsebujejo kvadratne korenine. Učenci bi se morali naučiti, da je korenski znak, tako kot oklepaji, simbol združevanja. V vajah 4-7 se naprej razvija že začeto (in z vidika uporabe izjemno pomembno) delo s formulami. Zdaj so to formule, ki vsebujejo radikale ali zahtevajo uporabo radikalov pri izražanju ene spremenljivke z drugimi. Takšne naloge pogosto povzročajo težave študentom, zato jih je mogoče delno dokončati s preučevanjem naslednjih točk. razen 1

22 poleg tega se je koristno vračati k njim. Nalogi 8 in 9 iz skupine B na tej stopnji spadata med težje; Vsekakor niso za vse študente. V razredih z nizko stopnjo priprave lahko opravite naloge skupine A, pa tudi, če je mogoče, 41 in 44. Razmislite o primeru iz učbenika: Poiščite približno vrednost 60. Rešitev: Kvadrat števila je zaprt med dvema "natančnima" kvadratoma - številki 49 in 64: 49<(60), то есть 7 <(60) <8. Значит как 7 <(60), то 7< 60; так как (60) <8, то 60<8. Значит 7< 60<8. Очевидно, что 60 ближе к 8, чем к 7, то есть Рассмотренный способ нахождения приближенного значения корня, в силу своей громоздкости, имеет, в основном, теоретическое значение; учащимся достаточно лишь уметь указывать два целых числа, между которыми заключено значение данного корня. А при решении задач предполагается широкое использование калькулятора. Упражнения к пункту предназначены, прежде всего, для осознанного восприятия этого сложного для учащихся материала (46-51). Кроме того, использование калькулятора позволяет, с помощью наблюдений, прийти к некоторым теоретическим обобщениям, например к выводу о возрастании значения корня с увеличением подкоренного выражения (5-54). В образце к упражнению 6 показаны приемы сравнения, которыми должны овладеть учащиеся. Упражнения 65 и 66 направлены на формирование умения выполнять преобразование выражений, содержащих квадратные корни, с использованием равенства (a) =а, где a 0. В классах с невысоким уровнем подготовки достаточно упражнений группы А. Вообще, в этом блоке дана представительная группа заданий,

23, ki je lahko precej omejena. Vaja 57. Metoda I. S pomočjo kalkulatorja najdemo približne vrednosti korenin: 5,4; 6,45; 7,65. To pomeni, da vsako od teh števil pripada segmentu s koncem v točkah in in se na tem segmentu nahajajo v naslednjem vrstnem redu: 5, 6, 7. Nadalje: število 5 pripada segmentu s koncem v točkah in ,; številka 6 pripada segmentu s koncema v točkah 4 in 5; številka 7 pripada odseku s koncema v točkah 6 in 7. Metoda II. Do enakega rezultata pridemo s pomočjo ocene. Na primer, za 5 imamo:<(5) <, то есть < 5<;, <(5) <, то есть,< 5<,. Упражнение 59. Очевидно, что точке К соответствует число 0,4, так как 0< 0,4< 1. Точно так же легко понять, что число лишнее, так как на отрезке с концами х=1 и х точка не отмечена. Сложнее с точкой L: ведь каждое из оставшихся чисел 5 и 7 располагается на отрезке с концами и. Но точка L расположена в левой половине отрезка, значит число, которое ей соответствует, должно быть меньше,5. Ответ почти очевиден: это 5. Но все же какое-то объяснение необходимо. Можно обратиться к калькулятору, а можно рассуждать так:,5 = 6,5; так как (5) <,5, то 5 <,5. Упражнение 70. а) Сначала находим, что 8< 7,5 < 9, а затем сравниваем числа 8,5 и 7,5. Так как 8,5 = 7,5<7,5, то 8,5< 7,5,

24, kar pomeni, da je število 7,5 bližje 9. Pri reševanju nalog je seveda predvidena uporaba kalkulatorja. V razredih z nizko stopnjo pripravljenosti iz skupine A se lahko omejite na naloge (izpolnjujejo raven obveznih zahtev) in razmislite tudi o raziskovalni nalogi 91. Vaja 86. Naloga je rešena na podlagi slike 7 učbenika . Iz vizualnih premislekov je jasno, da je največja dolžina diagonala paralelepipeda. Primerjaj dolžino diagonale z dolžino jezička. Najprej poiščite dolžino osnovne diagonale l: l= a + b = = 700 (cm). Sedaj poiščemo dolžino diagonale paralelepipeda d: d= (700) + 50 = 9800 (cm). Od 9800< 10000=100, то трость данных размеров поместить в коробку нельзя. Упражнение 90. Геометрически выражение a + b + c можно истолковать как длину диагонали прямоугольного параллелепипеда, измерения которого a, b и с. В самом деле, из прямоугольного треугольника LMN имеем, что LM= a + b. А из прямоугольного треугольника KLN получим, что NM= c + (a + b) = a + b + c По неравенству треугольника a + b + c

25 10= + 1 ; 1= + ; 17= Ampak obstaja še en način. Torej lahko segment dolžine 10 dobimo po naslednjem algoritmu: 10 = (5) + (5). V učbeniku o algebri za 8. razred avtorji Muravine predlagajo začetek študija razdelka z naslednjimi vajami: Vaja 15. Ali gre graf funkcije y \u003d x skozi točko: A (-; 4) B (-, 5; 1) C (; 59) D (-6,5; 4,5). Odgovor: A-da, B-ne C-da D-da. Odstavek 17 ponuja vaje za izračun kvadratnega korena Primer. Izračunaj Do rešitve pride z razgradnjo števila 1105 na prafaktorje. 1105= *5 * = 5 7 = (5 7) =*5*7=105 Odgovor: 105. Točka 18 predstavlja lastnosti aritmetičnih kvadratnih korenov in naloge za njihovo uporabo, poenostavitev radikalnih izrazov in njihovo računanje. Primer 4. (str. 100) Poenostavi (5). (5) = - 5 = 5-. Odgovor: 5-. Primer 5. Izračunajte 0, = 0, =0,8*4*5=80. Odgovor 80. Primer 6. Izračunaj = =4 7. Odgovor: 4 7. V odstavku 19 so obravnavane vaje za dodajanje in odstranjevanje faktorja izpod znaka korena ter težave za primerjavo vrednosti izrazov. 5

26 Primer 7. Izloči faktor izpod korena v izrazu Razstavimo števili 10 in 90 na prafaktorja: 10= **5, 90=* *5. Zato je 10*90= 4 * * = 4 5 = **5* =60. Odgovor: =,5 .. Odgovor:,5. Primer 8. (str. 105) Poenostavi izraz = 5 = 5 = Primer 9. (str. 105) Pod koren vpiši faktor: 5 0,4. 5 0,4 \u003d 5 0,4 \u003d 5 0,4 \u003d 10. Odgovor: 10. Primer 10. (str. 106) Primerjajte vrednosti izrazov in. = 9 = 18 in = 4 = 1. >. Odgovor: >. 0 točk je namenjenih operacijam s kvadratnimi koreni, pretvorbi ulomkov s kvadratnimi koreni, poenostavitvi izrazov, osvoboditvi iracionalnosti. Primer 11. (str. 108) Ulomek 54 pretvorimo tako, da njegov imenovalec ne vsebuje radikala. Odgovor: = 54 = 1 7 = 1 = 4= =. 9 Primer 1. (str. 109) Poenostavite izraz =5 6 96=4 6 = = = =() 6=1 6 Odgovor:

27 Primer 1. (str. 109) Osvobodite ulomek iracionalnosti v imenovalcu. =(). Odgovor: (). 6 = 6(1+ 10) 1 10 (1 10)(1+ 10) =6(1+ 10) = 6(1+ 10) =. Oblike, metode in sredstva poučevanja teme "Kvadratni koreni" v tečaju algebre osnovne šole V tem razdelku bomo analizirali praktične izkušnje pri preučevanju teme na podlagi objavljenih člankov in učnih pripomočkov. V članku S. Minaeve je navedeno, da se koncept kvadratnega korena "pojavi" v predmetu, ki se preučuje, ko razpravljamo o dveh problemih - geometrijskem (o iskanju dolžine stranice kvadrata glede na njegovo ploščino) in algebrskem ( o številu korenov enačbe oblike x = a, kjer je a poljubno število ). V povezavi z obravnavo prve naloge učenci dobijo začetne predstave o iracionalnih številih. V vsebino poglavja je avtor vključil netradicionalno vprašanje za algebro - Pitagorov izrek. To je storjeno za prikaz naravne uporabe kvadratnih korenov za iskanje dolžin segmentov, konstruiranje segmentov z iracionalnimi dolžinami in konstruiranje točk z iracionalnimi koordinatami. Hkrati ni pomembno, kje učenci prvič slišijo za Pitagorov izrek - pri geometriji ali pri algebri. Avtor tudi trdi, da je najpomembnejši rezultat učenja, poleg ideoloških vidikov, sposobnost izvajanja nekaterih transformacij izrazov, ki vsebujejo kvadratne korene (predvsem numerične). Učenci se seznanijo tudi s pojmom kubnega korena; hkrati oblikujejo začetne predstave o korenu 7

28. stopnja. Nazadnje študentje skozi sistem vaj dobijo predstavo o grafih odvisnosti y = x in y = x. Skozi celotno temo avtor predpostavlja aktivno uporabo kalkulatorja, ne le kot orodja za pridobivanje korenov, temveč tudi kot sredstva za ponazoritev nekaterih teoretičnih idej. Zaradi potrebe po uporabi kalkulatorja za pridobivanje kubičnih korenov je uveden drug zapis za koren pozitivnega števila n: a = a 1 n. Članek V. Olkhova opozarja na dejstvo, da je treba pri preučevanju razdelka "Kvadratni koreni" posebno pozornost nameniti transformaciji kompleksnega radikala. Avtor predlaga naslednjo metodologijo, ki daje primer individualne oblike dela z učencem pri študiju teme: Učenec matematičnega razreda je bil pozvan, da z uporabo Vieta izreka najde z izbiro korenine v enačbi x - 7x + 10 = 0, kar je storil brez večjih težav: X 1 = 5, X = (celo malo užaljen zaradi preprostosti vprašanja). Nato je bilo predlagano poenostavitev izraza 7 ± 10. Tukaj bi morali videti polni kvadrat pod radikalom. Ko je predhodno zapisal okorno formulo A ± B= A A B ± A A B, (1) je vanjo nadomestil določene številske vrednosti in dobil ± = 5 ±. Obstaja pa neposredna analogija s prejšnjim primerom 7=5 +, 10=5*, tj. 7 ± 10= 5 + ± 5 = (5 ±) = 5 ± Po tem je učenec samostojno rešil več primerov: 8

29 6 ± 4 = 6 ± 8 = 4 + ± 4 =±, 1 ± 48 = 1 ± 1 = ± 1 1 = 1 ± 1, 18 ± 18 = 18 ± = 16 + ± 16 = 4±, 7 ± 4 = 7 ± 1 = 4 + ± 4 =± in rekel, da zdaj razume, kako je nastala formula (1), čeprav se je ni treba posebej učiti na pamet. A ± B= A ± B 4. Zapiši enačbo: X AX + B = 0, 4 X 1 = A+ A B, X = A A B ; A ± B \u003d A ± B 4 \u003d X 1 + X ± X 1 X \u003d X 1 ± X \u003d A + A B ± A A B, kjer je A> 0, B> 0, A -B> 0 in formula je poenostavljena, ko je A - V natančnem kvadratu. Naloga 1. Pokažite, da je = ; = 1 + Avtor članka V.I. Sedakova ponuja preproste metode, ki vam omogočajo hitro izvajanje dejanj, kot je pridobivanje kvadratnih korenov v mislih. Te metode lahko povečajo produktivnost v razredu, saj ustne in polustne vaje nudijo priložnost za študij velike količine snovi v lekciji, učitelju omogočajo, da oceni pripravljenost razreda 9.

30 k učenju nove snovi. To gradivo je uporabno za bodoče učitelje matematike. Ena glavnih nalog poučevanja matematike v šoli je oblikovanje zavestnih in močnih računalniških spretnosti pri učencih. Računalniške spretnosti so pomemben del matematičnih veščin. Tema ustnega štetja je še posebej pomembna med državnim zaključnim spričevalom (OGE) in enotnim državnim izpitom (USE), kjer uporaba računalniških naprav ni dovoljena. Ustne vaje v kombinaciji z drugimi oblikami dela omogočajo ustvarjanje pogojev, v katerih se aktivirajo različne vrste dejavnosti učencev: mišljenje, govor, motorične sposobnosti. Zato je treba pri vsaki lekciji matematike nameniti do 10 minut za vaje z miselnimi izračuni. Oblikovanje računalniških veščin je kompleksen in sistematičen proces. Sestavljen je iz naslednjih stopenj: Prva stopnja oblikovanja veščine je obvladovanje veščine. Druga stopnja je stopnja avtomatizacije spretnosti. Avtomatizacija veščine je doseči rezultate pri ustnem izvajanju vaj, praktično brez zapiskov, opomb itd. Predstavljajte si sprejem ustnega štetja v temi "Kvadratni koreni" za študente. Izvleček kvadratnega korena večvrednega naravnega števila. Najprej napišemo algoritem za pridobivanje kvadratnega korena v splošni obliki, ki ga lahko uporabimo pri delu z naravnimi števili. 1. Razdelimo število v skupine (od desne proti levi, začenši z zadnjo števko), v vsako skupino vključimo dve sosednji števki. V tem primeru se lahko v zadnji skupini pojavi ena števka (če je število števk liho) in dve števki, če je število števk sodo. Število skupin v takem številu kaže število števk rezultata.

31. Izberemo največje število, tako da njegov kvadrat ne presega števila v zadnji skupini (šteto od desne proti levi); to je prva številka rezultata. Dobili bomo neko število A. S podvojitvijo razpoložljivega dela rezultata dobimo število a. Sedaj izberimo števko x tako, da zmnožek števila a in x ne presega števila A. Števka x je druga števka rezultata. 4. Od števila A odštejemo zmnožek števila a z x, najdeni razliki na desni dodamo tretjo skupino, dobimo neko število B. Podvojimo razpoložljivi del rezultata, dobimo število b. Sedaj izberemo največjo števko y, tako da zmnožek števila z in y ne presega števila B. Števka y je tretja števka rezultata. 5. Naslednji korak pravila ponovi 4. korak. To se nadaljuje, dokler ni uporabljena prva skupina številk. Primer 14. Predstavimo ta algoritem z enostavnejšim primerom, katerega rezultat je očiten. Izračunamo 144. Iz tabele kvadratov naravnih števil znotraj dveh desetic vemo, da je 144 = 1. V številu 144 od desne proti levi ločimo dve števki, 1/44. Dobili smo dve skupini števil, zato je rezultat dvomestno število. Izberemo število, katerega kvadrat ne presega števila v drugi skupini (štejemo od desne proti levi), to je število 1. V našem primeru bo to število število 1, ker njegov kvadrat je enak ena. To pomeni, da bo v odgovoru v kategoriji desetic število 1. Od števila 144 odštejemo dobljeno število desetic, v preostanku dobimo število 44. Določimo število enic v odgovoru. Če želite to narediti, na levi pomnožite dobljeno številko desetin z, dobimo. Izberimo to 1

32 je število, ko ga pomnožimo s samim seboj in z dobljenim številom, dobimo 44. To število je torej, ko izvlečemo kvadratni koren iz 144, dobimo število 1. Izberemo števila odgovora 1_. Odgovor: 144=1. Primer 15. Oglejmo si postopek pridobivanja kvadratnih korenov iz petmestnega števila.Izberemo številke odgovora 4. Odgovor: 54756=4. Zaključki o prvem poglavju V 1. poglavju so bili obravnavani glavni cilji in cilji poučevanja teme "Kvadratni koreni" v tečaju algebre osnovne šole na podlagi Zveznih državnih izobraževalnih standardov LLC in programov matematike. Analiza teoretičnega gradiva in gradiva nalog v učbenikih algebre za 8. razred na to temo je pokazala, da avtorji učbenikov uporabljajo različne pristope k uvajanju samega koncepta kvadratnega korena in k sistemu vaj, ki so osredotočeni na razvijanje veščin izračuna kvadrata korenine in poenostavi številske izraze. Analiza praktičnih izkušenj pri preučevanju teme "Kvadratni koreni" na podlagi člankov in učnih pripomočkov nam omogoča, da sklepamo, da je tema za študente precej težka. Vendar pa lahko s pomočjo ustreznih vaj in posebne tehnike dosežemo solidno asimilacijo pojma kvadratnega korena in njegovih osnovnih lastnosti.

33 POGLAVJE II. METODIČNA PRIPOROČILA ZA ORGANIZACIJO POUKA TEME "KVADRATNI KORENI" V PREDMETU ALGEBRE OSNOVNE ŠOLE 4. Naloge na temo "Kvadratni koreni", osredotočene na osnovno raven znanja in spretnosti pri predmetu algebre osnovne šole šola Vse naloge na temo "Kvadratne korenine", predstavljene v učbenikih algebre 8 razredov, lahko pogojno združimo v 4 skupine: Skupina 1. Naloge za iskanje vrednosti izrazov, ki vsebujejo kvadratne korenine. skupina. Problemi za reševanje kvadratnih enačb z uporabo aritmetičnega kvadratnega korena. skupina. Naloge za poenostavljanje in primerjanje izrazov, ki vsebujejo kvadratne korene. Skupina 4. Naloge za pridobivanje kvadratnega korena. Razmislite o primerih nalog: Skupina 1. Naloge za iskanje vrednosti izrazov, ki vsebujejo kvadratne korene. Primer 1. Poišči vrednost izraza: a) 1,5 0,1 0,5 b) 9 c) 16,. Rešitev: a) Iz definicije aritmetičnega korena sledi, da je 1,5=,5, ker je,5 > 0 in,5 = 1,5; 0,5 = 0,5 ker 0,5 > 0 in 0,5 = 0,5..5 0,1 0,5 = 7 0,05= 6,95 b) 9 = 9, ker 9=9=9

34 c) Ta izraz ni smiseln, ker je kvadrat poljubnega števila nenegativno število. Odgovor: a) 6,95; b) 9; c) izraz nima smisla Primer. Izločite neracionalnost iz imenovalca: 1 a) 4 b) 7 c) Rešitev: 1 a) (1())() 4 1 b) 7 4 (7 4(7)() 7) 4(7 7) 4( 7 4) 7 c) ((5 5 7)(7)(5 5 7) 7) (5 5 7) (5 6) 5 6 Odgovor: a) + b) 7 + c) 5 6 Skupina. Reševanje kvadratnih enačb z uporabo aritmetičnega kvadratnega korena Primer. Poišči vrednost x v izrazu 10x 14 = 11. 4

35 10x 15 x 1,5 Rešitev: 10x x 14 x 15:10 10x x Preveri: , Odgovor: x = 1,5. 4 x x Primer 4. Poišči vrednost x v izrazu 4 x = 1. Rešitev: x 1 Preverjanje: Odgovor: x Skupina. V tej skupini združujemo naloge o poenostavljanju izrazov. 5. primer Poenostavite izraz: 5

36 6 Rešitev: Da se znebite neracionalnosti v imenovalcu ulomka, morate števec in imenovalec tega ulomka pomnožiti z vsoto, če je v imenovalcu razlika, ali števec in imenovalec tega ulomka z razliko, če je imenovalec vsebuje vsoto) () ())(( ))(() ())(())(())(())((Odgovor: 4 6 Primer 6. Poenostavite izraz: 8 4 Rešitev: Odgovor : 6 Primer 7. Poenostavite izraz: ,5 8 Rešitev: ,5 8 (z uporabo izreka o kvadratnem korenu) Odgovor: 5

37 Skupina 4. kvadratni koren. V tej skupini bomo ponudili naloge izločanja Primer 8. Izluščite koren izraza Rešitev: 5a 6 49 Uporabimo izrek o izluščitvi aritmetičnega kvadratnega korena iz ulomka. 5a a a a a 7 6 Uporabimo izrek o pridobivanju aritmetičnega kvadratnega korena iz produkta. 5a a a a 6 Nato uporabimo naslednji izrek: za poljubno število a velja enakost a a a 5a 5a 5 a 5 (a) 5 a 5 a Odgovor: Če je a 0, potem Če je a< 0, то 5 a 7 5 a a 5 7 a Пример 9. Внести множитель под знак корня (буквами обозначены положительные числа): 1) a a 1) x x 5 7

38 1) a Rešitev: a a a a a a (Uporabljen je izrek o recipročnem kvadratnem korenu.) x x x x x x x x (Uporabljen je izrek o recipročnem kvadratnem korenu). Odgovor: 1) a) x 11x 4 1) 64 Primer 10. Izluščite koren: x) 400 a, kjer je a< 0 Решение: 1) 11x x x 4 11 (x 8) 11 x 8 11x 8 1 x 8) 400 a a a a 0 a (Используется теорема об извлечении арифметического квадратного корня из дроби, теорема об извлечении арифметического квадратного корня из произведения и теорема: a a). Ответ: 1) 1 x 8 0 a 8

39 Članek ponuja multivariantna didaktična gradiva (naloge na karticah), ki so namenjena poenostavljanju številskih izrazov s koreni. Učitelju matematike bodo nedvomno v pomoč pri organizaciji samostojnega ali preizkusnega dela. Dajmo možnosti. 1. možnost 1. Poenostavi: Poenostavi: Znebi se neracionalnosti v imenovalcu: Poenostavi izraz Izračunaj: 7 * Poenostavi izraz 6+4 4, Poišči vrednost izraza 8. Izračunaj: * Poišči vrednost izraza 10 Poenostavite izraz ()(75 7) in dokažite, da je dobljeno število koren enačbe x 0 = 0. Možnost 1. Poenostavite:

DELOVNI PROGRAM ZA ALGEBRO ZA 8 RAZRED (splošna izobrazbena raven) Sestavil: Tikhonov VA, učitelj matematike; Obdobje izvajanja programa: 1 leto Program dela temelji na zveznem

MATEMATIKA POJASNILO Ta delovni program je bil razvit na podlagi zvezne sestavine državnega izobraževalnega standarda osnovnega splošnega izobraževanja in programa osnovnega splošnega izobraževanja.

Delovni program za osnovno splošno izobraževanje iz matematike na srednji šoli MBOU 30 Penza (5. razred) Pojasnilo Status dokumenta Delovni program za osnovno splošno izobraževanje iz matematike za 5. razred

Opomba k programu dela pri matematiki v 5. razredu. Pojasnilo Delovni program matematike za šolsko leto 2016-2017 v 5. razredu temelji na: 1. Zvezni zakon 273 FZ 29.12.2012

Pojasnilo Delovni program iz matematike je sestavljen na podlagi naslednjih regulativnih dokumentov in smernic: 1. Zvezni državni izobraževalni standard Basic

Pojasnilo. Ta program dela je namenjen učencem 8. razreda in se izvaja na podlagi naslednjih dokumentov:. Državni standard za osnovno splošno, osnovno splošno in srednješolsko

Delovni kurikulum MATEMATIKA 5-6 razredi študijsko leto 2017-2018 POVZETEK Ta delovni program je bil razvit v skladu z glavnimi določbami Zveznega državnega izobraževalnega

Občinska proračunska izobraževalna ustanova "Srednja šola 17" v Belgorodu "Dogovorjeno" Vodja ShMO N.A. Ilminskaya Protokol 20 "Dogovorjeno" Namestnik direktorja

Delovni program za matematiko za 5. razred

Obravnavano na potrditvenem sestanku Ministrstva za obrambo, direktor učiteljev kulturnih in tehnoloških dejavnosti MKOU LSOSH 1 M. M. Kostin in Odredba službe SPL 109 Protokol 01 z dne 01. septembra 2017. z dne 01. septembra 2017

Priloga k osnovnemu izobraževalnemu programu osnovne splošne izobrazbe ukaz 488os z dne 30.08.208. Tyumenska regija Khanty-Mansiysk avtonomno okrožje Yugra Nizhnevartovsky District

1. Pojasnilo Delovni program v algebri za 9. razred je bil sestavljen na podlagi regulativnih dokumentov ter informacij in metodoloških gradiv: 1. O izobraževanju v Ruski federaciji: zvezna

Koledarsko-tematsko načrtovanje učnega gradiva iz algebre za 8. razred. Pojasnilo Koledarsko-tematsko načrtovanje pri algebri za 8. razred temelji na zglednem programu

Zahteve za stopnjo pripravljenosti dijakov osnovnega splošnega izobraževanja: Dijaki morajo poznati/razumeti: - pomen matematike za reševanje problemov, ki se pojavljajo v teoriji in praksi; zemljepisne širine in ob istem

PROGRAM DELA Razred (stopnja), na kateri se izvaja predmet 8 Predmetno področje Matematika in računalništvo Predmet Matematika (Algebra) Študijsko leto 2017-2018 Število ur na leto 102

Občinska proračunska izobraževalna ustanova Gymnasium 4, Khimki ODOBRENA: Direktor MBOU Gymnasium 4 / N.N. Kozelskaya / Red 2015 Delovni program v algebri (osnovna raven) 8. razred

Obravnavano na seji pedagoškega sveta šole v letu 2009. "Strinjeno" 2009 "Odobrena" direktorica MBOSHI "KSHI" Taipova A.R. 2009

PREGLEDANO: na sestanku MO / ZYMurtazaeva Pr iz SOGLAŠANO: namestnica direktorja za upravljanje vodnih virov / EKKhairetdinova ODOBRENA: Direktor šole / LMAmetova Pr iz DELOVNEGA PROGRAMA Algebra na 8 A MBOU "Starokrymskaya OSH"

Vsebina. Pojasnilo 3 str.

OBČINSKI PRORAČUN SPLOŠNO IZOBRAŽEVALNA INSTITUCIJA SREDNJA IZOBRAŽEVALNA ŠOLA 40 LIPETSK DELOVNI PROGRAM ALGEBRE za učence z motnjami sluha 8. razred

Pojasnilo Ta delovni program predmeta "Algebra" za učence 8. razreda splošne izobraževalne ustanove je bil razvit na podlagi avtorskega programa osnovnega splošnega izobraževanja

Pojasnilo Ta program algebre za glavno splošno šolo 8. razreda je sestavljen na podlagi zvezne komponente državnega standarda za osnovno splošno izobraževanje

1. Načrtovani rezultati obvladovanja predmeta Predmetni rezultati študija predmeta "Matematika" v 6. razredu so oblikovanje naslednjih veščin:

Dodatek k delovnemu programu iz matematike Murmanska regija, okrožje Kola, str. Državna regionalna proračunska izobraževalna ustanova Minkino "Popravni internat Minkino"

Program dela pri matematiki 6. razred. 1. Koledarsko-tematski načrt lekcije Izobraževalni sklopi in teme Datum Število ur I četrtina (42 lekcij) 1. Deljivost števil (20 lekcij) 1.09-28.09 1-3 Delitelji

NAČRTOVANI REZULTATI Osebni metapredmet Predmet začetne predstave o idejah in metodah matematike kot univerzalnega jezika znanosti in tehnologije, sredstva za modeliranje pojavov in procesov;

1 POJASNILO Delovni program za predmet "Algebra" v 9. razredu temelji na zvezni komponenti državnega standarda za osnovno splošno izobraževanje. Ta delovni program

Pojasnilo Delovni program za algebro 8. razred ustreza zvezni komponenti državnega izobraževalnega standarda osnovnega splošnega, osnovnega splošnega in srednjega (popolnega) splošnega

Pojasnilo Delovni program temelji na: - Zvezni sestavini državnega izobrazbenega standarda osnovne splošne izobrazbe matematike - Zglednih programih matematike.

Poglavje UVOD V ALGEBRO .. KVADRAT TRIČLEN ... Babilonski problem iskanja dveh števil z njuno vsoto in produktom. Eden najstarejših problemov v algebri je bil predlagan v Babilonu, kjer

Pojasnilo. Ta delovni program pri predmetu "Matematika" za učence 6. razreda splošne izobraževalne ustanove je bil razvit na podlagi avtorskega programa S.M. Nikolski, M. K. Potapov,

POJASNILO. (Matematika 5. razred) Ta delovni program je sestavljen v skladu z državnim programom matematike za splošne izobraževalne ustanove Ministrstva za šolstvo Ruske federacije.

Pojasnilo Delovni program v algebri je bil razvit na podlagi naslednjih regulativnih pravnih dokumentov: Zvezni zakon št. 273-FZ z dne 29. decembra 2012 "O izobraževanju v Ruski federaciji"; naročilo

Pojasnilo Delovni program algebre za 8. razred je bil sestavljen v skladu z določbami Zveznega državnega izobraževalnega standarda za osnovno splošno izobraževanje druge generacije,

Status dokumenta Pojasnilo

Upoštevano Sprejeto Odobreno Na MO učiteljev matematike na seji Direktor MOU SOSH Protokol 1 z dne 26.08. 2014. pedagoški str. Poima Vodja MO Praslova O.M. Svet Rodionova O.I. Protokol 1

Zasebna izobraževalna ustanova Lyceum 1 "Sputnik" PREDSTAVLJENO Na seji Metodološkega sveta Lyceum 1 "Sputnik" Zapisnik 2017 Predsednik metodološkega sveta liceja 1 "Sputnik" Ursul

Opomba k delovnemu programu 8. razred, algebra

1. Pojasnilo. Delovni program pri algebri je sestavljen na podlagi avtorskega programa "Algebra 8kl." izd. Makarychev in drugi v skladu z vsebino vsebine izobraževalnih predmetov komponente države

DELOVNI PROGRAM PRI ALGEBRI IN GEOMETRIJI ZA 7. "A" RAZRED ZA ŠTUDIJSKO LETO 2018 2019

Občinski proračunski izobraževalni zavod Srednja šola 4 Obravnavano na pedagoškem svetu Zapisnik 1 z dne 31.08. 2017 Odredba 162 z dne 31.08.2017 ODOBRENA: Direktor

Kontrolni in merilni materiali za vmesno certificiranje iz matematike v letu 2018 7. razred Pojasnilo Vsebina dela je zgrajena v skladu z: z zveznim zakonom Ruske federacije

Pojasnilo Regulativni dokumenti Program dela temelji na: zveznem zakonu Ruske federacije z dne 9..0 leta 73-FZ "O izobraževanju v Ruski federaciji" zvezne komponente

Pojasnilo Delovni program temelji na: Odredbi Ministrstva za izobraževanje Ruske federacije z dne 05.03.2004 1089 "O odobritvi zvezne komponente državnih izobraževalnih standardov

1. NAČRTOVANI IZIDI OSVAJANJA PREDMETA Uk matematike v osnovni šoli omogoča učencem doseganje naslednjih rezultatov: V smeri osebnega razvoja: - sposobnost jasnega,

POJASNILO Delovni program algebre za 8. razred je bil sestavljen v skladu z določbami Zveznega državnega izobraževalnega standarda za osnovno splošno izobraževanje druge generacije,

DODATEK k izobraževalnemu programu KOLEDAR TEMATSKO NAČRTOVANJE algebre v 8. razredu Učbenik "ALGEBRA 8", avtor Yu. N. Makarychev in drugi, uredil S. A. Telyakovsky Učitelj: Dudnikova

Pojasnilo Program algebre za osnovno šolo je sestavljen v skladu z zahtevami: - zvezne komponente državnega izobraževalnega standarda za osnovno splošno izobraževanje

Pojasnilo Delovni program algebre za 8. razred (poglobljeni študij) je bil sestavljen v skladu z zvezno komponento državnega izobraževalnega standarda, program algebra

MINISTRSTVO ZA IZOBRAŽEVANJE IN ZNANOST RUSKE FEDERACIJE NOVOSIBIRSK DRŽAVNA UNIVERZITETNI SPECIALIZIRANI IZOBRAŽEVALNI IN ZNANSTVENI CENTER Matematika 8. razred Polinomi Novosibirsk Polinomi Rational

Program dela je sestavljen v skladu z naslednjimi regulativnimi dokumenti: Zvezni zakon št. 273-FZ z dne 29. februarja 202 "O izobraževanju v Ruski federaciji", zahteve Zveznega državnega izobraževalnega

Pojasnilo Ta delovni program "Algebra" je bil razvit na podlagi: - Zveznega zakona z dne 29. decembra 2012 273-FZ (s spremembami 13. julija 2015) "O izobraževanju v Ruski federaciji"; - na podlagi avtorskih pravic

Program dela je bil sestavljen v skladu z regulativnimi dokumenti: Zvezni zakon št. 273-FZ z dne 29. februarja 202 "O izobraževanju v Ruski federaciji". 2. Odredba Ministrstva za izobraževanje in znanost Ruske federacije

Ministrstvo za splošno in poklicno izobraževanje RO

državna proračunska izobraževalna ustanova

osnovno poklicno izobraževanje v regiji Rostov

strokovna šola št.5

Praktično delo

v disciplini ODP. 01."Matematika: Algebra in začetki

matematična analiza; geometrija"

na to temo: "Pretvorbe izrazov, ki vsebujejo korene, potence in logaritme».

Zaštudenti jaz seveda

G. Rostov na Donu

2017

Oddelek številka 1. Algebra.

Tema 1.2. Koreni, potence in logaritmi.

Praktična lekcija številka 1.

Zadeva: "Pretvorbe izrazov, ki vsebujejo korene, potence in logaritme".

Cilj: vedeti lastnosti radikalov, potence in logaritmov; jih znati uporabiti izvajanje transformacij izrazov, ki vsebujejo korene, stopnje in logaritme.

Število ur : 1 uro.

teoretično gradivo.

Korenine.

Dejanje, s katerim najdemo korenn-te stopnje, se imenuje izvlečenje koreninn- stopnja.

Opredelitev. Aritmetični koren naravne stopnjen≥ 2 iz nenegativnega števila a imenujemo nenegativno število,nkaterega potenca je a.

Aritmetični koren druge stopnje imenujemo tudi kvadratni koren, koren tretje stopnje pa tudi kubni koren.

Na primer.

Izračunajte:

aritmetični korennstopnje ima naslednje lastnosti:

če je a ≥ 0, b > 0 in n, mso naravna števila inn ≥ 2, m≥ 2, torej

1. 3.

2. 4.

Primeri uporabe lastnosti aritmetičnega korena.

Lastnosti stopnje z racionalnim eksponentom.

Za poljubna racionalna števila p in k ter poljubna a > 0 in b > 0 veljajo enakosti:

1. ; 2. ;

3. ; 4. ;

5. .

Primeri uporabe lastnosti stopnje:

1). 7*

4). .

Logaritem števila

Opredelitev. Logaritem pozitivnega številabv osnovi a, kjera > 0, a≠ 1, imenovan eksponent, na katerega je treba število povečatia, Za pridobitev b.

a = b je osnovna logaritemska identiteta.

Lastnosti logaritmov

Pustiti a > 0, a ≠ 1, b>0, c >0, k je poljubno realno število. Potem veljajo formule:

1 . dnevnik ( pr ) = logb + logc , 4. logb = ,

2. log = log - log c, 5.dnevnik a = 1 ,

3. dnevnik b = do * logb , 6. dnevnik 0 = 1 .

Primeri uporabe formul:

log2 + log 18 =log( 2 * 18 ) = dnevnik 36 = 2;

dnevnik 48 -log 4 = dnevnik= dnevnik 12 = 1;

dnevnik 9 = * dnevnik 9 = .

Odločite se sami .

Naloge.

1 možnost

1. Izračunaj:

1) ; 4) dnevnik ;

2) ; 5) 0,5;

3) ; 6) 3 dnevnik 2 - dnevnik 64.

2, če je x = 7.

3. Primerjaj številke:dnevnik 11 in dnevnik 19.

4. Poenostavi: 1) ; 2).

5. Izračunaj: dnevnikdnevnikdnevnik 3.

_________________________________________________________________

Možnost 2

1. Izračunaj:

1) ; 4) dnevnik 64;

2) ; 5) ;

3) ; 6) 2 dnevnik 3 - dnevnik 81.

2. Poiščite vrednost izraza: 3, če je y = 2.

3. Primerjaj številke:dnevnik in dnevnik.

4. Poenostavi: 1) ; 2).

5. Izračunaj: dnevnikdnevnikdnevnik 2.

__________________________________________________________________

Merila za ocenjevanje:

11 pravilnih nalog - "5";

9 - 10 pravilnih nalog - "4";

7 - 8 pravilnih nalog - "3".

Bašmakov. M. I. Matematika: učbenik za NVO in SPO. - M.:

Založniški center "Akademija", 2013.

Alimov Sh.A. et al. Algebra in začetki analize. 10 (11) razred. – M.: 2012.

Algebra. 9. razred: učbenik, naloga za splošno izobraževanje. ustanove/

A.G. Mordkovich in drugi - M .: Mnemozina, 2009.

Algebra. 8. razred: učbenik, naloga za splošno izobraževanje. ustanove/

A.G. Mordkovich in drugi - M .: Mnemozina, 2008.

Algebra. 7. razred: učbenik, naloga za splošno izobraževanje. ustanove/

A.G. Mordkovich in drugi - M .: Mnemozina, 2007.

Obrazec za poročanje: preverjanje nalog s strani učitelja

Za uspešno uporabo operacije pridobivanja korena v praksi se morate seznaniti z lastnostmi te operacije.
Vse lastnosti so oblikovane in dokazane samo za nenegativne vrednosti spremenljivk, ki jih vsebujejo korenski znaki.

1. izrek. N-ti koren (n=2, 3, 4,...) produkta dveh nenegativnih naborov čipov je enak produktu n-tih korenin teh števil:

komentar:

1. Izrek 1 ostaja veljaven za primer, ko je radikalni izraz produkt več kot dveh nenegativnih števil.

2. izrek.če, in je n naravno število, večje od 1, potem je enakost

Na kratko(čeprav netočna) formulacija, ki je primernejša za uporabo v praksi: koren ulomka je enak ulomku korenov.

Izrek 1 nam omogoča množenje m samo korenine iste stopnje , tj. samo koreni z istim eksponentom.

Izrek 3. Če ,k je naravno število in n je naravno število, večje od 1, potem velja enakost

Z drugimi besedami, da dvignete koren na naravno moč, je dovolj, da dvignete korenski izraz na to moč.
To je posledica izreka 1. Dejansko, na primer, za k = 3 dobimo

Izrek 4. Če ,k, n naravna števila, večja od 1, potem velja enakost

Z drugimi besedami, da izvlečemo koren iz korena, je dovolj, da pomnožimo eksponente korenin.
na primer

Bodi previden! Naučili smo se, da lahko nad koreni izvajamo štiri operacije: množenje, deljenje, potenciranje in izločanje korena (iz korena). Kaj pa seštevanje in odštevanje korenov? Ni šans.
Na primer, ne morete pisati namesto Indeed, vendar je to očitno

Izrek 5. Če indikatorja korena in korenskega izraza pomnožimo ali delimo z istim naravnim številom, potem se vrednost korena ne spremeni, tj.

Primeri reševanja problemov

Primer 1 Izračunaj

rešitev. Z uporabo prve lastnosti korenin (izrek 1) dobimo:

Primer 2 Izračunaj
rešitev. Pretvorite mešano število v nepravilni ulomek.
Imamo uporabo druge lastnosti korenin ( izrek 2 ), dobimo:

Primer 3 Izračunajte:

rešitev. Vsaka formula v algebri, kot dobro veste, se uporablja ne samo "od leve proti desni", ampak tudi "od desne proti levi". Torej, prva lastnost korenin pomeni, da jo je mogoče predstaviti kot in, nasprotno, nadomestiti z izrazom. Enako velja za drugo lastnost korenin. S tem v mislih naredimo izračune.

Čestitamo: danes bomo analizirali korenine - eno najbolj osupljivih tem 8. razreda. :)

Marsikdo se zmede glede korenin ne zato, ker so zapletene (kar je zapleteno - par definicij in še par lastnosti), temveč zato, ker so v večini šolskih učbenikov korenine definirane skozi takšne divjine, da jih lahko le avtorji učbenikov sami. razumej to čečkanje. Pa še to samo s steklenico dobrega viskija. :)

Zato bom zdaj dal najbolj pravilno in najbolj kompetentno definicijo korena - edino, ki si jo resnično morate zapomniti. In šele nato bom pojasnil: zakaj je vse to potrebno in kako to uporabiti v praksi.

Najprej pa si zapomnite eno pomembno točko, na katero iz nekega razloga mnogi sestavljalci učbenikov "pozabijo":

Koreni so lahko sode stopnje (naš najljubši $\sqrt(a)$, pa tudi poljubni $\sqrt(a)$ in sodi $\sqrt(a)$) in lihe stopnje (poljubni $\sqrt(a)$ , $\ sqrt(a)$ itd.). In definicija korena lihe stopnje je nekoliko drugačna od sode.

Tukaj v tem prekletem "nekoliko drugačnem" se skriva verjetno 95% vseh napak in nesporazumov, povezanih s koreninami. Zato enkrat za vselej razčistimo terminologijo:

Opredelitev. Celo koren n iz števila $a$ je katerikoli nenegativnoštevilo $b$ tako, da je $((b)^(n))=a$. In koren lihe stopnje iz istega števila $a$ je na splošno poljubno število $b$, za katerega velja enaka enakost: $((b)^(n))=a$.

V vsakem primeru je koren označen takole:

\(a)\]

Število $n$ v takem zapisu imenujemo korenski eksponent, število $a$ pa radikalni izraz. Zlasti za $n=2$ dobimo naš "najljubši" kvadratni koren (mimogrede, to je koren sode stopnje), za $n=3$ pa dobimo kubični koren (liho stopnjo), kar pogosto najdemo tudi v problemih in enačbah.

Primeri. Klasični primeri kvadratnih korenov:

\[\begin(align) & \sqrt(4)=2; \\ & \sqrt(81)=9; \\ & \sqrt(256)=16. \\ \end(align)\]

Mimogrede, $\sqrt(0)=0$ in $\sqrt(1)=1$. To je povsem logično, saj $((0)^(2))=0$ in $((1)^(2))=1$.

Pogoste so tudi kubične korenine - ne bojte se jih:

\[\begin(align) & \sqrt(27)=3; \\ & \sqrt(-64)=-4; \\ & \sqrt(343)=7. \\ \end(align)\]

No, nekaj "eksotičnih primerov":

\[\begin(align) & \sqrt(81)=3; \\ & \sqrt(-32)=-2. \\ \end(align)\]

Če ne razumete, kakšna je razlika med sodo in liho stopnjo, še enkrat preberite definicijo. Zelo pomembno je!

Medtem pa bomo razmislili o eni neprijetni lastnosti korenov, zaradi katere smo morali uvesti ločeno definicijo za sode in lihe eksponente.

Zakaj sploh potrebujemo korenine?

Po branju definicije se bo marsikateri študent vprašal: "Kaj so matematiki pokadili, ko so se tega domislili?" In res: zakaj potrebujemo vse te korenine?

Za odgovor na to vprašanje se za trenutek vrnimo v osnovno šolo. Ne pozabite: v tistih daljnih časih, ko so bila drevesa bolj zelena in so bili cmoki okusnejši, je bila naša glavna skrb pravilno pomnožiti števila. No, nekaj v duhu "pet po pet - petindvajset", to je vse. Toda navsezadnje lahko številke pomnožite ne v parih, ampak v trojčkih, štirih in na splošno celih nizih:

\[\begin(align) & 5\cdot 5=25; \\ & 5\cdot 5\cdot 5=125; \\ & 5\cdot 5\cdot 5\cdot 5=625; \\ & 5\cdot 5\cdot 5\cdot 5\cdot 5=3125; \\ & 5\cdot 5\cdot 5\cdot 5\cdot 5\cdot 5=15\ 625. \end(align)\]

Vendar to ni bistvo. Trik je drugačen: matematiki so leni ljudje, zato so morali množenje desetih petic zapisati takole:

Tako so prišli do diplom. Zakaj ne bi zapisali števila faktorjev kot nadnapis namesto dolgega niza? kot ta:

Zelo je priročno! Vsi izračuni so večkrat zmanjšani in ne morete porabiti kupa pergamentnih listov zvezkov, da bi zapisali nekaj 5 183 . Tak zapis so poimenovali stopnja števila, v njem so našli kup lastnosti, a sreča se je izkazala za kratkotrajno.

Po veličastnem pijančevanju, ki je bilo organizirano ravno o »odkritju« stopinj, se je neki še posebej okajeni matematik nenadoma vprašal: »Kaj pa, če poznamo stopnjo števila, ne poznamo pa števila samega?« Dejansko, če vemo, da določeno število $b$ na primer daje 243 na 5. potenco, kako potem lahko uganemo, čemu je enako število samo $b$?

Ta problem se je izkazal za veliko bolj globalnega, kot se morda zdi na prvi pogled. Ker se je izkazalo, da za večino "gotovih" diplom ni takih "začetnih" številk. Presodite sami:

\[\begin(align) & ((b)^(3))=27\Rightarrow b=3\cdot 3\cdot 3\Rightarrow b=3; \\ & ((b)^(3))=64\Desna puščica b=4\cdot 4\cdot 4\Desna puščica b=4. \\ \end(align)\]

Kaj pa, če $((b)^(3))=50$? Izkazalo se je, da morate najti določeno število, ki nam bo, če ga trikrat pomnožimo, dalo 50. Toda kaj je to število? Očitno je večje od 3, ker je 3 3 = 27< 50. С тем же успехом оно меньше 4, поскольку 4 3 = 64 >50. tj. to število leži nekje med tri in štiri, čemu pa je enako - FIG boste razumeli.

Prav zato so matematiki prišli do $n$-tih korenin. Zato je bila uvedena radikalna ikona $\sqrt(*)$. Za označevanje istega števila $b$, ki nam bo na določeno potenco dalo predhodno znano vrednost

\[\sqrt[n](a)=b\Desna puščica ((b)^(n))=a\]

Ne trdim: pogosto se te korenine zlahka upoštevajo - zgoraj smo videli več takih primerov. A vseeno, če si v večini primerov zamislite poljubno število in nato iz njega poskušate izluščiti koren poljubne stopnje, vas čaka huda nesreča.

Kaj je tam! Tudi najpreprostejšega in najbolj poznanega $\sqrt(2)$ ni mogoče predstaviti v naši običajni obliki - kot celo število ali ulomek. In če to številko vnesete v kalkulator, boste videli tole:

\[\sqrt(2)=1,414213562...\]

Kot lahko vidite, je za decimalno vejico neskončno zaporedje števil, ki ne sledijo nobeni logiki. To številko lahko seveda zaokrožite, da jo hitro primerjate z drugimi številkami. Na primer:

\[\sqrt(2)=1,4142...\približno 1,4 \lt 1,5\]

Ali tukaj je še en primer:

\[\sqrt(3)=1,73205...\približno 1,7 \gt 1,5\]

Toda vse te zaokrožitve so, prvič, precej grobe; in drugič, znati morate delati tudi s približnimi vrednostmi, sicer lahko ujamete kup neočitnih napak (mimogrede, spretnost primerjave in zaokroževanja se nujno preverja na profilnem izpitu).

Zato v resni matematiki brez korenin ne gre - so enaki enakovredni predstavniki množice vseh realnih števil $\mathbb(R)$, kot so ulomki in cela števila, ki jih že dolgo poznamo.

Nezmožnost predstavitve korena kot ulomka oblike $\frac(p)(q)$ pomeni, da ta koren ni racionalno število. Takšna števila se imenujejo iracionalna in jih ni mogoče natančno predstaviti, razen s pomočjo radikala ali drugih konstrukcij, posebej zasnovanih za to (logaritmi, stopinje, meje itd.). A o tem kdaj drugič.

Razmislite o nekaj primerih, kjer bodo po vseh izračunih v odgovoru še vedno ostala iracionalna števila.

\[\begin(align) & \sqrt(2+\sqrt(27))=\sqrt(2+3)=\sqrt(5)\približno 2.236 ... \\ & \sqrt(\sqrt(-32 ))=\sqrt(-2)\približno -1,2599... \\ \end(align)\]

Seveda je po videzu korena skoraj nemogoče uganiti, katera števila bodo prišla za decimalno vejico. Je pa možno računati na kalkulatorju, vendar nam tudi najnaprednejši datumski kalkulator poda le prvih nekaj števk iracionalnega števila. Zato je veliko pravilneje odgovore zapisati kot $\sqrt(5)$ in $\sqrt(-2)$.

Za to so bili izumljeni. Za lažje zapisovanje odgovorov.

Zakaj sta potrebni dve definiciji?

Pozorni bralec je verjetno že opazil, da so vsi kvadratni koreni, navedeni v primerih, vzeti iz pozitivnih števil. No, vsaj od nule. Toda kockaste korenine se mirno izvlečejo iz absolutno katerega koli števila - tudi pozitivnega, tudi negativnega.

Zakaj se to dogaja? Oglejte si graf funkcije $y=((x)^(2))$:

Graf kvadratne funkcije daje dva korena: pozitivno in negativno

Poskusimo izračunati $\sqrt(4)$ z uporabo tega grafa. Da bi to naredili, je na grafu narisana vodoravna črta $y=4$ (označena z rdečo), ki seka parabolo v dveh točkah: $((x)_(1))=2$ in $((x) _(2)) =-2$. To je povsem logično, saj

S prvo številko je vse jasno - pozitivna je, zato je koren:

Toda kaj potem storiti z drugo točko? Ali ima 4 dva korena hkrati? Konec koncev, če kvadriramo število −2, dobimo tudi 4. Zakaj potem ne bi zapisali $\sqrt(4)=-2$? In zakaj učitelji gledajo takšne zapise, kot da te hočejo pojesti? :)

Težava je v tem, da če ne bodo postavljeni nobeni dodatni pogoji, bodo štiri imele dva kvadratna korena - pozitivno in negativno. In vsako pozitivno število jih bo imelo tudi dva. Toda negativna števila sploh ne bodo imela korenin - to je razvidno iz istega grafa, saj parabola nikoli ne pade pod os l, tj. ne zavzema negativnih vrednosti.

Podoben problem se pojavi pri vseh korenih s sodim eksponentom:

1. Strogo gledano bo imelo vsako pozitivno število dva korena s sodim eksponentom $n$;
2. Iz negativnih števil se koren s parimi $n$ sploh ne izlušči.

Zato definicija sodega korena $n$ posebej določa, da mora biti odgovor nenegativno število. Tako se znebimo dvoumnosti.

Toda za lihih $n$ te težave ni. Da bi to videli, si oglejmo graf funkcije $y=((x)^(3))$:

Kubična parabola zavzame poljubno vrednost, zato lahko kubični koren vzamemo iz poljubnega števila

Iz tega grafa lahko potegnemo dva zaključka:

1. Veje kubične parabole, za razliko od običajne, gredo v neskončnost v obe smeri - tako navzgor kot navzdol. Torej, na kateri koli višini narišemo vodoravno črto, se bo ta črta zagotovo sekala z našim grafom. Zato lahko kockasti koren vedno vzamemo iz popolnoma katerega koli števila;
2. Poleg tega bo takšno križišče vedno edinstveno, zato vam ni treba razmišljati o tem, katero številko je treba šteti za "pravilen" koren in katero točkovati. Zato je definicija korenov za liho stopnjo enostavnejša kot za sodo (ni zahteve po nenegativnosti).

Škoda, da te preproste stvari v večini učbenikov niso razložene. Namesto tega se naši možgani začnejo dvigovati z vsemi vrstami aritmetičnih korenov in njihovih lastnosti.

Da, ne trdim: kaj je aritmetična korenina - tudi morate vedeti. In o tem bom podrobno govoril v ločeni lekciji. Danes bomo o tem tudi govorili, saj bi brez tega vsi razmisleki o koreninah $n$-te množice bili nepopolni.

Toda najprej morate jasno razumeti definicijo, ki sem jo dal zgoraj. V nasprotnem primeru se bo zaradi obilice izrazov v vaši glavi začela taka zmešnjava, da na koncu ne boste razumeli čisto nič.

In vse, kar morate razumeti, je razlika med sodimi in lihimi števili. Zato bomo še enkrat zbrali vse, kar resnično morate vedeti o koreninah:

1. Sodi koren obstaja le iz nenegativnega števila in je sam vedno nenegativno število. Za negativna števila je tak koren nedefiniran.
2. Toda koren lihe stopnje obstaja iz katerega koli števila in je sam lahko poljubno število: za pozitivna števila je pozitiven, za negativna števila pa, kot namiguje kapica, negativen.

Je težko? Ne, ni težko. To je jasno? Ja, očitno je! Zato bomo zdaj malo vadili z izračuni.

Osnovne lastnosti in omejitve

Korenine imajo veliko čudnih lastnosti in omejitev - to bo ločena lekcija. Zato bomo zdaj upoštevali le najpomembnejši "čip", ki velja samo za korenine s celo eksponentom. To lastnost zapišemo v obliki formule:

\[\sqrt(((x)^(2n)))=\levo| x\desno|\]

Z drugimi besedami, če število dvignemo na sodo potenco in nato iz tega izvlečemo koren iste stopnje, ne bomo dobili prvotnega števila, temveč njegov modul. To je preprost izrek, ki ga je enostavno dokazati (zadostuje, da ločeno obravnavamo nenegativne $x$ in nato ločeno obravnavamo negativne). Učitelji nenehno govorijo o tem, podano je v vsakem šolskem učbeniku. Čim pa gre za reševanje iracionalnih enačb (tj. enačb s predznakom radikala), učenci skupaj pozabijo na to formulo.

Da bi podrobno razumeli težavo, za minuto pozabimo na vse formule in poskusimo prešteti dve številki naprej:

\[\sqrt(((3)^(4)))=?\quad \sqrt(((\levo(-3 \desno))^(4)))=?\]

To so zelo preprosti primeri. Prvi primer bo rešila večina ljudi, pri drugem pa se mnogi držijo. Če želite takšno sranje rešiti brez težav, vedno upoštevajte postopek:

1. Najprej se število dvigne na četrto potenco. No, nekako je enostavno. Dobili bomo novo številko, ki jo najdemo celo v tabeli množenja;
2. In zdaj je treba iz te nove številke izluščiti koren četrte stopnje. Tisti. ni "zmanjševanja" korenin in stopinj - to so zaporedna dejanja.

Ukvarjajmo se s prvim izrazom: $\sqrt(((3)^(4)))$. Očitno morate najprej izračunati izraz pod korenom:

\[((3)^(4))=3\cdot 3\cdot 3\cdot 3=81\]

Nato izvlečemo četrti koren števila 81:

Sedaj pa naredimo isto z drugim izrazom. Najprej dvignemo število −3 na četrto potenco, za kar ga moramo 4-krat pomnožiti s samim seboj:

\[((\levo(-3 \desno))^(4))=\levo(-3 \desno)\cdot \levo(-3 \desno)\cdot \levo(-3 \desno)\cdot \ levo(-3 \desno)=81\]

Dobili smo pozitivno število, saj je skupno število minusov v izdelku 4 kosi in vsi se bodo izničili (navsezadnje minus za minus daje plus). Nato znova izvlecite koren:

Te vrstice načeloma ne bi bilo mogoče napisati, saj ni pametno, da bo odgovor enak. Tisti. sodi koren iste sode moči "sežge" minuse in v tem smislu se rezultat ne razlikuje od običajnega modula:

\[\begin(align) & \sqrt(((3)^(4)))=\left| 3\desno|=3; \\ & \sqrt(((\levo(-3 \desno))^(4)))=\levo| -3 \desno|=3. \\ \end(align)\]

Ti izračuni se dobro ujemajo z definicijo korena sode stopnje: rezultat je vedno nenegativen in predznak radikala je prav tako vedno nenegativno število. V nasprotnem primeru koren ni definiran.

Opomba o vrstnem redu operacij

1. Zapis $\sqrt(((a)^(2)))$ pomeni, da najprej kvadriramo število $a$, nato pa dobimo kvadratni koren. Zato smo lahko prepričani, da je nenegativno število vedno pod znakom korena, saj je $((a)^(2))\ge tako ali tako 0$;
2. Zapis $((\left(\sqrt(a) \right))^(2))$ pa nasprotno pomeni, da iz nekega števila $a$ najprej izluščimo koren in šele nato rezultat kvadriramo. Zato število $a$ v nobenem primeru ne more biti negativno - to je obvezna zahteva, vgrajena v definicijo.

V nobenem primeru torej ne bi smeli nepremišljeno zmanjševati korenov in stopenj, s čimer naj bi "poenostavili" prvotni izraz. Ker če je pod korenom negativno število in je njegov eksponent sodo, bomo imeli veliko težav.

Vendar pa so vse te težave pomembne samo za sode kazalnike.

Odstranitev znaka minus izpod znaka korena

Seveda imajo koreni z lihimi eksponenti tudi svojo lastnost, ki je za sode načeloma ni. namreč:

\[\sqrt(-a)=-\sqrt(a)\]

Skratka, minus lahko vzamete izpod znaka korenin lihe stopnje. To je zelo uporabna lastnost, ki vam omogoča, da "vržete" vse minuse:

\[\begin(align) & \sqrt(-8)=-\sqrt(8)=-2; \\ & \sqrt(-27)\cdot \sqrt(-32)=-\sqrt(27)\cdot \left(-\sqrt(32) \desno)= \\ & =\sqrt(27)\cdot \sqrt(32)= \\ & =3\cdot 2=6. \end(align)\]

Ta preprosta lastnost močno poenostavi številne izračune. Zdaj vam ni treba skrbeti: kaj, če je negativni izraz prišel pod koren in se je stopnja v korenu izkazala za enakomerno? Dovolj je, da vse minuse "vržemo ven" zunaj korenin, nato pa jih lahko med seboj pomnožimo, razdelimo in na splošno naredimo veliko sumljivih stvari, ki nas v primeru "klasičnih" korenin zagotovo pripeljejo do napake .

In tu na sceno stopi druga definicija - prav tista, s katero večina šol začne študij iracionalnih izrazov. In brez katerega bi bilo naše sklepanje nepopolno. Srečati!

aritmetični koren

Za trenutek predpostavimo, da so pod korenom lahko samo pozitivna števila ali v skrajnem primeru nič. Ocenjujmo za sode/lihe kazalnike, ocenjujemo za vse zgoraj navedene definicije - delali bomo samo z nenegativnimi števili. Kaj potem?

In potem dobimo aritmetični koren - delno seka z našimi "standardnimi" definicijami, vendar se od njih še vedno razlikuje.

Opredelitev. Aritmetični koren $n$te stopnje nenegativnega števila $a$ je nenegativno število $b$, tako da je $((b)^(n))=a$.

Kot lahko vidite, nas pariteta ne zanima več. Namesto tega se je pojavila nova omejitev: radikalni izraz je zdaj vedno nenegativen in sam koren je prav tako nenegativen.

Da bi bolje razumeli, kako se aritmetični koren razlikuje od običajnega, si oglejte grafe kvadratne in kubične parabole, ki so nam že znane:

Območje iskanja korena - nenegativna števila

Kot lahko vidite, nas od zdaj naprej zanimajo samo tisti deli grafov, ki se nahajajo v prvi koordinatni četrtini - kjer sta koordinati $x$ in $y$ pozitivni (ali vsaj nič). Ni vam več treba pogledati indikatorja, da bi razumeli, ali imamo pravico koreniti negativno število ali ne. Ker se negativna števila načeloma ne upoštevajo več.

Morda se boste vprašali: "No, zakaj potrebujemo tako kastrirano definicijo?" Ali: "Zakaj se ne moremo sprijazniti z zgoraj navedeno standardno definicijo?"

No, dal bom samo eno lastnost, zaradi katere nova definicija postane ustrezna. Na primer, pravilo potenciranja:

\[\sqrt[n](a)=\sqrt(((a)^(k)))\]

Upoštevajte: radikalni izraz lahko dvignemo na poljubno potenco in hkrati pomnožimo korenski eksponent z isto potenco - in rezultat bo isto število! Tukaj je nekaj primerov:

\[\begin(align) & \sqrt(5)=\sqrt(((5)^(2)))=\sqrt(25) \\ & \sqrt(2)=\sqrt(((2)^ (4)))=\sqrt(16) \\ \end(align)\]

No, kaj je narobe s tem? Zakaj tega nismo mogli narediti prej? Evo zakaj. Razmislite o preprostem izrazu: $\sqrt(-2)$ je število, ki je povsem običajno v našem klasičnem smislu, vendar popolnoma nesprejemljivo z vidika aritmetičnega korena. Poskusimo ga pretvoriti:

$\begin(align) & \sqrt(-2)=-\sqrt(2)=-\sqrt(((2)^(2)))=-\sqrt(4) \lt 0; \\ & \sqrt(-2)=\sqrt(((\left(-2 \desno))^(2)))=\sqrt(4) \gt 0. \\ \end(align)$

Kot lahko vidite, smo v prvem primeru minus vzeli izpod radikala (imamo vso pravico, saj je indikator liho), v drugem pa smo uporabili zgornjo formulo. Tisti. z vidika matematike je vse narejeno po pravilih.

WTF?! Kako je lahko isto število hkrati pozitivno in negativno? Ni šans. Samo formula za potenciranje, ki odlično deluje pri pozitivnih številih in ničli, začne v primeru negativnih števil dajati popolno herezijo.

Tukaj, da bi se znebili takšne dvoumnosti, so prišli do aritmetičnih korenin. Posvečena jim je posebna velika lekcija, kjer podrobno obravnavamo vse njihove lastnosti. Zato se zdaj ne bomo zadrževali na njih - lekcija se je vseeno izkazala za predolgo.

Algebrski koren: za tiste, ki želijo vedeti več

Dolgo sem razmišljal: narediti to temo v ločenem odstavku ali ne. Na koncu sem se odločil, da grem od tu. To gradivo je namenjeno tistim, ki želijo še bolje razumeti korenine - ne več na povprečni "šolski" ravni, ampak na ravni blizu olimpijade.

Torej: poleg "klasične" definicije korena $n$-te stopnje iz števila in s tem povezane delitve na sode in lihe indikatorje, obstaja bolj "odrasla" definicija, ki ni odvisna od paritete in sploh druge tankosti. To se imenuje algebraični koren.

Opredelitev. Algebraični $n$-ti koren poljubnega $a$ je množica vseh števil $b$, tako da je $((b)^(n))=a$. Za takšne korenine ni uveljavljenega poimenovanja, zato na vrh postavite pomišljaj:

\[\overline(\sqrt[n](a))=\levo\( b\levo| b\in \mathbb(R);((b)^(n))=a \desno. \desno\) \]

Bistvena razlika od standardne definicije, podane na začetku lekcije, je v tem, da algebraični koren ni določeno število, ampak niz. In ker delamo z realnimi števili, je ta niz samo treh vrst:

1. Prazen komplet. Pojavi se, ko je treba najti algebraični koren sode stopnje iz negativnega števila;
2. Komplet, sestavljen iz enega samega elementa. Vse korenine lihih potenc, kot tudi korenine sodih potenc iz nič, spadajo v to kategorijo;
3. Končno lahko nabor vključuje dve števili - isto $((x)_(1))$ in $((x)_(2))=-((x)_(1))$, ki smo ju videli na grafikon kvadratne funkcije. V skladu s tem je takšna poravnava možna le pri izločanju korena sode stopnje iz pozitivnega števila.

Zadnji primer si zasluži podrobnejšo obravnavo. Preštejmo nekaj primerov, da bomo razumeli razliko.

Primer. Izračunaj izraze:

\[\overline(\sqrt(4));\quad \overline(\sqrt(-27));\quad \overline(\sqrt(-16)).\]

rešitev. Prvi izraz je preprost:

\[\overline(\sqrt(4))=\levo\( 2;-2 \desno\)\]

To sta dve številki, ki sta del niza. Ker vsak od njih na kvadrat daje štirico.

\[\overline(\sqrt(-27))=\levo\( -3 \desno\)\]

Tukaj vidimo niz, sestavljen iz samo ene številke. To je povsem logično, saj je eksponent korena lih.

Na koncu še zadnji izraz:

\[\overline(\sqrt(-16))=\varnič \]

Dobili smo prazen komplet. Ker ni niti enega realnega števila, ki bi nam, če bi ga dvignili na četrto (torej sodo!) potenco, dalo negativno število −16.

Končna opomba. Pozor: nisem slučajno povsod zapisal, da delamo z realnimi številkami. Ker obstajajo tudi kompleksna števila - tam je povsem mogoče izračunati $\sqrt(-16)$ in še marsikaj čudnega.

Vendar pa v sodobnem šolskem kurikulumu matematike kompleksnih števil skoraj nikoli ne najdemo. Iz večine učbenikov so bili izpuščeni, ker naši uradniki menijo, da je tema "pretežka za razumevanje".

To je vse. V naslednji lekciji si bomo ogledali vse ključne lastnosti korenov in se končno naučili, kako poenostaviti iracionalne izraze. :)