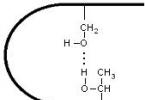
Trigonometrike funksione periodike, pra përsëriten pas një periudhe të caktuar. Si rezultat, mjafton të studiohet funksioni në këtë interval dhe të zgjerohen vetitë e zbuluara në të gjitha periudhat e tjera.

Udhëzimet

1. Nëse ju jepet një shprehje primitive në të cilën ka vetëm një funksion trigonometrik (sin, cos, tg, ctg, sec, cosec), dhe këndi brenda funksionit nuk shumëzohet me asnjë numër, dhe ai vetë nuk është ngritur në asnjë fuqia - përdorni përkufizimin. Për shprehjet që përmbajnë sin, cos, sec, cosec, vendosni me guxim periudhën në 2P, dhe nëse ekuacioni përmban tg, ctg, atëherë P. Le të themi, për funksionin y=2 sinx+5, periudha do të jetë e barabartë me 2P .

2. Nëse këndi x nën shenjën e një funksioni trigonometrik shumëzohet me një numër, atëherë për të gjetur periudhën e këtij funksioni, pjesëtoni periodën tipike me këtë numër. Le të themi se ju është dhënë një funksion y = sin 5x. Periudha tipike për një sinus është 2P; duke e ndarë atë me 5, ju merrni 2P/5 - kjo është periudha e dëshiruar e kësaj shprehjeje.

3. Për të gjetur periudhën e një funksioni trigonometrik të ngritur në një fuqi, vlerësoni barazinë e fuqisë. Për një shkallë të barabartë, zvogëloni periudhën tipike përgjysmë. Le të themi, nëse ju jepet funksioni y = 3 cos^2x, atëherë periudha tipike 2P do të zvogëlohet me 2 herë, kështu që periudha do të jetë e barabartë me P. Ju lutemi vini re se funksionet tg, ctg janë periodike ndaj P për çdo shkallë.

4. Nëse ju jepet një ekuacion që përmban produktin ose herësin e dy funksioneve trigonometrike, së pari gjeni periodën për të gjithë veçmas. Pas kësaj, gjeni numrin minimal që do të përmbajë numrin e plotë të të dy periudhave. Le të themi se është dhënë funksioni y=tgx*cos5x. Për tangjentën perioda është P, për kosinusin 5x perioda është 2P/5. Numri minimal në të cilin mund të akomodohen të dyja këto periudha është 2P, pra periudha e dëshiruar është 2P.

5. Nëse e keni të vështirë ta bëni atë në mënyrën e sugjeruar ose dyshoni në rezultatin, përpiquni ta bëni atë sipas definicionit. Merrni T si periudhë të funksionit; është më i madh se zero. Zëvendësoni shprehjen (x + T) në vend të x në ekuacion dhe zgjidhni barazinë që rezulton sikur T të ishte një parametër ose një numër. Si rezultat, do të zbuloni vlerën e funksionit trigonometrik dhe do të jeni në gjendje të gjeni periodën më të vogël. Le të themi, si rezultat i lehtësimit, ju merrni mëkatin e identitetit (T/2) = 0. Vlera minimale e T në të cilën kryhet është 2P, ky do të jetë rezultati i detyrës.

Një funksion periodik është një funksion që përsërit vlerat e tij pas një periudhe jo zero. Periudha e një funksioni është një numër që, kur i shtohet argumentit të një funksioni, nuk e ndryshon vlerën e funksionit.

Do t'ju duhet

• Njohuri të matematikës elementare dhe rishikim bazë.

Udhëzimet

1. Le të shënojmë periudhën e funksionit f(x) me numrin K. Detyra jonë është të zbulojmë këtë vlerë të K. Për ta bërë këtë, imagjinoni që funksionin f(x), duke përdorur përkufizimin e një funksioni periodik, e barazojmë f(x+K)=f(x).

2. E zgjidhim ekuacionin që rezulton në lidhje me të panjohurën K, sikur x të ishte një konstante. Në varësi të vlerës së K, do të ketë disa opsione.

3. Nëse K>0 – atëherë kjo është periudha e funksionit tuaj.Nëse K=0 – atëherë funksioni f(x) nuk është periodik.Nëse zgjidhja e ekuacionit f(x+K)=f(x) nuk ekziston për çdo K jo të barabartë me zero, atëherë një funksion i tillë quhet aperiodik dhe gjithashtu nuk ka periodë.

Video mbi temën

Shënim!
Të gjitha funksionet trigonometrike janë periodike, dhe të gjitha funksionet polinomiale me një shkallë më të madhe se 2 janë aperiodike.

Këshilla të dobishme
Periudha e një funksioni të përbërë nga 2 funksione periodike është shumëfishi më i vogël universal i periudhave të këtyre funksioneve.

Ekuacionet trigonometrike janë ekuacione që përmbajnë funksione trigonometrike të një argumenti të panjohur (për shembull: 5sinx-3cosx =7). Për të mësuar se si t'i zgjidhni ato, duhet të dini disa mënyra për ta bërë këtë.

Udhëzimet

1. Zgjidhja e ekuacioneve të tilla përbëhet nga 2 faza: E para është reformimi i ekuacionit për të marrë formën e tij më të thjeshtë. Ekuacionet trigonometrike më të thjeshta janë: Sinx=a; Cosx=a etj.

2. E dyta është zgjidhja e ekuacionit më të thjeshtë trigonometrik të marrë. Ekzistojnë mënyra themelore për zgjidhjen e ekuacioneve të këtij lloji: Zgjidhja në mënyrë algjebrike. Kjo metodë është e njohur nga shkolla, nga një kurs algjebër. Quhet ndryshe metoda e zëvendësimit dhe zëvendësimit të variablave. Duke përdorur formulat e reduktimit, ne transformojmë, bëjmë një zëvendësim dhe më pas gjejmë rrënjët.

3. Faktorizimi i një ekuacioni. Së pari, ne i lëvizim të gjithë termat në të majtë dhe i faktorizojmë ato.

4. Reduktimi i ekuacionit në një homogjen. Ekuacionet quhen ekuacione homogjene nëse të gjithë termat janë të së njëjtës shkallë dhe sinusi dhe kosinusi i të njëjtit kënd.Për ta zgjidhur atë duhet: së pari të transferoni të gjithë termat e tij nga ana e djathtë në anën e majtë; zhvendosni të gjithë faktorët universalë jashtë kllapave; barazoni faktorët dhe kllapat me zero; kllapat e barazuara japin një ekuacion homogjen të një shkalle më të ulët, i cili duhet të ndahet me cos (ose sin) në shkallën më të lartë; zgjidhni ekuacionin algjebrik që rezulton në lidhje me tan.

5. Mënyra tjetër është të lëvizni në një kënd gjysmë. Thuaj, zgjidhni ekuacionin: 3 sin x – 5 cos x = 7. Le të kalojmë në gjysmëkëndin: 6 sin (x / 2) · cos (x / 2) - 5 cos? (x / 2) + 5 mëkat ? (x / 2) = 7 mëkat ? (x / 2) + 7 cos ? (x/ 2) , pas së cilës i zvogëlojmë të gjithë termat në një pjesë (mundësisht në anën e djathtë) dhe zgjidhim ekuacionin.

6. Hyrja e këndit ndihmës. Kur zëvendësojmë vlerën e plotë cos(a) ose sin(a). Shenja "a" është një kënd ndihmës.

7. Një metodë e transformimit të një produkti në një shumë. Këtu ju duhet të aplikoni formulat e duhura. Le të themi të dhëna: 2 sin x · sin 3x = cos 4x Zgjidheni duke e shndërruar anën e majtë në një shumë, pra: cos 4x – cos 8x = cos 4x ,cos 8x = 0 ,8x = p / 2 + pk , x = p / 16 + pk / 8.

8. Metoda e fundit quhet zëvendësim me shumë funksione. Transformojmë shprehjen dhe bëjmë një ndryshim, themi Cos(x/2)=u, dhe më pas zgjidhim ekuacionin me parametrin u. Kur blejmë totalin, ne e kthejmë vlerën në të kundërtën.

Video mbi temën

Nëse marrim parasysh pikat në një rreth, atëherë pikat x, x + 2π, x + 4π, etj. përkojnë me njëra-tjetrën. Kështu, trigonometrike funksione në një vijë të drejtë periodikisht përsërisin kuptimin e tyre. Nëse periudha është e famshme funksione, është e mundur të ndërtohet një funksion në këtë periudhë dhe të përsëritet në të tjerat.

Udhëzimet

1. Periudha është një numër T i tillë që f(x) = f(x+T). Për të gjetur periodën, zgjidhni ekuacionin përkatës, duke zëvendësuar x dhe x+T si argument. Në këtë rast, ata përdorin periudhat tashmë të njohura për funksionet. Për funksionet sinus dhe kosinus perioda është 2π, dhe për funksionet tangjente dhe kotangjente është π.

2. Le të jepet funksioni f(x) = sin^2(10x). Konsideroni shprehjen sin^2(10x) = sin^2(10(x+T)). Përdorni formulën për të zvogëluar shkallën: sin^2(x) = (1 – cos 2x)/2. Pastaj ju merrni 1 – cos 20x = 1 – cos 20 (x+T) ose cos 20x = cos (20x+20T). Duke ditur se periudha e kosinusit është 2π, 20T = 2π. Kjo do të thotë T = π/10. T është periudha minimale e saktë, dhe funksioni do të përsëritet pas 2T, dhe pas 3T, dhe në drejtimin tjetër përgjatë boshtit: -T, -2T, etj.

Këshilla të dobishme
Përdorni formula për të zvogëluar shkallën e një funksioni. Nëse i dini tashmë periudhat e disa funksioneve, përpiquni ta reduktoni funksionin ekzistues në ato të njohura.

Shqyrtimi i një funksioni për barazi dhe çuditshmëri ndihmon për të ndërtuar një grafik të funksionit dhe për të kuptuar natyrën e sjelljes së tij. Për këtë hulumtim, ju duhet të krahasoni këtë funksion të shkruar për argumentin "x" dhe për argumentin "-x".

Udhëzimet

1. Shkruani funksionin që dëshironi të hetoni në formën y=y(x).

2. Zëvendësoni argumentin e funksionit me “-x”. Zëvendësoni këtë argument në një shprehje funksionale.

3. Thjeshtoni shprehjen.

4. Kështu, ju keni të njëjtin funksion të shkruar për argumentet "x" dhe "-x". Shikoni këto dy hyrje: Nëse y(-x)=y(x), atëherë është një funksion çift. Nëse y(-x)=-y(x), atëherë është një funksion tek. Nëse është e pamundur të themi për një funksion që y (-x)=y(x) ose y(-x)=-y(x), atëherë nga vetia e barazisë ky është një funksion i formës universale. Domethënë nuk është as çift dhe as tek.

5. Shkruani gjetjet tuaja. Tani ju mund t'i përdorni ato në ndërtimin e një grafiku të një funksioni ose në një studim analitik të ardhshëm të vetive të një funksioni.

6. Është gjithashtu e mundur të flitet për njëtrajtësinë dhe çuditshmërinë e një funksioni në rastin kur grafiku i funksionit është dhënë tashmë. Le të themi se grafiku shërbeu si rezultat i një eksperimenti fizik.Nëse grafiku i një funksioni është simetrik në lidhje me boshtin e ordinatave, atëherë y(x) është një funksion çift.Nëse grafiku i një funksioni është simetrik në lidhje me boshtin e abshisës, atëherë x(y) është një funksion çift. x(y) është një funksion i anasjelltë me funksionin y(x) Nëse grafiku i një funksioni është simetrik me origjinën (0,0), atëherë y(x) është një funksion tek. Funksioni i anasjelltë x(y) gjithashtu do të jetë tek.

7. Është e rëndësishme të mbani mend se ideja e çiftësisë dhe e çuditshmërisë së një funksioni ka një lidhje të drejtpërdrejtë me domenin e përkufizimit të funksionit. Nëse, të themi, një funksion çift ose tek nuk ekziston në x=5, atëherë ai nuk ekziston në x=-5, gjë që nuk mund të thuhet për një funksion të një forme universale. Kur vendosni barazinë çift dhe tek, kushtojini vëmendje domenit të funksionit.

8. Gjetja e një funksioni për barazinë dhe çuditshmërinë lidhet me gjetjen e një grupi vlerash funksioni. Për të gjetur grupin e vlerave të një funksioni çift, mjafton të shikoni gjysmën e funksionit, në të djathtë ose në të majtë të zeros. Nëse në x>0 funksioni çift y(x) merr vlera nga A në B, atëherë do të marrë të njëjtat vlera në x<0.Для нахождения множества значений, принимаемых нечетной функцией, тоже довольно разглядеть только одну часть функции. Если при x>Funksioni 0 tek y(x) merr një varg vlerash nga A në B, pastaj në x<0 она будет принимать симметричный диапазон значений от (-В) до (-А).

"Trigonometrike" dikur filluan të quheshin funksione që përcaktohen nga varësia e këndeve akute në një trekëndësh kënddrejtë nga gjatësitë e brinjëve të tij. Funksione të tilla përfshijnë, para së gjithash, sinusin dhe kosinusin, së dyti, inversin e këtyre funksioneve, sekant dhe kosekant, derivatet e tyre tangjente dhe kotangjente, si dhe funksionet e anasjellta të arksinës, arkosinës etj. Është më pozitive të mos flasim për "zgjidhja" e funksioneve të tilla, por për "llogaritjen" e tyre, domethënë për gjetjen e një vlere numerike.

Udhëzimet

1. Nëse argumenti i funksionit trigonometrik është i panjohur, atëherë vlera e tij mund të llogaritet me një metodë indirekte bazuar në përkufizimet e këtyre funksioneve. Për ta bërë këtë, ju duhet të dini gjatësitë e brinjëve të trekëndëshit, funksioni trigonometrik për një nga këndet e të cilit duhet të llogaritet. Le të themi, sipas përkufizimit, sinusi i një këndi akut në një trekëndësh kënddrejtë është raporti i gjatësisë së këmbës përballë këtij këndi me gjatësinë e hipotenuzës. Nga kjo rezulton se për të gjetur sinusin e një këndi mjafton të dimë gjatësitë e këtyre 2 brinjëve. Një përkufizim i ngjashëm thotë se sinusi i një këndi akut është raporti i gjatësisë së këmbës ngjitur me këtë kënd me gjatësinë e hipotenuzës. Tangjentja e një këndi akut mund të llogaritet duke pjesëtuar gjatësinë e këmbës së kundërt me gjatësinë e asaj ngjitur, dhe kotangjentja kërkon pjesëtimin e gjatësisë së këmbës ngjitur me gjatësinë e këmbës së kundërt. Për të llogaritur sekantin e një këndi akut, duhet të gjeni raportin e gjatësisë së hipotenuzës me gjatësinë e këmbës ngjitur me këndin e kërkuar, dhe kosekanti përcaktohet nga raporti i gjatësisë së hipotenuzës me gjatësinë. të këmbës së kundërt.

2. Nëse argumenti i funksionit trigonometrik është i saktë, atëherë nuk keni nevojë të dini gjatësitë e anëve të trekëndëshit - mund të përdorni tabela vlerash ose kalkulatorë të funksioneve trigonometrike. Një kalkulator i tillë përfshihet në programet standarde të sistemit operativ Windows. Për ta nisur atë, mund të shtypni kombinimin e tastit Win + R, futni komandën calc dhe klikoni butonin "OK". Në ndërfaqen e programit, duhet të zgjeroni seksionin "Shiko" dhe të zgjidhni artikullin "Inxhinier" ose "Shkencëtar". Pas kësaj, është e mundur të prezantohet argumenti i funksionit trigonometrik. Për të llogaritur funksionet sinus, kosinus dhe tangjentë, më mirë pasi të keni futur vlerën, klikoni në butonin përkatës të ndërfaqes (sin, cos, tg) dhe për të gjetur harkun e kundërt, arkozinën dhe arktangjenten e tyre, duhet të kontrolloni paraprakisht kutinë e kontrollit Inv.

3. Ka edhe metoda alternative. Një prej tyre është të shkoni në faqen e internetit të motorit të kërkimit Nigma ose Google dhe të futni funksionin e dëshiruar dhe argumentin e tij si një pyetje kërkimi (të themi, sin 0.47). Këta motorë kërkimi kanë kalkulatorë të integruar, kështu që pas dërgimit të një kërkese të tillë do të merrni vlerën e funksionit trigonometrik që keni futur.

Video mbi temën

Këshilla 7: Si të zbuloni vlerën e funksioneve trigonometrike

Funksionet trigonometrike u shfaqën për herë të parë si mjete për llogaritjet abstrakte matematikore të varësive të vlerave të këndeve akute në një trekëndësh kënddrejtë në gjatësitë e brinjëve të tij. Tani ato përdoren gjerësisht në fushat shkencore dhe teknike të veprimtarisë njerëzore. Për llogaritjet utilitare të funksioneve trigonometrike nga argumentet e dhëna, mund të përdorni mjete të ndryshme - disa prej tyre që janë veçanërisht të arritshme përshkruhen më poshtë.

Udhëzimet

1. Përdorni, le të themi, programin llogaritës të instaluar si parazgjedhje me sistemin operativ. Hapet duke zgjedhur artikullin "Llogaritësi" në dosjen "Shërbimi" nga nënseksioni "Tipik", i vendosur në seksionin "Të gjitha programet". Ky seksion mund të gjendet duke hapur menunë kryesore të sistemit operativ duke klikuar në butonin "Start". Nëse jeni duke përdorur versionin e Windows 7, atëherë ka të ngjarë që thjesht të futni fjalën "Llogaritësi" në fushën "Zbuloni programet dhe skedarët" të menysë kryesore dhe më pas klikoni në lidhjen përkatëse në rezultatet e kërkimit.

2. Futni vlerën e këndit për të cilin dëshironi të llogaritni funksionin trigonometrik dhe më pas klikoni në butonin që korrespondon me këtë funksion - sin, cos ose tan. Nëse jeni të shqetësuar për funksionet trigonometrike të anasjellta (sinusi i harkut, kosinusi i harkut ose tangjenta e harkut), atëherë së pari klikoni butonin e emërtuar Inv - ai kthen funksionet e caktuara në butonat udhëzues të makinës llogaritëse.

3. Në versionet e mëparshme të OS (të themi, Windows XP), për të hyrë në funksionet trigonometrike, duhet të hapni seksionin "Shiko" në menynë e kalkulatorit dhe të zgjidhni linjën "Inxhinieri". Për më tepër, në vend të butonit Inv, ndërfaqja e versioneve më të vjetra të programit ka një kuti kontrolli me të njëjtin mbishkrim.

4. Ju mund të bëni pa një kalkulator nëse keni akses në internet. Ka shumë shërbime në internet që ofrojnë kalkulatorë të funksioneve trigonometrike të organizuar në mënyra të ndryshme. Një nga opsionet veçanërisht të përshtatshme është i integruar në motorin e kërkimit Nigma. Duke shkuar në faqen e tij kryesore, thjesht futni vlerën që ju shqetëson në fushën e pyetjes së kërkimit - të themi, "hark tangjent 30 gradë". Pasi të klikoni në butonin "Zbuloni!" Motori i kërkimit do të llogarisë dhe do të tregojë rezultatin e llogaritjes - 0.482347907101025.

Video mbi temën

Trigonometria është një degë e matematikës për të kuptuar funksionet që shprehin varësi të ndryshme të brinjëve të një trekëndëshi kënddrejtë nga vlerat e këndeve akute në hipotenuzë. Funksione të tilla quheshin trigonometrike dhe për të lehtësuar punën me to, u nxorrën funksione trigonometrike identitetet .

Performanca identitetet në matematikë tregon një barazi që plotësohet për të gjitha vlerat e argumenteve të funksioneve të përfshira në të. Trigonometrike identitetet janë barazi funksionesh trigonometrike, të konfirmuara dhe të pranuara për të thjeshtuar punën me formulat trigonometrike.Funksioni trigonometrik është një funksion elementar i varësisë së njërës nga këmbët e një trekëndëshi kënddrejtë nga vlera e këndit akut në hipotenuzë. Gjashtë funksionet bazë trigonometrike që përdoren më shpesh janë sin (sinus), cos (kosinus), tg (tangent), ctg (kotangjent), sec (sekant) dhe cosec (kosekant). Këto funksione quhen funksione të drejtpërdrejta, ka edhe funksione të anasjellta, le të themi, sinus - arksin, kosinus - arkozin etj. Fillimisht funksionet trigonometrike u pasqyruan në gjeometri, pas së cilës u përhapën në fusha të tjera të shkencës: fizikë, kimi, gjeografi, etj. optika, teoria e probabilitetit, si dhe akustika, teoria e muzikës, fonetika, grafika kompjuterike dhe shumë të tjera. Në ditët e sotme është e vështirë të imagjinohen llogaritjet matematikore pa këto funksione, megjithëse në të kaluarën e largët ato përdoreshin vetëm në astronomi dhe arkitekturë.Trigonometrike identitetet përdoren për të thjeshtuar punën me formula të gjata trigonometrike dhe për t'i reduktuar në një formë të tretshme. Ekzistojnë gjashtë identitete kryesore trigonometrike; ato lidhen me funksionet e drejtpërdrejta trigonometrike: tg ? = mëkat?/cos?; mëkat^2? +cos^2? = 1; 1 + tg^2? = 1/cos^2?; 1 + 1/tg^2? = 1/mëkat^2?; sin (?/2 – ?) = cos ?; cos (?/2 – ?) = mëkat ?. Këto identitetet lehtë për t'u konfirmuar nga vetitë e raportit të brinjëve dhe këndeve në një trekëndësh kënddrejtë: mëkat ? = BC/AC = b/c; cos? = AB/AC = a/c; tg? = b/a Identiteti i parë tg ? = mëkat ?/cos ? rrjedh nga raporti i brinjëve në trekëndësh dhe përjashtimi i brinjës c (hipotenuzës) kur pjesëtohet mëkati me cos. Identiteti ctg? është përcaktuar në të njëjtën mënyrë. = cos ?/sin ?, sepse ctg ? = 1/tg ?. Nga teorema e Pitagorës a^2 + b^2 = c^2. Le ta ndajmë këtë barazi me c^2, marrim identitetin e dytë: a^2/c^2 + b^2/c^2 = 1 => sin^2 ? + cos^2 ? = 1.E treta dhe e katërta identitetet përftohet duke pjesëtuar, përkatësisht, me b^2 dhe a^2: a^2/b^2 + 1 = c^2/b^2 => tg^2 ? + 1 = 1/cos^2 ?;1 + b^2/a^2 = c^2/a^2 => 1 + 1/tg^2 ? = 1/mëkat^ ? apo 1 + ctg^2 ? = 1/sin^2 ?. E pesta dhe e gjashta bazë identitetet vërtetohen duke përcaktuar shumën e këndeve akute të një trekëndëshi kënddrejtë, e cila është e barabartë me 90° ose?/2.Më e vështirë trigonometrike identitetet: formulat për mbledhjen e argumenteve, këndeve të dyfishta dhe të trefishta, zvogëlimin e shkallëve, reformimin e shumës ose prodhimit të funksioneve, si dhe formulat për zëvendësimin trigonometrik, përkatësisht shprehjet e funksioneve bazë trigonometrike përmes tg të një gjysmë këndi: sin ?= (2*tg ?/2)/(1 + tan^2 ?/2);cos ? = (1 – tg^2 ?/2)/(1 = tg^2 ?/2);tg ? = (2*tg ?/2)/(1 – tg^2 ?/2).

Nevoja për të gjetur minimumin kuptimi matematikore funksioneështë me interes aktual për zgjidhjen e problemeve të aplikuara, të themi, në ekonomi. I madh kuptimi minimizimi i humbjeve është thelbësor për aktivitetet e biznesit.

Udhëzimet

1. Për të zbuluar minimumin kuptimi funksione, është e nevojshme të përcaktohet se në cilën vlerë të argumentit x0 do të plotësohet pabarazia y(x0)? y(x), ku x? x0. Si zakonisht, ky problem zgjidhet në një interval të caktuar ose në çdo varg vlerash funksione, nëse një nuk është specifikuar. Një aspekt i zgjidhjes është gjetja e pikave fikse.

2. Një pikë e palëvizshme quhet kuptimi argument në të cilin derivati funksione shkon në zero. Sipas teoremës së Fermatit, nëse një funksion i diferencueshëm merr një ekstrem kuptimi në një moment (në këtë rast, një minimum lokal), atëherë kjo pikë është e palëvizshme.

3. Minimumi kuptimi funksioni shpesh merr pikërisht këtë pikë, por ai nuk mund të përcaktohet pa ndryshim. Për më tepër, nuk është gjithmonë e mundur të thuhet me saktësi se cili është minimumi funksione ose e pranon të voglën pafundësisht kuptimi. Pastaj, si zakonisht, ata gjejnë kufirin në të cilin priret ndërsa zvogëlohet.

4. Për të përcaktuar minimumin kuptimi funksione, ju duhet të kryeni një sekuencë veprimesh të përbërë nga katër faza: gjetja e domenit të përkufizimit funksione, marrja e pikave fikse, pasqyra e vlerave funksione në këto pika dhe në skajet e hendekut, duke zbuluar minimumin.

5. Rezulton se një funksion y(x) është dhënë në një interval me kufij në pikat A dhe B. Gjeni domenin e përkufizimit të tij dhe zbuloni nëse intervali është nëngrupi i tij.

6. Llogaritni derivatin funksione. Barazoni shprehjen që rezulton me zero dhe gjeni rrënjët e ekuacionit. Kontrolloni nëse këto pika të palëvizshme bien brenda hendekut. Nëse jo, atëherë ato nuk merren parasysh në një fazë të mëtejshme.

7. Shqyrtoni boshllëkun për llojin e kufijve: të hapur, të mbyllur, të përbërë ose të pamatshëm. Kjo përcakton se si kërkoni minimumin kuptimi. Le të themi se segmenti [A, B] është një interval i mbyllur. Futni ato në funksion dhe llogaritni vlerat. Bëni të njëjtën gjë me një pikë të palëvizshme. Zgjidhni totalin më të ulët.

8. Me intervale të hapura dhe të pamatshme situata është disi më e vështirë. Këtu do të duhet të kërkoni kufizime të njëanshme që nuk japin pa ndryshim një rezultat të paqartë. Le të themi, për një interval me një kufi të mbyllur dhe një kufi të shpuar [A, B), duhet të gjendet një funksion në x = A dhe një kufi i njëanshëm lim y në x? B-0.

Argumenti x, atëherë quhet periodik nëse ka një numër T të tillë që për çdo x F(x + T) = F(x). Ky numër T quhet periudha e funksionit.

Mund të ketë disa periudha. Për shembull, funksioni F = const merr të njëjtën vlerë për çdo vlerë të argumentit, dhe për këtë arsye çdo numër mund të konsiderohet perioda e tij.

Zakonisht ju intereson periudha më e vogël jozero e një funksioni. Për shkurtësi, quhet thjesht një periudhë.

Një shembull klasik i funksioneve periodike është trigonometrik: sinus, kosinus dhe tangent. Periudha e tyre është e njëjtë dhe e barabartë me 2π, domethënë sin(x) = sin(x + 2π) = sin(x + 4π) e kështu me radhë. Megjithatë, sigurisht, funksionet trigonometrike nuk janë të vetmet periodike.

Për funksionet e thjeshta, themelore, mënyra e vetme për të përcaktuar nëse ato janë periodike apo jo periodike është përmes llogaritjes. Por për funksionet komplekse tashmë ekzistojnë disa rregulla të thjeshta.

Nëse F(x) është me periudhën T, dhe për të është përcaktuar një derivat, atëherë ky derivat f(x) = F′(x) është gjithashtu një funksion periodik me periudhën T. Në fund të fundit, vlera e derivatit në pikën x është e barabartë me tangjenten e këndit tangjent të grafikut të antiderivativit të tij në këtë pikë me boshtin x, dhe meqenëse antiderivati ​​përsëritet periodikisht, derivati ​​gjithashtu duhet të përsëritet. Për shembull, derivati ​​i funksionit sin(x) është i barabartë me cos(x), dhe është periodik. Marrja e derivatit të cos(x) ju jep –sin(x). Frekuenca mbetet e pandryshuar.

Megjithatë, e kundërta nuk është gjithmonë e vërtetë. Kështu, funksioni f(x) = konst është periodik, por antiderivativi i tij F(x) = konst*x + C nuk është.

Nëse F(x) është një funksion periodik me periudhë T, atëherë G(x) = a*F(kx + b), ku a, b dhe k janë konstante dhe k nuk është e barabartë me zero - është gjithashtu një funksion periodik. , dhe periudha e saj është T/k. Për shembull, sin(2x) është një funksion periodik, dhe periudha e tij është π. Kjo mund të paraqitet vizualisht si më poshtë: duke shumëzuar x me një numër, ju duket se e ngjeshni grafikun e funksionit horizontalisht pikërisht kaq shumë herë

Nëse F1(x) dhe F2(x) janë funksione periodike, dhe periodat e tyre janë përkatësisht të barabarta me T1 dhe T2, atëherë shuma e këtyre funksioneve mund të jetë edhe periodike. Megjithatë, periudha e saj nuk do të jetë një shumë e thjeshtë e periudhave T1 dhe T2. Nëse rezultati i pjesëtimit T1/T2 është një numër racional, atëherë shuma e funksioneve është periodike dhe periudha e saj është e barabartë me shumëfishin më të vogël të përbashkët (LCM) të periudhave T1 dhe T2. Për shembull, nëse periudha e funksionit të parë është 12, dhe periudha e të dytit është 15, atëherë periudha e shumës së tyre do të jetë e barabartë me LCM (12, 15) = 60.

Kjo mund të paraqitet vizualisht si më poshtë: funksionet vijnë me "gjerësi hapash" të ndryshme, por nëse raporti i gjerësisë së tyre është racional, atëherë herët a vonë (ose më mirë, pikërisht përmes LCM-së së hapave), ato do të bëhen përsëri të barabarta, dhe shuma e tyre do të fillojë një periudhë të re.

Megjithatë, nëse raporti i periudhave është irracional, atëherë funksioni total nuk do të jetë fare periodik. Për shembull, le të jetë F1(x) = x mod 2 (mbetja kur x pjesëtohet me 2), dhe F2(x) = sin(x). T1 këtu do të jetë i barabartë me 2, dhe T2 do të jetë i barabartë me 2π. Raporti i periodave është i barabartë me π - një numër irracional. Prandaj, funksioni sin(x) + x mod 2 nuk është periodik.

plotësimi i sistemit të pabarazive:

b) Konsideroni një grup numrash në vijën numerike që plotësojnë sistemin e pabarazive:

Gjeni shumën e gjatësive të segmenteve që përbëjnë këtë bashkësi.

§ 7. Formulat më të thjeshta

Në § 3 vendosëm formulën e mëposhtme për këndet akute α:

			sin2 α + cos2 α = 1.
				E njëjta formulë			kur,
				kur α është ndonjë			në fakt
				le, le të jetë M një pikë në trigonometri
				rrethi ik që korrespondon me
				numri α (Fig. 7.1). Pastaj		M ka bashkë-
				ordinatat x = cos α, y
				Megjithatë, çdo pikë (x; y) shtrihet në
				rrethi i rrezes së njësisë me qendër
				trome në origjinë, të kënaqshme
				plotëson ekuacionin x2 + y2		1, nga
				cos2 α + sin2 α = 1, sipas nevojës.

Pra, formula cos2 α + sin2 α = 1 rrjedh nga ekuacioni i rrethit. Mund të duket se në këtë mënyrë kemi dhënë një provë të re të kësaj formule për këndet akute (në krahasim me atë të treguar në § 3, ku kemi përdorur teoremën e Pitagorës). Dallimi, megjithatë, është thjesht i jashtëm: kur nxjerrim ekuacionin e një rrethi x2 + y2 = 1, përdoret e njëjta teoremë e Pitagorës.

Për këndet akute kemi marrë edhe formula të tjera, p.sh

Sipas simbolit, ana e djathtë është gjithmonë jo negative, ndërsa ana e majtë mund të jetë fare negative. Që formula të jetë e vërtetë për të gjithë α, duhet të jetë katror. Barazia që rezulton është: cos2 α = 1/(1 + tan2 α). Le të vërtetojmë se kjo formulë është e vërtetë për të gjithë α:1

1/(1 + tan2			sin2 α			cos2 α	Cos2 α.
			cos2 α			sin2 α + cos2 α

Problemi 7.1. Nxirrni të gjitha formulat e mëposhtme nga përkufizimet dhe formula sin2 α + cos2 α = 1 (ne kemi vërtetuar tashmë disa prej tyre):

sin2 α + cos2 α = 1;

tg2 α =

tg2 α

sin2 α =

tg α · ctg α = 1;

cos2 α

1 + tan2 α

ctg2 α

Ctg2

cos2 α =

1 + cotg2 α

mëkat2

Këto formula ju lejojnë, duke ditur vlerën e një prej funksioneve trigonometrike të një numri të caktuar, të gjeni pothuajse të gjithë pjesën tjetër.

i ri Le të dimë, për shembull, se sin x = 1/2. Atëherë cos2 x =

1−sin2 x = 3/4, pra cos x është ose 3/2 ose − 3/2. Për të zbuluar se me cilin nga këta dy numra cos x është i barabartë, nevojiten informacione shtesë.

Problemi 7.2. Tregoni me shembuj se të dyja rastet e mësipërme janë të mundshme.

Problemi 7.3. a) Le të jetë tan x = −1. Gjeni mëkatin x. Sa përgjigje ka ky problem?

b) Përveç kushteve të pikës a) le të dimë se sin x< 0. Сколько теперь ответов у задачи?

1 Për të cilën është përcaktuar tan α, d.m.th. cos α 6= 0.

Problemi 7.4. Le të sin x = 3/5, x [π/2; 3π/2]. Gjeni tg x.

Problemi 7.5. Le të jetë tan x = 3, cos x > sin x. Gjeni cos x, sin x.

Problemi 7.6. Le të jetë tg x = 3/5. Gjeni sin x + 2 cos x. cos x − 3 sin x

Problemi 7.7. Vërtetoni identitetin:

tan α − sin α

c) sin α + cos α cot α + sin α tan α + cos α =

Problemi 7.8. Thjeshtoni shprehjet:

a) (sin α + cos α)2 + (sin α − cos α)2 ; b) (tg α + ctg α)2 + (tg α − ctg α)2 ;

c) sin α(2 + cot α)(2 cot α + 1) − 5 cos α.

§ 8. Periudhat e funksioneve trigonometrike

Numrat x, x+2π, x−2π korrespondojnë me të njëjtën pikë në rrethin trigonometrik (nëse ecni një rreth shtesë përgjatë rrethit trigonometrik, do të ktheheni aty ku ishit). Kjo nënkupton identitetet e mëposhtme, të cilat u diskutuan tashmë në § 5:

sin(x + 2π) = mëkat (x − 2π) = mëkat x; cos(x + 2π) = cos(x − 2π) = cos x.

Në lidhje me këto identitete ne kemi përdorur tashmë termin "periudhë". Tani le të japim përkufizime të sakta.

Përkufizimi. Numri T 6= 0 quhet perioda e funksionit f nëse për të gjitha x barazimet f(x − T) = f(x + T) = f(x) janë të vërteta (supozohet se x + T dhe x − T përfshihen në domenin e përkufizimit të funksionit , nëse përfshin x). Një funksion quhet periodik nëse ka një periudhë (të paktën një).

Funksionet periodike lindin natyrshëm kur përshkruhen proceset osciluese. Një nga proceset e tilla është diskutuar tashmë në § 5. Këtu janë më shumë shembuj:

1) Le të jetë ϕ = ϕ(t) këndi i devijimit të lavjerrësit lëkundës të orës nga vertikalja në momentin t. Atëherë ϕ është një funksion periodik i t.

2) Tensioni ("ndryshimi i mundshëm", siç do të thoshte një fizikant) midis dy prizave të një prize AC, është

nëse konsiderohet si funksion i kohës, është një funksion periodik1.

3) Le të dëgjojmë tingullin muzikor. Atëherë presioni i ajrit në një pikë të caktuar është një funksion periodik i kohës.

Nëse një funksion ka një periudhë T, atëherë periodat e këtij funksioni do të jenë edhe numrat −T, 2T, −2T. . . - me një fjalë, të gjithë numrat nT, ku n është një numër i plotë që nuk është i barabartë me zero. Në të vërtetë, le të kontrollojmë, për shembull, që f(x + 2T) = f(x):

f(x + 2T) = f((x + T) + T) = f(x + T) = f(x).

Përkufizimi. Periudha pozitive më e vogël e një funksioni f është - në përputhje me kuptimin e mirëfilltë të fjalëve - një numër pozitiv T i tillë që T është një periudhë e f dhe asnjë numër pozitiv më i vogël se T nuk është një periudhë f.

Një funksion periodik nuk kërkohet të ketë periudhën më të vogël pozitive (për shembull, një funksion që është konstant ka një periudhë të çdo numri fare dhe, për rrjedhojë, nuk ka periudhën më të vogël pozitive). Mund të japim edhe shembuj të funksioneve periodike jo konstante që nuk kanë periudhën më të vogël pozitive. Sidoqoftë, në rastet më interesante, ekziston periudha më e vogël pozitive e funksioneve periodike.

1 Kur thonë "tensioni në rrjet është 220 volt", nënkuptojnë "vlerën rms" të tij, për të cilën do të flasim në § 21. Vetë tensioni ndryshon gjatë gjithë kohës.

Oriz. 8.1. Periudha e tangjentes dhe kotangjentes.

Në veçanti, periudha më e vogël pozitive e sinusit dhe kosinusit është 2π. Le ta vërtetojmë këtë, për shembull, për funksionin y = sin x. Le të, ndryshe nga sa pretendojmë, sinusi ka një periudhë T të tillë që 0< T < 2π. При x = π/2 имеем sin x = = 1. Будем теперь увеличивать x. В точке x + T значение синуса должно быть также равно 1. Но в следующий раз синус будет равен 1 только при x = (π/2) + 2π. Поэтому период синуса быть меньше 2π не может. Доказательство для косинуса аналогично.

Periudha më e vogël pozitive e funksionit që përshkruan lëkundjet (si në shembujt tanë 1-3) quhet thjesht periudha e këtyre lëkundjeve.

Meqenëse 2π është periudha e sinusit dhe kosinusit, do të jetë gjithashtu periudha e tangjentes dhe kotangjentës. Megjithatë, për këto funksione, 2π nuk është periudha më e vogël: periudha më e vogël pozitive e tangjentës dhe kotangjentës do të jetë π. Në fakt, pikat që korrespondojnë me numrat x dhe x + π në rrethin trigonometrik janë diametralisht të kundërta: nga pika x në pikën x + 2π duhet të përshkohet një distancë π saktësisht e barabartë me gjysmën e rrethit. Tani, nëse përdorim përkufizimin e tangjentes dhe kotangjentes duke përdorur boshtet e tangjentëve dhe kotangjenteve, barazitë tg(x + π) = tan x dhe ctg(x + π) = ctg x do të bëhen të dukshme (Fig. 8.1). Është e lehtë të kontrollohet (do të sugjerojmë ta bëjmë këtë në problema) që π është me të vërtetë periudha më e vogël pozitive e tangjentes dhe kotangjentes.

Një shënim për terminologjinë. Fjalët "periudha e një funksioni" përdoren shpesh për të nënkuptuar "periudhën më të vogël pozitive". Pra, nëse në një provim pyeteni: “A është 100π periudha e funksionit të sinusit?”, mos nxitoni të përgjigjeni, por sqaroni nëse keni parasysh periudhën më të vogël pozitive apo vetëm një nga periodat.

Funksionet trigonometrike janë një shembull tipik i funksioneve periodike: çdo funksion periodik "jo shumë i keq" në një farë kuptimi mund të shprehet në terma të atyre trigonometrikë.

Problemi 8.1. Gjeni periudhat më të vogla pozitive të funksioneve:

				c) y = cos πx;

d) y = cos x + cos(1.01x).

Problemi 8.2. Varësia e tensionit në një rrjet të rrymës alternative nga koha jepet me formulën U = U0 sin ωt (këtu t është koha, U është tension, U0 dhe ω janë konstante). Frekuenca e rrymës alternative është 50 Hertz (kjo do të thotë se voltazhi bën 50 lëkundje në sekondë).

a) Gjeni ω, duke supozuar se t matet në sekonda;

b) Gjeni periodën (më të vogël pozitive) të U-së në funksion të t.

Problemi 8.3. a) Vërtetoni se periudha më e vogël pozitive e kosinusit është 2π;

b) Vërtetoni se periudha më e vogël pozitive e tangjentes është e barabartë me π.

Problemi 8.4. Le të jetë periudha më e vogël pozitive e funksionit f të jetë T. Vërtetoni se të gjitha periudhat e tjera të tij janë të formës nT për disa numra të plotë n.

Problemi 8.5. Vërtetoni se funksionet e mëposhtme nuk janë periodike.

Qëllimi: të përmbledhë dhe të sistemojë njohuritë e nxënësve për temën "Periodiciteti i funksioneve"; të zhvillojë aftësi në zbatimin e vetive të një funksioni periodik, gjetjen e periudhës më të vogël pozitive të një funksioni, ndërtimin e grafikëve të funksioneve periodike; nxisin interesin për studimin e matematikës; kultivojnë vëzhgimin dhe saktësinë.

Pajisjet: kompjuter, projektor multimedial, karta detyrash, rrëshqitje, orë, tabela stoli, elemente të zejeve popullore

"Matematika është ajo që njerëzit përdorin për të kontrolluar natyrën dhe veten."
A.N. Kolmogorov

Gjatë orëve të mësimit

I. Faza organizative.

Kontrollimi i gatishmërisë së nxënësve për mësimin. Raportoni temën dhe objektivat e mësimit.

II. Kontrollimi i detyrave të shtëpisë.

Ne kontrollojmë detyrat e shtëpisë duke përdorur mostra dhe diskutojmë pikat më të vështira.

III. Përgjithësimi dhe sistematizimi i njohurive.

1. Punë ballore gojore.

Çështjet e teorisë.

1) Formoni një përkufizim të periudhës së funksionit
2) Emërtoni periudhën më të vogël pozitive të funksioneve y=sin(x), y=cos(x)
3). Cila është periudha më e vogël pozitive e funksioneve y=tg(x), y=ctg(x)
4) Duke përdorur një rreth, provoni korrektësinë e marrëdhënieve:

y=sin(x) = sin(x+360º)
y=cos(x) = cos(x+360º)
y=tg(x) = tg(x+18 0º)
y=ctg(x) = ctg(x+180º)

tg(x+π n)=tgx, n € Z
ctg(x+π n)=ctgx, n € Z

sin(x+2π n)=sinx, n € Z
cos(x+2π n)=cosx, n € Z

5) Si të vizatoni një funksion periodik?

Ushtrime me gojë.

1) Provoni marrëdhëniet e mëposhtme

a) mëkat (740º) = mëkat (20º)
b) cos(54º) = cos(-1026º)
c) sin (-1000º) = mëkat (80º)

2. Vërtetoni se një kënd prej 540º është një nga periodat e funksionit y= cos(2x)

3. Vërtetoni se këndi 360º është një nga periodat e funksionit y=tg(x)

4. Shndërrojini këto shprehje në mënyrë që këndet e përfshira në to të mos kalojnë 90º në vlerë absolute.

a) tg375º
b) ctg530º
c) mëkat1268º
d) cos(-7363º)

5. Ku i keni hasur fjalët PERIUDHË, PERIODICITE?

Nxënësi përgjigjet: Një periudhë në muzikë është një strukturë në të cilën paraqitet një mendim muzikor pak a shumë i plotë. Një periudhë gjeologjike është pjesë e një epoke dhe ndahet në epoka me një periudhë nga 35 deri në 90 milionë vjet.

Gjysma e jetës së një lënde radioaktive. Thyesë periodike. Revista periodike janë botime të shtypura që shfaqen brenda afateve të përcaktuara rreptësisht. Sistemi periodik i Mendelejevit.

6. Në figura janë paraqitur pjesë të grafikëve të funksioneve periodike. Përcaktoni periudhën e funksionit. Përcaktoni periudhën e funksionit.

Përgjigju: T=2; T=2; T=4; T=8.

7. Ku e keni hasur në jetën tuaj ndërtimin e elementeve përsëritëse?

Përgjigja e nxënësit: Elemente stoli, art popullor.

IV. Zgjidhja kolektive e problemeve.

(Zgjidhja e problemeve në sllajde.)

Le të shqyrtojmë një nga mënyrat për të studiuar një funksion për periodicitet.

Kjo metodë shmang vështirësitë që lidhen me vërtetimin se një periudhë e caktuar është më e vogla, dhe gjithashtu eliminon nevojën për të prekur pyetje në lidhje me veprimet aritmetike mbi funksionet periodike dhe periodicitetin e një funksioni kompleks. Arsyetimi bazohet vetëm në përcaktimin e një funksioni periodik dhe në faktin vijues: nëse T është periudha e funksionit, atëherë nT(n?0) është periudha e tij.

Detyra 1. Gjeni periodën më të vogël pozitive të funksionit f(x)=1+3(x+q>5)

Zgjidhje: Supozojmë se periudha T e këtij funksioni. Atëherë f(x+T)=f(x) për të gjitha x € D(f), d.m.th.

1+3(x+T+0.25)=1+3(x+0.25)
(x+T+0.25)=(x+0.25)

Le të vendosim x=-0,25 marrim

(T)=0<=>T=n, n € Z

Ne kemi marrë se të gjitha periudhat e funksionit në fjalë (nëse ekzistojnë) janë ndër numrat e plotë. Le të zgjedhim numrin më të vogël pozitiv midis këtyre numrave. Kjo 1 . Le të kontrollojmë nëse do të jetë me të vërtetë një periudhë 1 .

f(x+1) =3(x+1+0.25)+1

Meqenëse (T+1)=(T) për çdo T, atëherë f(x+1)=3((x+0.25)+1)+1=3(x+0.25)+1=f(x), d.m.th. 1 – periudha f. Meqenëse 1 është më i vogli nga të gjithë numrat e plotë pozitiv, atëherë T=1.

Detyra 2. Tregoni se funksioni f(x)=cos 2 (x) është periodik dhe gjeni periodën e tij kryesore.

Problemi 3. Gjeni periudhën kryesore të funksionit

f(x)=sin(1.5x)+5cos(0.75x)

Le të supozojmë periudhën T të funksionit, pastaj për cilindo X raporti është i vlefshëm

sin1.5(x+T)+5cos0.75(x+T)=sin(1.5x)+5cos(0.75x)

Nëse x=0, atëherë

sin(1.5T)+5cos(0.75T)=sin0+5cos0

sin(1.5T)+5cos(0.75T)=5

Nëse x=-T, atëherë

sin0+5cos0=sin(-1.5T)+5cos0.75(-T)

5= – sin (1,5T)+5cos(0,75T)

sin(1.5T)+5cos(0.75T)=5 – sin(1.5T)+5cos(0.75T)=5

Duke e shtuar atë, marrim:

10cos(0.75T)=10

2π n, n € Z

Le të zgjedhim numrin më të vogël pozitiv nga të gjithë numrat "të dyshimtë" për periudhën dhe të kontrollojmë nëse është një pikë për f. Ky numër

f(x+)=sin(1.5x+4π)+5cos(0.75x+2π)= sin(1.5x)+5cos(0.75x)=f(x)

Kjo do të thotë se kjo është periudha kryesore e funksionit f.

Problemi 4. Le të kontrollojmë nëse funksioni f(x)=sin(x) është periodik

Le të jetë T periudha e funksionit f. Pastaj për çdo x

mëkat|x+Т|=mëkat|x|

Nëse x=0, atëherë mëkat|Т|=mëkat0, mëkat|Т|=0 Т=π n, n € Z.

Le të supozojmë. Se për disa n numri π n është perioda

funksioni në shqyrtim π n>0. Pastaj sin|π n+x|=sin|x|

Kjo nënkupton që n duhet të jetë edhe një numër çift edhe një numër tek, por kjo është e pamundur. Prandaj, ky funksion nuk është periodik.

Detyra 5. Kontrolloni nëse funksioni është periodik

f(x)=

Le të jetë T periudha e f, atëherë

, pra sinT=0, Т=π n, n € Z. Le të supozojmë se për disa n numri π n është me të vërtetë periudha e këtij funksioni. Atëherë numri 2π n do të jetë periudha

Meqenëse numëruesit janë të barabartë, atëherë emëruesit e tyre janë të barabartë

Kjo do të thotë se funksioni f nuk është periodik.

Puna në grupe.

Detyrat për grupin 1.

Detyrat për grupin 2.

Kontrolloni nëse funksioni f është periodik dhe gjeni periudhën e tij themelore (nëse ekziston).

f(x)=cos(2x)+2sin(2x)

Detyrat për grupin 3.

Në fund të punës së tyre, grupet prezantojnë zgjidhjet e tyre.

VI. Duke përmbledhur mësimin.

Reflektimi.

Mësuesi u jep nxënësve karta me vizatime dhe u kërkon të ngjyrosin një pjesë të vizatimit të parë në përputhje me masën në të cilën ata mendojnë se i kanë zotëruar metodat e studimit të një funksioni për periodicitet, dhe në një pjesë të vizatimit të dytë - në përputhje me kontribut në punën në mësim.

VII. Detyre shtepie

1). Kontrolloni nëse funksioni f është periodik dhe gjeni periudhën e tij themelore (nëse ekziston)

b). f(x)=x 2 -2x+4

c). f(x)=2tg (3x+5)

2). Funksioni y=f(x) ka një periudhë T=2 dhe f(x)=x 2 +2x për x € [-2; 0]. Gjeni vlerën e shprehjes -2f(-3)-4f(3.5)

letërsi/

1. Mordkovich A.G. Algjebra dhe fillimet e analizës me studim të thelluar.
2. Matematika. Përgatitja për Provimin e Unifikuar të Shtetit. Ed. Lysenko F.F., Kulabukhova S.Yu.
3. Sheremetyeva T.G. , Tarasova E.A. Algjebra dhe fillimi i analizës për klasat 10-11.

>> Periodiciteti i funksioneve y = sin x, y = cos x

§ 11. Periodiciteti i funksioneve y = sin x, y = cos x

Në paragrafët e mëparshëm kemi përdorur shtatë veti funksione: fusha e përkufizimit, çift ose tek, monotoniteti, kufiri, vlerat më të mëdha dhe më të vogla, vazhdimësia, diapazoni i vlerave të një funksioni. Ne i përdorëm këto veti ose për të ndërtuar një grafik të një funksioni (kjo ndodhi, për shembull, në § 9), ose për të lexuar grafikun e ndërtuar (kjo ndodhi, për shembull, në § 10). Tani ka ardhur momenti i përshtatshëm për të prezantuar një veçori (të tetën) të funksioneve, e cila duket qartë në konstruksionet e mësipërme. grafikët funksionet y = sin x (shih Fig. 37), y = cos x (shih Fig. 41).

Përkufizimi. Një funksion quhet periodik nëse ka një numër T jozero të tillë që për çdo x në bashkësi vlen kushti i dyfishtë: barazisë:

Numri T që plotëson kushtin e specifikuar quhet perioda e funksionit y = f(x).
Nga kjo rrjedh se, pasi për çdo x barazimet janë të vlefshme:

atëherë funksionet y = sin x, y = cos x janë periodike dhe numri është 2 P shërben si periudhë për të dy funksionet.
Periodiciteti i një funksioni është vetia e tetë e premtuar e funksioneve.

Tani shikoni grafikun e funksionit y = sin x (Fig. 37). Për të ndërtuar një valë sinus, mjafton të vizatojmë njërën nga valët e saj (në një segment dhe më pas ta zhvendosim këtë valë përgjatë boshtit x me. Si rezultat, duke përdorur një valë do të ndërtojmë të gjithë grafikun.

Le të shohim nga i njëjti këndvështrim grafikun e funksionit y = cos x (Fig. 41). Shohim që këtu, për të vizatuar një grafik, mjafton që së pari të vizatoni një valë (për shembull, në segment

Dhe pastaj zhvendoseni atë përgjatë boshtit x nga
Duke përmbledhur, nxjerrim përfundimin e mëposhtëm.

Nëse funksioni y = f(x) ka një periudhë T, atëherë për të ndërtuar një grafik të funksionit, fillimisht duhet të ndërtoni një degë (valë, pjesë) të grafikut në çdo interval me gjatësi T (më së shpeshti merrni një interval me skajet në pika dhe më pas zhvendoseni këtë degë përgjatë boshtit x djathtas dhe majtas në T, 2T, ZT, etj.
Një funksion periodik ka pafundësisht shumë perioda: nëse T është një periudhë, atëherë 2T është një periudhë, dhe ZT është një periudhë, dhe -T është një periudhë; Në përgjithësi, një periodë është çdo numër i formës KT, ku k = ±1, ±2, ± 3... Zakonisht ata përpiqen, nëse është e mundur, të izolojnë periodën më të vogël pozitive; ajo quhet perioda kryesore.
Pra, çdo numër i formës 2pk, ku k = ±1, ± 2, ± 3, është periudha e funksioneve y = sinn x, y = cos x; 2n është periudha kryesore e të dy funksioneve.

Shembull. Gjeni periudhën kryesore të funksionit:

A) Le të jetë T periudha kryesore e funksionit y = sin x. Le të vendosim

Që numri T të jetë një periudhë e një funksioni, identiteti Por, duke qenë se po flasim për gjetjen e periudhës kryesore, marrim
b) Le të jetë T periudha kryesore e funksionit y = cos 0,5x. Le të vendosim f(x)=cos 0,5x. Atëherë f(x + T)=cos 0.5(x + T)=cos (0.5x + 0.5T).

Që numri T të jetë një periudhë e funksionit, identiteti cos (0.5x + 0.5T) = cos 0.5x duhet të jetë i qëndrueshëm.

Kjo do të thotë 0.5t = 2pp. Por, meqenëse po flasim për gjetjen e periudhës kryesore, marrim 0.5T = 2 l, T = 4 l.

Përgjithësimi i rezultateve të marra në shembull është pohimi i mëposhtëm: periudha kryesore e funksionit

A.G. Mordkovich Algjebra klasa e 10-të

Përmbajtja e mësimit shënimet e mësimit mbështetja e prezantimit të mësimit në kuadër të metodave të përshpejtimit teknologjitë interaktive Praktikoni detyra dhe ushtrime punëtori për vetëtestim, trajnime, raste, kërkime pyetje diskutimi për detyra shtëpie pyetje retorike nga nxënësit Ilustrime audio, videoklipe dhe multimedia fotografi, foto, grafika, tabela, diagrame, humor, anekdota, shaka, komike, shëmbëlltyra, thënie, fjalëkryqe, citate Shtesa abstrakte artikuj truke për krevat kureshtarë tekste mësimore fjalor termash bazë dhe plotësues të tjera Përmirësimi i teksteve dhe mësimevekorrigjimi i gabimeve në tekstin shkollor përditësimi i një fragmenti në një tekst shkollor, elemente të inovacionit në mësim, zëvendësimi i njohurive të vjetruara me të reja Vetëm për mësuesit leksione perfekte plani kalendar për vitin, rekomandimet metodologjike, programet e diskutimit Mësime të integruara