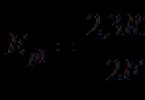Transkripsiya

1 ROSSIYA FEDERASİYASI TA'LIM VA FAN VAZIRLIGI "Togliatti davlat universiteti" Federal davlat byudjetli oliy ta'lim muassasasi Matematika, fizika va axborot texnologiyalari instituti "Algebra va geometriya" kafedrasi "MAVZU BO'YICHA Talabalarga o'qitish metodikasi" BASOSSIY MAKTAB ALGEBRA KURS B AKA L A V R S K A Y ISH Bakalavriat tayyorlash yo nalishi: Pedagogik ta lim Yo nalish (profil): Matematika va informatika Talaba V.V. Nazarov Ilmiy rahbar: pedagogika fanlari doktori, prof. R.A. Uteeva Himoyaga qabul qilinadi Kafedra mudiri: pedagogika fanlari doktori, prof. R.A. Uteeva 016 Tolyatti - 016

2 MUNDARIJA KIRISH... I bob. BAYOSIB MAKTAB ALGEBRA KURSDA “Kvadrat ildizlar” MAVZUSINI O‘QITISHNING METODOLIK TIZIMI. Tayanch maktab algebra kursi maktablarida “Kvadrat ildizlar” mavzusi Tayanch maktab algebra kursida “Kvadrat ildizlar” mavzusini o‘qitish shakllari, usullari va vositalari... 5 I bob bo‘yicha xulosa... II BOB. MAKTAB ALGEBRA KURSDA “Kvadrat ildizlar” MAVZUSINI O‘QITISHNI TASHKIL BO‘YICHA METODIK TAVSIYALAR “Kvadrat ildizlar” mavzusidagi topshiriqlar, maktab algebra fanidan boshlang‘ich bilim va ko‘nikmalarga yo‘naltirilgan “Ildiz” mavzusi bo‘yicha topshiriqlar. yakuniy attestatsiyaga tayyorgarlik ko'rish va matematika bo'yicha OGE ni topshirishga qaratilgan II bob bo'yicha xulosa.

3 KIRISh Tadqiqotning dolzarbligi. "Kvadrat ildizlar" mavzusi asosiy maktab algebra kursining an'anaviy mavzularidan biridir. Uning olingan raqamlarni o'rganishi 6-sinfning ratsional matematika kursi bo'yicha o'quvchilarning bilim va ko'nikmalariga asoslangan. Ratsional sonlar ustida amallarni bajarish malakalarini oshirish 7-sinf algebra kursida uchraydi. 8-sinf algebra kursida “Kvadrat ildizlar” mavzusini o’rganishning ahamiyati va o’rni ratsional sonlar to’plamini yanada kengaytirish va irratsional sonlarni kiritish zarurati bilan bog’liq. Mavzuni o'rganish uchun motivatsiya kvadratning berilgan maydoniga asoslangan tomonini (yon uzunligini) topishning mashhur amaliy muammosi bo'lishi mumkin, uni hal qilish uchun avval ma'lum bo'lgan raqamlar etarli emas. Bundan tashqari, ko'plab geometrik masalalar, fizika, kimyo va biologiyaga oid masalalarni yechishda kvadrat ildizlari bo'lgan tenglamalarni echish kerak bo'ladi. Shuning uchun kvadrat ildizlar bilan amallar qoidalarini bilish va ularni o'z ichiga olgan ifodalarni o'zgartirishni o'rganish muhimdir. Keling, quyidagi manbalar asosida tuzilgan kvadrat ildiz tushunchasining kelib chiqish tarixi va uning belgilanishiga murojaat qilaylik. n X va x kvadrat ildiz belgisining zamonaviy shakli darhol paydo bo'lmagan. Radikal belgining evolyutsiyasi deyarli besh asr davom etdi, 13-asrdan boshlab, italyan va ba'zi evropalik matematiklar birinchi marta 15-asrda lotincha Radix (ildiz) so'zi yoki qisqartirilgan R. bilan kvadrat ildiz deb atashgan. N. Shuke 1 oʻrniga R 1 ni yozgan. Zamonaviy ildiz belgisi 15—16-asrlar nemis matematiklari tomonidan qoʻllanilgan belgidan kelib chiqqan boʻlib, ular algebra fanini “Koss”, algebra matematiklari esa “Kossistlar” deb atashgan. (12—15-asrlar matematiklari barcha asarlarini faqat lotin tilida yozganlar. Ular nomaʼlum res (narsa) deb atashgan).

4 italyan matematigi res so'zini kosa deb tarjima qilgan. Oxirgi atama nemislar tomonidan qarzga olingan, ulardan kossistlar va kosslar paydo bo'lgan.) 15-asrda. Ba'zi nemis kossistlari kvadrat ildizni belgilash uchun ifoda yoki raqamdan oldin nuqta qo'yishgan. Kursiv yozuvda bu nuqtalar tire bilan almashtirilgan, keyinchalik ular timsolga aylangan.Bunday belgilardan biri oddiy kvadrat ildizni bildirgan. Agar to'rtinchi darajali ildizni ko'rsatish kerak bo'lsa, u holda ikkilamchi belgi ishlatilgan. Sakkizinchi ildiz qanday aniqlanganligini faqat taxmin qilish mumkin. Agar biz to'rtinchi daraja bilan o'xshashlikni oladigan bo'lsak, unda bu belgi kvadrat ildizning uch karrali ekstraktsiyasini aniqlashi kerak edi, ya'ni buning uchun uchta kvadrat qo'yish kerak edi. Biroq, bu belgi kub ildizi bilan band. Ehtimol, aynan shunday belgilardan V belgisi keyinchalik shakllangan bo'lib, u yozma ravishda maktab o'quvchilariga tanish bo'lgan zamonaviy belgiga yaqin, ammo yuqori chiziqsiz. Bu belgi birinchi marta nemis algebrasida "Algebraning mahoratli qoidalari yordamida chiroyli va tez hisoblash" da ko'rilgan. Ushbu ishning muallifi venalik matematika o'qituvchisi, Chexiya Respublikasida tug'ilgan Kristof Rudolf edi. Kitob katta muvaffaqiyatlarga erishdi va 16-asr davomida doimiy ravishda qayta nashr etildi. va 1615 yilgacha. Krishtof taklif etgan ildiz belgisini A.Jirard, S.Stevinlar qoʻllagan (u ildiz koʻrsatkichini aylana boʻylab radikal belgining oʻng tomoniga yozgan: V () yoki V (). 166 yilda golland matematigi A. .Jirard Rudolf ildizining belgisini oʻzgartirib, zamonaviy yozuvga juda yaqin boʻlganini kiritdi.Bu yozuv shakli oldingi R belgisini siqib chiqara boshladi.Lekin bir muncha vaqt ildiz belgisi yuqori chiziqni sindirish yoʻli bilan yozildi, yaʼni shunday. : a + b. Va faqat 167 yilda Rene Dekart o'zining "Geometriya" kitobida yangi belgidan foydalanib, gorizontal chiziqni tasdiq belgisi bilan bog'ladi. Lekin bu erda ham zamonaviy shaklning aniq nusxasi yo'q edi. Dekartning rekordi biroz boshqacha edi. Biz o‘rganib qolganimizdan bir tafsilotga.Uning 4 tasi bor

5 yozildi: C + 1 q qq p, bu erda radikaldan keyin darhol qo'yilgan C harfi kub ildiz belgisini ko'rsatdi. Zamonaviy ko'rinishda bu ifoda quyidagicha ko'rinadi: C + 1 q q p. Radikalning zamonaviy yozilishiga eng yaqin narsa Nyuton tomonidan "Universal arifmetika" (1685) asarida ishlatilgan.Ildizning bugungi kunga to'liq mos keladigan birinchi yozuvi frantsuz matematigi Rolning "Manual of" kitobida topilgan. Algebra”, 1690 yilda nashr etilgan. U yozilganidan bir muncha vaqt o'tgach, sayyora matematiklari nihoyat kvadrat ildiz uchun yozuvning yagona va yakuniy shaklini qabul qilishdi. Tadqiqot muammosi: maktabda "Kvadrat ildizlar" mavzusini o'qitishning uslubiy xususiyatlari qanday? 8-sinf algebra kursida 5, tayanch O`quv ob`ekti boshlang`ich sinf o`quvchilariga algebra fanini o`rgatish jarayonidir. Tadqiqot predmeti “Kvadrat ildizlar” mavzusini o‘qitishning metodik tizimidir. Bakalavrlik dissertatsiyaning maqsadi “Kvadrat ildizlar” mavzusini o‘qitishning metodik tizimini ochib berishdan iborat. Tadqiqot vazifalari: 1. Tayanch maktab algebra kursida “Kvadrat ildizlar” mavzusini o‘qitishning asosiy maqsad va vazifalarini aniqlash (metodik tizimning maqsadli komponenti).. “Kvadrat ildizlar” mavzusi mazmunini tahlil qilish. tayanch maktabning algebra darsliklarida (metodik tizimning mazmun komponenti).. Tayanch maktab (tashkiliy) algebra kursida “Kvadrat ildizlar” mavzusini o‘qitishning turli shakllari, usullari va vositalarini o‘rganish.

uslubiy tizimning 6 komponenti). 4. “Kvadrat ildizlar” mavzusini o‘qitish bo‘yicha uslubiy tavsiyalarni shakllantirish. Tadqiqot usullari: tadqiqot mavzusi bo'yicha ilmiy-uslubiy adabiyotlar, matematika dasturlari, maktab algebra darsliklarini tahlil qilish, materialni tahlil qilish, tizimlashtirish va umumlashtirish. Ushbu ishning amaliy ahamiyati shundan iboratki, unda maktab algebrasining asosiy kursida “Kvadrat ildizlar” mavzusini o‘qitishning uslubiy tizimi taqdim etilgan va matematika o‘qituvchilari, shuningdek bakalavrlar tomonidan o‘quv amaliyotida qo‘llanilishi mumkin bo‘lgan uslubiy tavsiyalar ishlab chiqilgan. maktab. Bakalavr ishining taqdim etilgan natijalari va xulosalari talabalarga "Kvadrat ildizlar" mavzusini o'qitish usullarini yanada rivojlantirish uchun asos bo'lishi mumkin. Himoyaga taqdim etilgan: asosiy maktab algebrasi kursida "Kvadrat ildizlar" mavzusini o'qitishning uslubiy tizimi. Ish tuzilishi. Bakalavriat ishi kirish, ikki bob, xulosa va foydalanilgan adabiyotlar ro‘yxatidan iborat. 6

7 I-BOB. ASOSIY MAKTAB ALGEBRA KURSIDA “Kvadrat ildizlar” MAVZUSINI O‘QITISHNING USLUBIY TIZIMI 1. Tayanch maktab algebrasi kursida “Kvadrat ildizlar” mavzusini o‘qitishning asosiy maqsad va vazifalari Federal davlat umumiy ta’lim standartida. Ta'lim (FSES MChJ) ta'kidlanishicha, "Matematika" o'rganiladigan fan yo'nalishi quyidagilarni ta'minlashi kerak: 1) real jarayon va hodisalarni tasvirlash va o'rganish imkonini beradigan haqiqatni tushunish usuli sifatida matematika haqidagi g'oyalarni shakllantirish;) ko'nikmalarni rivojlantirish. o'quv matematik matn bilan ishlash (tahlil qilish, kerakli ma'lumotlarni ajratib olish), matematik terminologiya va simvolizmdan foydalangan holda o'z fikrini to'g'ri va malakali ifodalash, matematik bayonotlarni tasniflash, mantiqiy asoslash, isbotlash; haqiqiy raqamlarga; og'zaki, yozma, instrumental hisoblash ko'nikmalarini egallash; 4) algebraning ramziy tilini, ifodalarni bir xil o‘zgartirishlarni bajarish, tenglamalar, tenglamalar, tengsizliklar va tengsizliklar sistemalarini yechish usullarini egallash; real vaziyatlarni algebra tilida modellash, algebra yordamida tuzilgan modellarni tekshirish va olingan natijalarni sharhlash qobiliyati; Matematika dasturida muallif “Kvadrat ildizlar” mavzusini o‘rganish bo‘yicha quyidagi maqsad va vazifalarni belgilaydi: Ratsional sonlar to‘plamini kengaytirish, irratsional va haqiqiy sonlar tushunchasini kiritish, kvadrat ildizlar va ular bilan amallarni o‘rganish. 7

8 Mavzuni o‘rganish natijasida talabalar bilishlari kerak: 1. Davriy va davriy bo‘lmagan cheksiz o‘nli kasrlarning ta’rifi.. y=x funksiya, uning xossalari va grafigi.. Kvadrat ildiz haqida tushuncha 4. Arifmetikaning xossalari. kvadrat ildizlar. 5. Haqiqiy, ratsional va irratsional sonlar to`plami. Mavzuni o`rganish natijasida talabalar: 1. Oddiy kasrni o`nli kasrga va aksincha o`tkazishni.. Haqiqiy, ratsional va irratsional sonlarni solishtira olish.. y=x funksiya grafigini tuza olish. 4. Ildiz belgisi ostidan multiplikatorni qo'shing va olib tashlang. 5. Kvadrat ildizlar bilan amallarni bajaring. Matematika dasturida muallif "Kvadrat ildizlar" mavzusini o'rganish uchun quyidagi maqsad va vazifalarni belgilaydi (Makarychevning darsligi uchun): Ratsional sonlar haqidagi ma'lumotlarni tizimlashtirish va irratsional sonlar haqida tushuncha berish, shu bilan son tushunchasini kengaytirish; kvadrat ildizlarni o'z ichiga olgan ifodalarni oddiy o'zgartirishni amalga oshirish qobiliyatini rivojlantirish. Mavzuni o`rganish natijasida talabalar bilishlari kerak: 1. Natural, butun, ratsional, irratsional va haqiqiy sonlar.. A sonining moduli.. Arifmetik kvadrat ildiz va uning xossalari. 4. y= x funksiya, uning xossalari va grafigi. Mavzuni o`rganish natijasida talabalar: 1. Eng oddiy kvadrat tenglamalarni yecha olishlari kerak. 8

9 . Ildiz belgisi ostidagi ko'paytirgichni qo'shing va olib tashlang. Kvadrat ildizlarning taxminiy qiymatlarini toping. 4. Sonning kuchining kvadrat ildizini oling. 5. Irratsional ifodalarni o‘zgartiring. Matematika dasturida muallif Alimov darsligidagi “Kvadrat ildizlar” mavzusini o‘rganish bo‘yicha quyidagi maqsad va vazifalarni belgilab beradi: Ratsional sonlar haqidagi ma’lumotlarni tizimlashtirish va irratsional sonlar haqida tushuncha berish, shu orqali son tushunchasini kengaytirish; kvadrat ildizlarni o'z ichiga olgan ifodalarni oddiy o'zgartirishni amalga oshirish qobiliyatini rivojlantirish. Mavzuni o`rganish natijasida talabalar bilishlari kerak: 1. Arifmetik kvadrat ildiz tushunchasi.. Haqiqiy sonlar Mavzuni o`rganish natijasida o`quvchilar daraja, ko`paytma va kasrning kvadrat ildizini topa olishlari kerak. S.Minaeva [, 4-7-betlar] maqolasida “Kvadrat ildizlar” bo‘limini o‘rganish quyidagi maqsadlarni ko‘zda tutilishi qayd etilgan: tarkibida kvadrat ildizlar bo‘lgan ifodalarni o‘zgartirishni amalga oshirishni o‘rgatish; Kvadrat va kub ildizlar misolidan foydalanib, n- ildiz haqida boshlang'ich g'oyalarni shakllantiring. 015 yil 8 apreldagi asosiy umumiy ta'limning taxminiy asosiy ta'lim dasturida bitiruvchi 8-sinfda o'rganishi kerak (kundalik hayotda foydalanish, boshqa fanlarni o'rganish va asosiy darajadagi ta'limni muvaffaqiyatli davom ettirish imkoniyatini ta'minlash uchun): 1. Asosiy darajada amal qiling: darajadagi tushunchalar: natural son, butun son, oddiy kasr, o‘nli kasr, aralash kasr, ratsional son, arifmetik kvadrat ildiz.. Musbat butun sonning kvadrat ildizining qiymatini hisoblang. 9

10 . Ratsional va irratsional sonlarni bilish. 4. Raqamlarni solishtiring. 5. Sonni standart shaklda yozish ma’nosini tushuning. 6. Kvadrat tenglamaning ildizlari formulasidan foydalanib, kvadrat tenglamalarni yeching. 7. Tengsizliklar va ularning sistemalarini sanoq chizig‘ida yechimini chizing. Bitiruvchi 8-sinfda asosiy va yuqori darajalarda ta’limni muvaffaqiyatli davom ettirish imkoniyatini ta’minlash uchun quyidagilarni o‘rganish imkoniyatiga ega bo‘ladi: 1. Tushunchalar bilan amal qiling: natural sonlar to‘plami, butun sonlar to‘plami, ratsional sonlar to‘plami, irratsional son, kvadrat. ildiz, haqiqiy sonlar to‘plami, natural sonlarning geometrik talqini, butun sonlar, ratsional, haqiqiy sonlar.. Hisoblash ishlarini, shu jumladan ratsional hisoblash texnikasidan foydalangan holda.. Ratsional va irratsional sonlarni solishtiring. 4. Ratsional sonni o‘nli kasr shaklida ifodalang. 5. Kvadrat ildizlari bo'lgan ifodalarni o'zgartirishni bajaring. 6. Kvadrat ildizli iboralarda binom yig‘indisi yoki ayirmasining kvadratini aniqlang.. Tayanch maktab algebrasi kursida “Kvadrat ildizlar” mavzusini o‘qitish mazmunini uslubiy tahlil qilish. algebra 7-sinf) bilimlar: ratsional son tushunchasi; ratsional sonlar to‘plami haqida tushuncha va uning belgilanishi; 10 va kurs

Ratsional sonlar bilan 11 ta asosiy harakat (operatsiya); y = x funktsiyasi. Yangi (kiritilgan) bilimlar: sonning kvadrat ildizi tushunchasi; arifmetik kvadrat ildiz haqida tushuncha; arifmetik kvadrat ildizlarning xossalari; ildiz belgisi ostidagi ko‘paytuvchini qo‘shish va ayirish; kvadrat ildizlar bilan amallar. 8-sinf algebra fanidan turli darsliklardagi “Kvadrat ildizlar” mavzusining mazmuni tahlili 1-4-jadvallarda keltirilgan. Darslikda Yu.N. Makarycheva "Kvadrat ildizlar" bo'limini o'rganish uchun boshqa soatlarga qaraganda ko'proq soat ajratadi, butun bo'lim 4 paragrafga bo'lingan. Kvadrat ildizlarni taxminiy aniqlashni o'rganish mavzusi ko'rib chiqiladi, lekin davriy o'nli kasrlar mavzusi o'tkazib yuboriladi. Darslikda G.K. Muravin va O.V. Muravina "Kvadrat ildizlar" bo'limiga 18 soatdan ozroq vaqt ajratdi, bo'lim paragraflardan iborat, davriy o'nli kasrlar mavzusi ko'rib chiqiladi, ammo kvadrat ildizlarning taxminiy topilmasi yo'q. Nikolskiyning darsligida "Kvadrat ildizlar" bo'limi faqat bitta paragraf va 5 banddan iborat bo'lib, ko'plab mavzular va tushunchalar taqdim etilmaydi. Darslikda G.V. Dorofeev Pifagor teoremasiga bag'ishlangan mavzuni o'z ichiga oladi, bu yuqorida aytilganlarning barchasida mavjud emas. Bu erda kub ildizlarini o'rganishga ham to'xtalib o'tadi. Barcha darsliklarda bo'limni o'rganish haqiqiy va irratsional sonlardan boshlanadi, ammo har bir muallifning o'ziga xos yondashuvi bor. Keyin kvadrat ildizning o'zi va arifmetik kvadrat ildiz, xossalari va ular ustida amallarni o'rganish keladi. o'n bir

12 Darslik mualliflari Yu.N. Makarychev, N.G. Mindyuk, K.I. Neshkov, S.B. Suvorova Bob va paragraflar sarlavhalari 4. Haqiqiy sonlar 9. Ratsional sonlar 10. Irratsional sonlar 5. Arifmetik kvadrat ildiz 11. Kvadrat ildizlar. Arifmetik kvadrat ildiz. 1. Tenglama x =a. 1. Kvadrat ildizning taxminiy qiymatlarini topish. 14. y= x funksiya va uning grafigi. 6. Arifmetik kvadrat ildizning xossalari. 15. Ko‘paytma va kasrning kvadrat ildizi. 16. Darajaning kvadrat ildizi. 7. Arifmetik kvadrat ildiz xossalarini qo'llash 17. Ildiz belgisi ostidagi omilni olib tashlash. Ildiz belgisi ostida ko'paytirgichni kiritish. 18. Kvadrat ildizlari bo'lgan ifodalarni o'zgartirish. 1-jadval Soatlar soni Jami Jadval Darslik mualliflari G.K. Muravin, K.S. Muravin, O.V. Muravina Bob va paragraflar sarlavhalari 5. Haqiqiy sonlar 14. Ratsional va irratsional sonlar. 15. Davriy va davriy bo'lmagan cheksiz o'nli kasrlar. 6. Kvadrat ildizlar. 16. y=x funksiya va uning grafigi. 17. Kvadrat ildiz haqida tushuncha. 18. Arifmetik kvadrat ildizlarning xossalari. 19. Ko‘paytuvchini ildiz belgisi ostidan qo‘shish va ayirish. 0. Kvadrat ildizli amallar. Soatlar soni Jami 18 Jadval Darslik mualliflari S.M. Nikolskiy, M.K. Potapov, N.N. Reshetnikov, A.V. Shevkin Boblar va paragraflar sarlavhalari. Kvadrat ildizlar.1 Kvadrat ildiz haqida tushuncha.. Arifmetik kvadrat ildiz.. Natural sonning kvadrat ildizi..4 Kvadrat ildizlarning taqribiy hisobi..5 Arifmetik kvadrat ildizlarning xossalari. 1

13 4-jadval Darslik mualliflari Boblar va paragraflar nomi Soatlar soni G.V. Dorofeev .1 Kvadrat tomonini topish masalasi. Irratsional sonlar. Pifagor teoremasi.4 Kvadrat ildiz (algebraik yondashuv).5 Kvadrat ildizlarning xossalari.6 Kvadrat ildizlari bo‘lgan ifodalarni o‘zgartirish.7 Kub ildiz Jami 18 “Kvadrat ildizlar” mavzusini 8-sinf uchun algebra darsligi asosida mualliflar Muravin tomonidan o‘rganish. . Boshida ratsional sonlar to‘plamining kengayishi keltiriladi, irratsional va haqiqiy sonlar tushunchalari kiritiladi, oddiy kasrlardan o‘nli kasrlarga va aksincha o‘tish ko‘rib chiqiladi. Ratsional va irratsional sonlarga bir soat vaqt ajratiladi.14-bandda “Ratsional va irratsional sonlar” ularning paydo bo’lish tarixi va mavzuni o’rganishdan maqsadi haqida so’z boradi. Ta'riflar misollar va segment uzunliklarining nisbatlari asosida berilgan. 1-ta'rif: agar ikkita bo'lakning bir segmentida m marta va ikkinchisida n marta to'g'ri keladigan umumiy o'lchovi bo'lsa, ularning nisbati m, n ratsional sondir. Irratsional sonning ta'rifi 1-misolda keltirilgan: 1-misol: d = (m n) =. Demak (m n) =. Tenglamaning chap tomonidagi kasrning maxraji bittadan farq qiladi, shuning uchun kasr butun songa teng bo'lishi uchun uni n ga kamaytirish kerak. Lekin m va n natural sonlarining umumiy bo‘luvchilari yo‘q, shuning uchun ularning kvadratlarida ham umumiy bo‘luvchilar yo‘q. Bu m = tengligi noto'g'ri ekanligini anglatadi, ya'ni. d soni kasr emas. n 1

14 Misol d sonining ratsional son emasligini isbotladi, demak, kvadratning diagonali uning tomoni bilan umumiy o'lchovga ega emas, d soni irratsional sondir. Keyingi paragraf davriy va davriy bo'lmagan kasrlarga bag'ishlangan bo'lib, davr tushunchasi kiritiladi va tarjima paytida davr paydo bo'lishining muqarrarligi asoslanadi. Ushbu bandga bir soat vaqt ajratilgan.15-bandda davriy va davriy bo'lmagan o'nli kasrlar o'rganilib, ratsional va irratsional sonlarning ildizini taqribiy aniqlash mavzusi ko'rib chiqiladi. Keyin ko'rib chiqilgan misollardan foydalanib, chekli va cheksiz o'nli kasrlarga ta'riflar beriladi. Misol: 1 ni o'nli kasrga aylantiramiz, shunday bo'ladi: 0. Yozuvda cheksiz takrorlanadigan songa nuqta, kasrning o'zi esa davriy deyiladi. 1-xususiyat: har qanday ratsional sonni cheksiz davriy o'nli kasr sifatida ko'rsatish mumkin (buning aksi ham to'g'ri). Ta'rif: Har qanday irratsional son cheksiz davriy bo'lmagan o'nli kasr sifatida yoziladi va har qanday cheksiz davriy bo'lmagan o'nli kasr irratsional sondir. Ta'rif: Cheksiz davriy o'nli kasr ratsional son, cheksiz davriy bo'lmagan o'nli kasr esa irratsional sondir. Shundan so'ng to'g'ridan-to'g'ri "Kvadrat ildizlar" mavzusini o'rganishga o'tiladi. Tadqiqot “y=x funksiya va uning grafigi” bandi bilan boshlanadi. Funktsiyalar va grafiklar bo'yicha materiallar takrorlanadi. Bir soat ajratiladi.Dastavval dekart koordinata sistemasidagi nuqtalarda y=x funksiyaning grafigi tuziladi, uni o’rganish amalga oshiriladi va grafik nomi beriladi: 4-ta’rif: y=x funksiya grafigi. parabola deyiladi. 14

15 Kvadrat ildiz tushunchasiga o'tish kvadrat tenglamani x =a yechish orqali sodir bo'ladi, bunday usul atamaning mohiyatini tushuntirishga imkon beradi, deb ta'kidlaydi. Soatlar ajratilgan.Keyingi 17-bandda kvadrat ildiz tushunchasi kiritilgan. 5-ta’rif: x =a tenglamaning ildizlari a ning kvadrat ildizlari deyiladi. 6-ta’rif: Kvadrati a ga teng bo‘lgan manfiy bo‘lmagan son a ning arifmetik kvadrat ildizi deyiladi va a bilan belgilanadi. . Radikal belgisi kiritiladi va uning kelib chiqish tarixi keltiriladi. Keyin mualliflar arifmetik kvadrat ildizlarning xossalarini o'rganishga o'tadilar, bu vaqtda ular kvadrat ildizli ifodalarni o'zgartirish qobiliyatini rivojlantira boshlaydilar. Qism berilgan.18-bandda arifmetik kvadrat ildizlarning xossalari berilgan: Xoslik: Har qanday a a = a soni uchun. Xossa: a va b manfiy bo'lmagan har qanday sonlar uchun: ab= a b . Shundan so‘ng, ko‘paytuvchini ildiz belgisi ostidan qo‘shish va ayirish mavzusi o‘rganiladi va mashq qilinadi. Ish kvadrat ildizlar bilan davom etadi. Mualliflar ta'kidlaganidek, o'quvchilar to'g'ridan-to'g'ri iboralarni o'zgartirishda qiyinchiliklarga duch kelishlari mumkin, chunki bu vaziyatda ko'paytirgichni ildiz belgisi ostidan olib tashlashda modul belgisi muhim ahamiyatga ega. Qism berilgan.19-bandda ko‘paytuvchining ildiz belgisining rejimlaridan kiritilishi va olib tashlanishi o‘rganilib, xossasi berilgan: 4-xususiyat: manfiy bo‘lmagan qiymatlar uchun b a b= a * b= a * b. Keyinchalik, mualliflar kvadrat ildizlar bilan operatsiyalarga o'tadilar, bu vaqtda asosan raqamli ifodalarni o'zgartirishda mashq qiladilar, 15

16 nafar maktab o‘quvchisi ushbu mavzu bo‘yicha bilimlarini chuqurlashtirmoqda. O'rganishni ikki qismga bo'lish mumkin: 1. Sonlarning kvadrat ildizlari bilan ishlash.. Harfiy ifodalarni o'zgartirish. Ushbu o'rganish modeli o'rganish ketma-ketligini belgilamaydi, aytishimiz mumkinki, ikkinchi qism, garchi bu bosqichda foydali bo'lsa ham, 9-sinf materialining propedevtikasini amalga oshiradi, bu erda harfli ifodalarni radikallar bilan o'zgartirish maxsus o'rganiladi. 4 soat ajratilgan. 0-bo'limda va oxirgi bo'limda biz kvadrat ildizlar bilan amallarni o'rganamiz. Ular ilgari o'rganilgan xususiyatlarni eslaydilar va ulardan raqamli ifodalarni o'zgartirish uchun foydalanadilar. maxrajdagi irratsionallikdan ozod qilish, faktorlashtirish, ifodani soddalashtirish kabi harakatlar ko'rib chiqiladi. Jami bo‘limni o‘rganish uchun mualliflar 19 soat vaqt ajratadilar, har bir bo‘limdan keyin test yoki mustaqil ish, bob oxirida esa test topshiriladi. Yu.N.ning 8-sinf uchun algebra darsligi asosida “Kvadrat ildizlar” mavzusini o'rganish. Makarycheva. "Kvadrat ildizlar" bobi haqiqiy sonlarni ko'rib chiqish bilan boshlanadi. Birinchidan, natural sonlar to‘plami, natural sonlarning bo‘linuvchanligi haqidagi asosiy ma’lumotlar eslatiladi va mavzu bo‘yicha tipik masalalarni ko‘rib chiqish. Soatlar ajratiladi.Soʻngra butun sonlar haqidagi asosiy maʼlumotlarni koʻrib chiqish va tipik masalalarni koʻrib chiqish uchun bitta dars, soʻngra ratsional sonlar toʻplamiga bagʻishlangan dars. Keyinchalik irratsional sonlar va haqiqiy sonlar to'plami tushunchasi bilan tanishadigan dars. Yuqorida aytib o'tilgan darslardan so'ng, 16-chi boshlanadi

17 kvadrat ildizlarni to'g'ridan-to'g'ri o'rganish, kvadrat ildiz va arifmetik kvadrat ildiz tushunchalari muhokama qilinadigan dars. Keyin dars eng oddiy kvadrat tenglamalarni yechishga bag'ishlangan x =a va keyin kvadrat ildizlarning taxminiy qiymatlarini topishni o'rganadigan 1 dars. Keyingi darsda y= x funksiya, uning xossalari va grafigiga e’tibor qaratiladi. Quyida arifmetik kvadrat ildizning xususiyatlariga oid darslar keltirilgan. 1-darsda ko‘paytma va kasrning kvadrat ildizining xossalari muhokama qilinadi, keyingi darsda sonning kvadrat ildizini qanday chiqarish mumkinligi ko‘rib chiqiladi. Ushbu bosqichda muallif testda bir nechta darslarni o'tkazish va uni tekshirishni taklif qiladi, so'ngra arifmetik kvadrat ildizning xususiyatlarini qo'llash bilan bog'liq bo'lgan darslarga o'tishni taklif qiladi. Ko‘paytuvchini ildiz belgisi ostidan qo‘shish va ayirish ko‘nikmalarini takrorlash va mashq qilish uchun 1 ta dars. Keyin irratsional ifodalarni aylantirishning asosiy usullarini o'z ichiga olgan dars. Xulosa qilib aytganda, muallif "Kvadrat ildizlar" mavzusida yakuniy test o'tkazishni taklif qiladi. Ushbu bo'limni o'rganish uchun jami bir soat vaqt ajratilgan. Endi G.V.ning darsligidan foydalanib algebra darslarida kvadrat ildiz tushunchasini kiritish bo‘yicha S.Minaevaning tavsiyalarini ko‘rib chiqamiz. Dorofeeva 8-sinfda: 1. Kvadrat tomonini topish masalasi (dars) Kvadrat ildiz tushunchasini kiritish uchun motivatsion va semantik jihatlarni ajratib ko'rsatuvchi ushbu kursga xos bo'lgan mazmunli yondashuv qo'llaniladi. Material quyidagicha taqdim etiladi: talabalar S = a formulasini bilishadi, bu formula yordamida kvadratning a tomonini ishlatib, uning S maydonini hisoblash mumkin; lekin matematikada 17 dan kvadratning tomonini topishga teskari masalani yechish formulasi mavjud.

Berilgan S maydonning 18 tasi, u quyidagicha yoziladi: a = S. S belgisi maydoni S ga teng bo‘lgan kvadratning tomonini bildiradi. Masalan, S = 100 bo‘lsa, a = 100. 100 = bo‘lgani uchun 10, keyin a = 100 = 10. Talabalar yangi belgini o'rganishlari uchun siz bir nechta savollarni taklif qilishingiz mumkin: kvadratning maydoni 81 m bo'lsin: belgidan foydalanib, yon tomoni uchun ifoda yozing. bu kvadrat; kvadrat tomonining uzunligi qancha? Geometrik tildan algebraik tilga o‘tsak, S belgisining ma’nosini quyidagicha ta’riflash mumkin: S – manfiy bo‘lmagan son, kvadrati S ga teng. (Axir, uzunlikni manfiy son sifatida ifodalab bo‘lmaydi! ) Shunday qilib, biz kvadrat ildizlarning qiymatlarini topishda foydalanadigan "ishchi" formulaga erishamiz. Biz o'qituvchining diqqatini S belgisi qanday o'qilishiga qaratamiz: S ning kvadrat ildizi. Bu erda "arifmetik" sifatdoshi ortiqcha, chunki mavzuning bu nuqtasida biz faqat ijobiy ildizlar bilan ishlaymiz. Biroq, bu atama keyinroq qo'llaniladi.. Irratsional sonlar (dars) Shu o'rinda ikki jihatni ajratib ko'rsatish mumkin: g'oyaviy va amaliy. Mafkuraviy narsa irratsional sonlar bilan birinchi tanishuvda yotadi; amaliy - "olinmaydigan" ildizlarni baholash qobiliyatini rivojlantirishda, ularning taxminiy qiymatlarini smeta va kalkulyator yordamida toping. Talabalar irratsional sonlarni kiritish zaruriyatiga kvadratning maydoniga qarab uning tomonini topishga oid allaqachon tanish bo'lgan masalani ko'rib chiqish natijasida keladi. Darslikda 10-rasmda ikkita kvadrat ko'rsatilgan. Ulardan biri bitta, uning maydoni 1 kvadrat. birliklar Ikkinchi kvadratning yon tomoni birinchisining diagonali bo'lib, uning maydoni ikki baravar katta. (Aslida kichik kvadrat ikkita teng uchburchakdan, kattasi esa to'rtta shunday 18 tadan iborat.

19 ta uchburchak mavjud.) Bu katta kvadratning maydoni sq ga teng degan ma'noni anglatadi. birliklar Bu kvadratning yon uzunligi qancha? Uni a bilan belgilaymiz. Kvadrat ildiz belgisidan foydalanib, a= deb yozishimiz mumkin. Talabalar shu paytgacha faqat "chiqarib olinadigan" ildizlar bilan shug'ullanishgan. Siz ularga bir necha daqiqa vaqt berishingiz kerak, shunda ular a = 1 qiymati etarli emasligiga ishonch hosil qilish uchun ildizni ajratib olishga harakat qilishadi va agar siz = olsangiz, u allaqachon juda ko'p; o'nlik kasrni topishga harakat qilib, 1.4<, а 1,5 >. Keyinchalik, kvadrati teng bo'lgan butun son ham, kasr ham yo'qligini juda oddiy isbotlash amalga oshiriladi (darslikning 7-bet). Shunday qilib, bizning kvadratimiz tomonining uzunligini aniq ifodalovchi ratsional son yo'q. Talabalar qadimgi matematiklar erishgan ajoyib kashfiyotni (segment bor, lekin uning uzunligi yo'q!), shuningdek, bu fakt matematikaning rivojlanishiga turtki berganligini (yangi raqamlarni kiritish kerak edi!) . O'quvchilarga kvadrat tomonining uzunligini ifodalovchi raqam aytiladi, uning maydoni kv. birliklar, irratsional sonlar deb ataladigan sinfga kiradi: - bu kvadrati teng bo'lgan musbat irratsional son, ya'ni () = tengligi to'g'ri. Ular a shaklidagi boshqa irratsional sonlarni nomlay olishlari va a ning o'ziga xos ijobiy qiymatlari uchun har ikki yo'nalishda (a) =a kabi o'zgarishlarni amalga oshirishlari kerak. Shunday qilib, irratsional sonlar bilan birinchi tanishish ancha tor maqsadga bo'ysunadi: u kvadrat ildizlarni o'rganish bilan bog'liq bo'lib, birinchi navbatda, ushbu mavzuning ehtiyojlarini ta'minlaydi. Yuqorida tavsiflangan ma'lumotlarga qo'shimcha ravishda (masalan: ratsional sonlar orasida maydoni teng bo'lgan kvadrat tomonining uzunligini ifodalovchi raqam yo'q; ratsional sonlardan tashqari, irratsional sonlar ham mavjud 19

20; irratsional sonlar a ko‘rinishidagi barcha raqamlarni o‘z ichiga oladi, agar a butun son yoki kasr sonning kvadrati bo‘lmasa), o‘quvchilar turli tabiatdagi cheksiz ko‘p irratsional sonlar mavjudligini (masalan, z soni), irratsional sonlar manfiy bo'ladi va amalda ular (taxminan) o'nli kasrlar bilan almashtiriladi. Talabalar 9-sinf kursining “ikkinchi o‘tish”ida irratsional va haqiqiy sonlar haqida to‘liqroq ma’lumot oladilar. A ko'rinishidagi irratsional sonning o'nli yaqinligini topishning asosiy imkoniyatini ko'rsatish uchun darslikda baholash usuli qo'llaniladi: kamchiliklar va ortiqcha bo'lgan taxminiy qiymatlar topiladi, ular ketma-ket butun sonlar sifatida ifodalanadi (ya'ni 1 ga aniqlik). ), bir kasrli ketma-ket o'nli kasrlar (ya'ni, 0,1 gacha aniqlik bilan) va hokazo. Ushbu usulning asosi quyidagi bayonotdir: a va b musbat sonlar va a bo'lsa.

21 To‘g‘ri burchakli uchburchak gipotenuzasi uzunligini uning oyoqlaridan hisoblash uchun Pifagor teoremasini qo‘llash munosabati bilan (84-betdagi 1-misol) darslikda “Pifagor uchliklari” haqida so‘z yuritilgan. E'tibor bering, ular cheksiz ko'p bo'lsa-da, ketma-ket natural sonlardan iborat faqat bitta uchlik mavjud. Sirkul va o‘lchagich yordamida irratsional uzunliklarga ega bo‘lgan segmentlarni (yoki irratsional abssissalar bilan koordinatali chiziqdagi nuqtalarni) qurish nafaqat darslik matnida (85-bet) muhokama qilinishi, balki haqiqatda ham bajarilishi maqsadga muvofiqdir. har bir talaba o'z daftarida. Bunday ishni, masalan, uy vazifasi sifatida taklif qilish mumkin. Talabalarga chizma toza, etarlicha katta va "o'qilishi" oson bo'lishi kerakligi haqida ogohlantirish kerak. Keling, darsliklardagi muammoli materialni tahlil qilaylik va "Kvadrat ildizlar" mavzusida qo'llaniladigan masalalarning asosiy turlarini ajratib ko'rsatamiz. Maqolada G.V.ning darsligidan "Kvadrat ildizlar" mavzusidagi mashqlar ta'kidlangan. Dorofeev, mavzuning ushbu kirish qismining barcha muhim jihatlarini qamrab olgan. Mashqlarning asosiy maqsadi - yangi tushunchani o'zlashtirish va radikal belgidan foydalanish qobiliyatini rivojlantirish. Vazifalarga e'tibor qaratiladi va 7. a=b ko'rinishdagi tenglikdan b = a va aksincha tenglikka o'tish qobiliyati juda tez-tez talab qilinadi. Mashqlar 8- - kvadrat ildizlarni o'z ichiga olgan raqamli va alifbo ifodalarining qiymatlarini hisoblash uchun. Talabalar ildiz belgisi qavslar kabi guruhlash belgisi ekanligini bilishlari kerak. 4-7-mashqlarda formulalar bilan avval boshlangan (va amaliy jihatdan juda muhim) ish yanada rivojlantiriladi. Endi bular radikallarni o'z ichiga olgan yoki har qanday o'zgaruvchini boshqalar bilan ifodalashda radikallardan foydalanishni talab qiladigan formulalardir. Bunday topshiriqlar ko'pincha o'quvchilarga qiyinchilik tug'diradi, shuning uchun ularni quyidagi fikrlarni o'rganish orqali qisman bajarish mumkin. 1 dan tashqari

Bundan tashqari, ularga qaytish foydalidir. Bu bosqichda B guruhining 8 va 9-topshiriqlari qiyin deb hisoblanadi; Ular, albatta, barcha talabalar uchun emas. Tayyorgarlik darajasi past boʻlgan sinflarda “A” guruhining topshiriqlarini, iloji boʻlsa, 41 va 44. Darslikdagi misolni koʻrib chiqing: 60 ning taxminiy qiymatini toping. Yechish: Sonning kvadrati ilova qilingan. ikkita "aniq" kvadratlar orasida - 49 va 64: 49 raqamlari<(60), то есть 7 <(60) <8. Значит как 7 <(60), то 7< 60; так как (60) <8, то 60<8. Значит 7< 60<8. Очевидно, что 60 ближе к 8, чем к 7, то есть Рассмотренный способ нахождения приближенного значения корня, в силу своей громоздкости, имеет, в основном, теоретическое значение; учащимся достаточно лишь уметь указывать два целых числа, между которыми заключено значение данного корня. А при решении задач предполагается широкое использование калькулятора. Упражнения к пункту предназначены, прежде всего, для осознанного восприятия этого сложного для учащихся материала (46-51). Кроме того, использование калькулятора позволяет, с помощью наблюдений, прийти к некоторым теоретическим обобщениям, например к выводу о возрастании значения корня с увеличением подкоренного выражения (5-54). В образце к упражнению 6 показаны приемы сравнения, которыми должны овладеть учащиеся. Упражнения 65 и 66 направлены на формирование умения выполнять преобразование выражений, содержащих квадратные корни, с использованием равенства (a) =а, где a 0. В классах с невысоким уровнем подготовки достаточно упражнений группы А. Вообще, в этом блоке дана представительная группа заданий,

23, bu butunlay cheklanishi mumkin. 57-mashq. I-usul. Kalkulyatordan foydalanib, ildizlarning taxminiy qiymatlarini toping: 5.4; 6,45; 7.65. Bu shuni anglatadiki, bu raqamlarning har biri uchlari nuqtalarda va bo'lgan segmentga tegishli bo'lib, ular ushbu segmentda quyidagi tartibda joylashgan: 5, 6, 7. Keyinchalik: 5 raqami uchlari nuqtalarda bo'lgan segmentga tegishli va, ; 6 raqami 4 va 5 nuqtalarda uchlari bo'lgan segmentga tegishli; 7 raqami 6 va 7 nuqtalarda uchlari bo'lgan segmentga tegishli. II usul. Biz xuddi shunday natijaga taxmin yordamida erishamiz. Masalan, 5 uchun bizda:<(5) <, то есть < 5<;, <(5) <, то есть,< 5<,. Упражнение 59. Очевидно, что точке К соответствует число 0,4, так как 0< 0,4< 1. Точно так же легко понять, что число лишнее, так как на отрезке с концами х=1 и х точка не отмечена. Сложнее с точкой L: ведь каждое из оставшихся чисел 5 и 7 располагается на отрезке с концами и. Но точка L расположена в левой половине отрезка, значит число, которое ей соответствует, должно быть меньше,5. Ответ почти очевиден: это 5. Но все же какое-то объяснение необходимо. Можно обратиться к калькулятору, а можно рассуждать так:,5 = 6,5; так как (5) <,5, то 5 <,5. Упражнение 70. а) Сначала находим, что 8< 7,5 < 9, а затем сравниваем числа 8,5 и 7,5. Так как 8,5 = 7,5<7,5, то 8,5< 7,5,

24 va bu 7,5 raqami 9 ga yaqinroq degan ma'noni anglatadi. Muammolarni hal qilishda, tabiiyki, siz kalkulyatordan foydalanasiz deb taxmin qilinadi. A guruhidan tayyorgarlik darajasi past bo'lgan sinflarda siz o'zingizni vazifalar bilan cheklashingiz mumkin (ular majburiy talablar darajasiga javob beradi), shuningdek, tadqiqot muammosini ko'rib chiqing 91. 86-mashq. Muammo darslikning 7-rasmiga asoslanib echiladi. Vizual fikrlardan ko'rinib turibdiki, eng katta uzunlikdagi segment parallelepipedning diagonali hisoblanadi. Diagonal uzunligini qamish uzunligi bilan solishtiramiz. Birinchidan, asos diagonali l uzunligini topamiz: l= a + b = = 700 (sm). Endi parallelepiped d diagonalining uzunligini topamiz: d= (700) + 50 = 9800 (sm). 9800 yildan beri< 10000=100, то трость данных размеров поместить в коробку нельзя. Упражнение 90. Геометрически выражение a + b + c можно истолковать как длину диагонали прямоугольного параллелепипеда, измерения которого a, b и с. В самом деле, из прямоугольного треугольника LMN имеем, что LM= a + b. А из прямоугольного треугольника KLN получим, что NM= c + (a + b) = a + b + c По неравенству треугольника a + b + c

25 10= + 1 ; 1= + ; 17= Lekin buni boshqacha qilish mumkin. Shunday qilib, 10 uzunlikdagi segmentni quyidagi algoritm yordamida olish mumkin: 10 = (5) + (5). 8-sinf uchun algebra darsligida Muravina mualliflari bo‘limni o‘rganishni quyidagi mashqlardan boshlashni taklif qiladilar: 15-mashq. Y=x funksiya grafigi nuqtadan o‘tadimi: A(-;4) B(- .5;1) C(;59) D (-6,5;4,5). Javob: A-ha, B-yo‘q C-ha D-ha. 17-bandda kvadrat ildizni hisoblash uchun mashqlar mavjud.Misol. Hisoblang Yechim 1105 sonining tub omillarga parchalanishi orqali yuzaga keladi. 1105= *5 * = 5 7 = (5 7) =*5*7=105 Javob: 105. 18-bandda arifmetik kvadrat ildizlarning xossalari va ularni qo‘llash, radikal ifodalarni soddalashtirish va hisoblash vazifalari keltirilgan. 4-misol. (100-bet) Soddalashtiring (5). (5) = - 5 = 5-. Javob: 5-. 5-misol. 0, = 0, =0,8*4*5=80 ni hisoblang. Javob 80. 6-misol. Hisoblang = =4 7. Javob: 4 7. 19-bandda ildiz belgisi ostidagi koʻpaytuvchini qoʻshish va ayirish mashqlari koʻrib chiqilib, iboralar qiymatlarini solishtirish boʻyicha topshiriqlar ham koʻrib chiqiladi. . 5

26 7-misol. Ifodada ildiz belgisi ostidagi koeffitsientni olib tashlang 10 va 90 sonlarini tub ko‘rsatkichlarga ajratamiz: 10= **5, 90=* *5. Demak, 10*90= 4 * * = 4 5 = **5* =60. Javob: =,5.. Javob:,5. 8-misol. (105-bet) Ifodani soddalashtiring = 5 = 5 = 9-misol. (105-bet) Ildiz belgisi ostidagi omilni kiriting: 5 0,4. 5 0,4 = 5 0,4 = 5 0,4 = 10. Javob: 10. 10-misol. (106-bet) va iboralarining ma’nolarini solishtiring. = 9 = 18 va = 4 = 1. >. Javob: >. 0 nuqta kvadrat ildizli amallar, kvadrat ildizli kasrlarni aylantirish, ifodalarni soddalashtirish, irratsionallikdan xalos bo'lishga bag'ishlangan. 11-misol. (108-bet) 54 kasrni uning maxrajida radikal bo‘lmasligi uchun aylantiring. Javob: = 54 = 1 7 = 1 = 4= =. 9 1-misol. (109-bet) Ifodani soddalashtiring =5 6 96=4 6 = = = =() 6=1 6 Javob:

27 1-misol. (109-bet) Kasrni maxrajdagi irratsionallikdan ozod qiling. =(). Javob: (). 6 = 6(1+ 10) 1 10 (1 10)(1+ 10) =6(1+ 10) = 6(1+ 10) =. Tayanch maktab algebrasi kursida “Kvadrat ildizlar” mavzusini o‘qitish shakllari, usullari va vositalari.Ushbu bo‘limda mavzuni o‘rganish bo‘yicha amaliy tajribani nashr etilgan maqolalar va o‘quv qo‘llanmalar asosida tahlil qilamiz. S.Minaevaning maqolasida ta’kidlanganidek, o‘rganilayotgan kursda kvadrat ildiz tushunchasi ikkita masalani – geometrik (uning maydoniga qarab kvadrat tomonining uzunligini topish haqidagi) va algebraik masalalarni muhokama qilishda “paydo bo‘ladi”. (x = a ko'rinishdagi tenglamaning ildizlari soni haqida, bu erda a ixtiyoriy son ). Birinchi masalani ko'rib chiqish munosabati bilan o'quvchilar irratsional sonlar haqida dastlabki g'oyalarni oladilar. Bobning mazmuniga muallif algebra uchun noan'anaviy savol - Pifagor teoremasini kiritdi. Bu segmentlar uzunligini topish, irratsional uzunlikdagi segmentlar va irratsional koordinatali nuqtalarni qurish uchun kvadrat ildizlardan tabiiy foydalanishni ko'rsatish uchun qilingan. Shu bilan birga, talabalar Pifagor teoremasini birinchi marta qaerdan eshitishlari muhim emas - geometriya kursida yoki algebra kursida. Muallif, shuningdek, ta'limning eng muhim natijasi, g'oyaviy jihatlardan tashqari, kvadrat ildizlarni (birinchi navbatda, sonli) o'z ichiga olgan iboralarni ba'zi o'zgartirishlarni amalga oshirish qobiliyatidir. Talabalar kub ildizlari tushunchasi bilan ham tanishadilar; shu bilan birga, ular 7 ildizi haqida dastlabki fikrlarni shakllantiradilar

28-darajali. Nihoyat, mashqlar tizimi orqali talabalar y = x va y = x grafiklari haqida tushunchaga ega bo'ladilar. Mavzu davomida muallif kalkulyatordan nafaqat ildizlarni olish vositasi, balki muayyan nazariy g'oyalarni tasvirlash vositasi sifatida ham keng foydalanishni nazarda tutadi. Kub ildizlarini olish uchun kalkulyatordan foydalanish zarurati tufayli n musbat sonning ildizi uchun boshqa belgi kiritiladi: a = a 1 n. V.Olxovning maqolasida "Kvadrat ildizlar" bo'limini o'rganishda murakkab radikalni o'zgartirishga alohida e'tibor berish kerakligiga e'tibor qaratiladi. Muallif mavzuni o'rganishda talaba bilan ishlashning individual shakliga misol keltirgan holda quyidagi metodologiyani taklif qiladi: Matematika sinfidagi o'quvchidan x - 7x + 10 tenglamasining ildizlarini tanlash yo'li bilan topish uchun Vyeta teoremasidan foydalanish so'ralgan. = 0, buni u juda qiyinchiliksiz bajardi: X 1 = 5, X = (savolning soddaligi meni biroz xafa qildi). Keyin 7 ± 10 ifodasini soddalashtirish taklif qilindi. Bu erda biz radikal ostida to'liq kvadratni ko'rishimiz kerak. Oldindan A ± B = A A B ± A A B formulasini yozib, (1) unga aniq raqamli qiymatlarni qo'ydi va ± = 5 ± ni oldi. Ammo oldingi misol bilan to'g'ridan-to'g'ri o'xshashlik mavjud 7=5 +, 10=5*, ya'ni 7 ± 10= 5 + ± 5 = (5 ±) = 5 ± Shundan so'ng, talaba mustaqil ravishda bir nechta misollarni hal qildi: 8

29 6 ± 4 = 6 ± 8 = 4 + ± 4 =±, 1 ± 48= 1 ± 1 = ± 1 1= 1 ± 1, 18 ± 18= 18 ± = 16 + ± 16 =4±, 7 ± 4 = 7 ± 1 = 4 + ± 4 =± va formula (1) qanday paydo bo'lganini endi tushunganini aytdi, lekin uni maxsus eslab qolish shart emas. A ± B= A ± B 4. Tenglama tuzamiz: X AX + B = 0. 4 X 1 = A+ A B, X = A A B ; A ± B= A ± B 4 = X 1 + X ± X 1 X = X 1 ± X = A+ A B ± A A B, bu yerda A>0, B>0, A -B>0 va formula A bo‘lganda soddalashtiriladi. - Aniq kvadratda. Mashq 1. Buni ko'rsating = ; = 1 + Maqola muallifi V.I. Sedakova sizning boshingizdagi operatsiyalarni tezda bajarishga imkon beruvchi oddiy usullarni taklif qiladi, masalan, kvadrat ildizlarni olish. Ushbu usullar sinfda samaradorlikni oshirishi mumkin, chunki og'zaki va yarim og'zaki mashqlar darsda katta hajmdagi materialni o'rganishga imkon beradi, bu o'qituvchiga 9-sinfning tayyorgarligini baholashga imkon beradi.

Yangi materialni o'rganish uchun 30. Ushbu material kelajakdagi matematika o'qituvchilari uchun foydalidir. Maktabda matematika kursini o‘qitishning asosiy maqsadlaridan biri o‘quvchilarda ongli va kuchli hisoblash ko‘nikmalarini shakllantirishdan iborat. Hisoblash qobiliyatlari matematik ko'nikmalarning muhim tarkibiy qismidir. Og'zaki arifmetika mavzusi, ayniqsa, davlat yakuniy attestatsiyasi (FSE) va yagona davlat imtihoni (USE) paytida dolzarb bo'lib, bu erda hisoblash qurilmalaridan foydalanishga yo'l qo'yilmaydi. Boshqa ish shakllari bilan birgalikda og'zaki mashqlar o'quvchilar faoliyatining har xil turlari: fikrlash, nutq, vosita ko'nikmalarini faollashtiradigan sharoitlarni yaratishga imkon beradi. Shuning uchun ham har bir matematika darsida aqliy hisob-kitoblar bilan mashq qilish uchun 10 daqiqagacha vaqt ajratish kerak. Hisoblash ko'nikmalarini shakllantirish murakkab va tizimli jarayondir. U quyidagi bosqichlardan iborat: Ko`nikma shakllanishining birinchi bosqichi malakani egallashdir. Ikkinchi bosqich - mahoratni avtomatlashtirish bosqichi. Ko'nikmani avtomatlashtirish - bu mashqlarni og'zaki, amaliy ravishda eslatmalar, eslatmalar va hokazolarsiz bajarishda natijalarga erishishdir. Talabalar uchun “Kvadrat ildizlar” mavzusida aqliy hisoblash usuli bilan tanishtiramiz. Ko'p xonali natural sonning kvadrat ildizini ajratib olish. Birinchidan, natural sonlar bilan ishlashda foydalanish mumkin bo'lgan kvadrat ildizni umumiy shaklda chiqarish algoritmini yozamiz. 1. Raqamni guruhlarga bo'ling (o'ngdan chapga, oxirgi raqamdan boshlab), har bir guruhdagi ikkita qo'shni raqam. Bunday holda, oxirgi guruhda bitta raqam (agar raqam toq sonli raqamlar bo'lsa) va raqamlar soni juft bo'lsa, ikkita raqam bo'lishi mumkin. Bu raqamdagi guruhlar soni natijaning raqamlari sonini ko'rsatadi.

31. Biz eng katta raqamni tanlaymiz, shunda uning kvadrati oxirgi guruhdagi raqamdan oshmaydi (o'ngdan chapga sanab); bu natijaning birinchi raqami.Natijaning birinchi raqamini kvadratga aylantiramiz, natijada olingan sonni oxirgi guruhdan ayirib, o'ngdagi topilgan farqga oxirgidan oldingi guruhni qo'shamiz. Biz ma'lum bir raqamni olamiz A. Natijaning mavjud qismini ikki barobarga oshirib, biz a raqamini olamiz. Endi a va x sonining ko'paytmasi A sonidan oshmasligi uchun x raqamini tanlaymiz. X soni natijaning ikkinchi raqamidir. 4. A sonidan x ga a sonining ko'paytmasini ayirib, o'ng tarafdagi topilgan farqga uchinchi guruhni qo'shing, biz ma'lum B sonni olamiz. Endi eng katta y raqamini shunday tanlaymizki, sonning y ga ko‘paytmasi B sonidan oshmaydi. Y raqami natijaning uchinchi raqamidir. 5. Qoidaning keyingi bosqichi 4-bosqichni takrorlaydi. Bu raqamlarning birinchi guruhi ishlatilgunga qadar davom etadi. 14-misol. Ushbu algoritmni oddiyroq misol yordamida ko'rsatamiz, natijasi aniq. 144 ni hisoblaymiz. Ikki o'nlik ichida natural sonlar kvadratlari jadvalidan ma'lumki 144 = 1. 144 sonida o'ngdan chapga ikkita raqamni ajratamiz, 1/44. Biz ikkita raqam guruhini oldik, natijada ikki xonali raqam bo'ladi. Biz kvadrati ikkinchi guruhdagi raqamdan oshmaydigan raqamni tanlaymiz (o'ngdan chapga sanab), bu raqam 1. Bizning holatlarimizda bu raqam 1 raqami bo'ladi, chunki uning kvadrati birga teng. Demak, javobda o‘nliklar qatorida 1 raqami bo‘ladi.144 raqamidan hosil bo‘lgan o‘nlik sonini ayirib, qolgan 44 raqami bo‘ladi.Javobdagi birliklar sonini aniqlaymiz. Buni amalga oshirish uchun, chap tomonda, olingan o'nlab raqamlarni ko'paytiramiz, biz olamiz. Keling, buni tanlaymiz 1

32 - bu raqam, o'z-o'zidan ko'paytirilsa va natijada 44 bo'ladi. Bu raqam, shuning uchun 144 ning kvadrat ildizini olganda, biz 1 raqamini olamiz. 1_ javobining raqamlarini tanlaymiz. Javob: 144=1. 15-misol. Besh xonali sondan kvadrat ildiz olish jarayonini ko'rib chiqing.Javobning raqamlarini tanlang 4 Javob: 54756=4. Birinchi bob bo'yicha xulosalar 1-bobda "Kvadrat ildizlar" mavzusini o'qitishning asosiy maqsad va vazifalari Federal Davlat Ta'lim Standartlari MChJ va matematika dasturlari asosida asosiy maktabning algebra kursida ko'rib chiqildi. Mavzu bo'yicha 8-sinf uchun algebra darsliklarida nazariy va muammoli materiallar tahlili shuni ko'rsatdiki, darslik mualliflari kvadrat ildiz tushunchasining o'zi va kvadrat ildizlarni hisoblash qobiliyatini rivojlantirishga qaratilgan mashqlar tizimi bilan tanishishda turli xil yondashuvlardan foydalanadilar. sonli ifodalarni soddalashtirish. Maqolalar va o'quv qo'llanmalar asosida "Kvadrat ildizlar" mavzusini o'rganish bo'yicha amaliy tajribani tahlil qilish, mavzu talabalar uchun juda qiyin degan xulosaga kelishimizga imkon beradi. Biroq, tegishli mashqlar va maxsus texnikalar yordamida siz kvadrat ildiz tushunchasi va uning asosiy xususiyatlari haqida mustahkam tushunchaga erishishingiz mumkin.

33 II-BOB. MAKTAB ALGebra fanidan “Kvadrat ildizlar” MAVZUSINI O‘QITISHNI TASHKIL BO‘YICHA METODIK TAVSIYALAR 4. “Kvadrat ildizlar” mavzusi bo‘yicha tayanch maktab algebra kursida bilim va ko‘nikmalarning asosiy darajasiga yo‘naltirilgan “Kvadrat” mavzusi bo‘yicha barcha topshiriqlar. 8-sinf algebra darsliklarida keltirilgan ildizlar” mavzusini shartli ravishda 4 guruhga bo`lish mumkin: 1-guruh.Kvadrat ildizlari bo`lgan ifodalarning ma`nosini topishga oid topshiriqlar. Guruh. Kvadrat tenglamalarni arifmetik kvadrat ildizlar yordamida yechish masalalari. Guruh. Kvadrat ildizli iboralarni soddalashtirish va taqqoslashga oid masalalar. 4-guruh. Kvadrat ildiz masalalari. Masalaning misollarini ko'rib chiqamiz: 1-guruh.Kvadrat ildizlari bo'lgan ifodalarning qiymatini topishga oid masalalar. 1-misol. Ifodaning qiymatini toping: a) 1,5 0,1 0,5 b) 9 c) 16,. Yechish: a) Arifmetik ildizning ta’rifidan kelib chiqadiki, 1,5=.5, chunki,5 > 0 va,5 = 1,5; 0,5= 0,5, chunki 0,5 > 0 va 0,5 = 0,5..5 0,1 0,5 = 7 0,05= 6,95 b) 9 = 9, chunki 9 = 9 = 9

34 c) Bu ifoda ma'noga ega emas, chunki har qanday sonning kvadrati manfiy bo'lmagan sondir. Javob: a) 6,95; b) 9; c) ifoda ma'noga ega emas Misol. Ayiruvchidan irratsionallikni bartaraf qiling: 1 a) 4 b) 7 c) Yechish: 1 a) (1())() 4 1 b) 7 4 (7 4(7)() 7) 4(7 7) 4( 7 4) 7 c) ((5 5 7)(7)(5 5 7) 7) (5 5 7) (5 6) 5 6 (Kasrning maxrajidagi irratsionallikdan qutulishning yangi usuli qoʻllaniladi. - uning konjugati bilan ko'paytirish). Javob: a) + b) 7 + c) 5 6 guruh. Kvadrat tenglamalarni arifmetik kvadrat ildiz yordamida yechish. 10x 14 = 11 ifodadagi x qiymatini toping. 4

35 10x 15 x 1,5 Yechish: 10x x 14 x 15:10 10x x Tekshirish: , Javob: x = 1,5. 4 x x Misol 4. 4 x = 1 ifodadagi x qiymatini toping. Yechish: x 1 Tekshirish: Javob: x Guruh. Ushbu guruhda biz iboralarni soddalashtirish bo'yicha vazifalarni birlashtiramiz. 5-misol: Ifodani soddalashtiring: 5

36 6 Yechish: Kasrning maxrajidagi irratsionallikdan xalos bo‘lish uchun, agar maxrajda ayirma bo‘lsa, bu kasrning ayirmasi bo‘lsa, uning soni va maxrajini yig‘indiga ko‘paytirish kerak yoki bu kasrning ayirma qismi va maxrajini ayirmaga ko‘paytirish kerak. maxrajda yig‘indi bor) () ())(( ))(() ())(())(())(())((Javob: 4 6 6-misol. Ifodani soddalashtiring: 8 4 Yechish: Javob: 6 Misol 7. Ifodani soddalashtiring: .5 8 Yechish: .5 8 (Ko‘paytmaning arifmetik kvadrat ildizidan foydalanadi.) Javob: 5

37 4-guruh. kvadrat ildiz. Bu guruhda chiqarish masalalarini taklif qilamiz 8-misol. Ifodaning ildizini ajratib oling Yechish: 5a 6 49 Kasrning arifmetik kvadrat ildizini chiqarish haqidagi teoremadan foydalanamiz. 5a a a a a 7 6 Mahsulotning arifmetik kvadrat ildizini chiqarish haqidagi teoremadan foydalanamiz. 5a a a a 6 Keyin quyidagi teoremadan foydalanamiz: har qanday a soni uchun quyidagi tenglik bajariladi: a a a 5a 5a 5 a 5 (a) 5 a 5 a Javob: Agar a 0 boʻlsa, a.< 0, то 5 a 7 5 a a 5 7 a Пример 9. Внести множитель под знак корня (буквами обозначены положительные числа): 1) a a 1) x x 5 7

38 1) a Yechish: a a a a a a (Ko‘paytmaning arifmetik kvadrat ildizini qarama-qarshi yo‘nalishda olish teoremasi qo‘llaniladi).) x x x x x x x x (Kuslamaning arifmetik kvadrat ildizini qarama-qarshi yo‘nalishda olish teoremasi qo‘llaniladi). Javob: 1) a) x 11x 4 1) 64 10-misol. Ildizni ajratib oling: x) 400 a, bu yerda a< 0 Решение: 1) 11x x x 4 11 (x 8) 11 x 8 11x 8 1 x 8) 400 a a a a 0 a (Используется теорема об извлечении арифметического квадратного корня из дроби, теорема об извлечении арифметического квадратного корня из произведения и теорема: a a). Ответ: 1) 1 x 8 0 a 8

39 Maqolada ildizlar bilan raqamli ifodalarni soddalashtirishga qaratilgan ko'p o'lchovli didaktik materiallar (kartalardagi vazifalar) taklif etiladi. Mustaqil yoki test ishlarini tashkil qilishda ular matematika o`qituvchisiga shubhasiz yordam beradi. Keling, variantlarning topshiriqlarini beramiz. 1-variant 1. Soddalashtiring: Soddalashtiring: Maxrajdagi irratsionallikni bartaraf qiling: Ifodani soddalashtiring Hisoblang: 7 * 6+4 ifodani soddalashtiring 4, Ifoda qiymatini toping 8. Hisoblang: * Ifodaning qiymatini toping 10. Soddalash ()(75 7) ifodasini toping va natijada olingan son x 0 = 0 tenglamaning ildizi ekanligini isbotlang. Variant 1. Soddalashtiring:

8-SINF UCHUN ALGEBRA FANIDAN ISHCHI DASTUR (umumiy ta’lim darajasi) Tuzuvchi: Tixonov V.A., matematika o‘qituvchisi; Dasturni amalga oshirish muddati: 1 yil Ish dasturi federalga asoslangan

MATEMATIKA bo'yicha tushuntirish yozuvi Ushbu ish dasturi asosiy umumiy ta'limning Davlat ta'lim standarti va asosiy umumiy ta'lim dasturining Federal komponenti asosida ishlab chiqilgan.

Penza shahridagi 30-sonli MBOU o'rta maktabida matematika bo'yicha asosiy umumiy ta'lim ish dasturi (5-sinf) Tushuntirish xati Hujjat holati 5-sinf uchun matematika bo'yicha asosiy umumiy ta'lim ish dasturi

5-sinf uchun matematika bo'yicha ish dasturi uchun referat. Tushuntirish yozuvi 5-sinfda 2016-2017 o'quv yili uchun matematika bo'yicha ish dasturi quyidagilar asosida tuzilgan: 1. Federal qonun 273-Federal qonun 29/12/2012

Tushuntirish yozuvi Matematika bo'yicha ish dasturi quyidagi me'yoriy hujjatlar va uslubiy tavsiyalar asosida tuzilgan: 1. Asosiy fanlar bo'yicha federal davlat ta'lim standarti.

Tushuntirish eslatmasi. Ushbu ish dasturi 8-sinf o'quvchilariga mo'ljallangan va quyidagi hujjatlar asosida amalga oshiriladi:. Boshlang'ich umumiy, asosiy umumiy va ikkinchi darajali davlat standarti

Ishchi o'quv rejasi MATEMATIKA 5-6-sinflar 2017-2018 o'quv yili ANNOMA Ushbu ishchi dastur Federal Davlat Ta'lim kodeksining asosiy qoidalariga muvofiq ishlab chiqilgan.

Belgorodning "17-sonli o'rta maktab" munitsipal byudjet ta'lim muassasasi "kelishilgan" Ta'lim maktabi rahbari N.A. Ilminskaya 20-sonli bayonnoma "Kelishilgan" direktor o'rinbosari

5-sinf uchun matematika bo'yicha ish dasturi IZOH 5-sinf o'quvchilari uchun matematika bo'yicha ish dasturi Rossiya Federatsiyasi Mudofaa vazirligi tomonidan tasdiqlangan Rossiya Federatsiyasi Mudofaa vazirligining 2007 yildagi dasturi va mualliflik huquqi asosida ishlab chiqilgan.

Moskva viloyati yig'ilishida ko'rib chiqildi, madaniy va MKOU LSOSH 1 texnologik faoliyat o'qituvchilari direktori M.M. Kostin va SPL xizmati Buyurtma 109-daqiqa 01 01 sentyabr 2017 yil. 2017 yil 01 sentyabrdan

Asosiy umumiy ta'limning asosiy ta'lim dasturiga ilova, 208 yil 30 avgustdagi 488os buyrug'i. Tyumen viloyati Xanti-Mansi avtonom okrugi Yugra Nijnevartovsk tumani shahar byudjeti

1. Tushuntirish xati 9-sinf uchun algebra bo'yicha ish dasturi me'yoriy hujjatlar va axborot-uslubiy materiallar asosida tuzilgan: 1. Rossiya Federatsiyasida ta'lim bo'yicha: Federal

8-sinf uchun algebra fanidan o'quv materialini kalendar-tematik rejalashtirish. Tushuntirish xati 8-sinf uchun algebra fanidan kalendar-tematik rejalashtirish namunaviy dastur asosida tuzilgan.

Boshlang'ich umumiy ta'lim o'quvchilarining tayyorgarlik darajasiga qo'yiladigan talablar: Talabalar bilishi/tushunishi kerak: - matematika fanining nazariya va amaliyotda yuzaga keladigan masalalarni yechishdagi ahamiyatini; kenglik va bir vaqtning o'zida

ISH DASTURI 8 ta o‘quv kursi o‘rganiladigan sinf (daraja) Fan sohasi Matematika va informatika O‘quv fani Matematika (algebra) 2017-2018 o‘quv yili Yillik soatlar soni 102

Ximki shahridagi 4-gimnaziya shahar byudjeti ta'lim muassasasi TASDIQLANGAN: MBOU 4-gimnaziya direktori / N.N. Kozelskaya / 2015 yil buyrug'i Algebra fanidan ish dasturi (asosiy daraja) 8-sinf

Maktab pedagogik kengashining 2009 yilgi yig‘ilishida ko‘rib chiqilgan.“Kelishilgan” Maktab direktorining MBOSHI “KSHI” ta’lim muassasasi bo‘yicha o‘rinbosari Minnexanova G.R. 2009 yil “Tasdiqlangan” MBOSHI “KSHI” direktori Taipova A.R. 2009 yil

KO'RIB ETILGAN: Moskva viloyati yig'ilishida / ZYUMurtazaeva Pr dan KUZILGAN: Ta'lim muassasalari bo'yicha direktor o'rinbosari / E.K.Xayretdinova TASDIQLANGAN: Maktab direktori / LMAmetova Pr dan ISH DASTURI 8 A MBOUda algebra fanidan "Starokrymskaya Osh"

Tarkib. Tushuntirish xati 3 bet o‘quv fanining o‘quv rejasidagi o‘rni tavsifi o‘quv-uslubiy majmua fanni o‘zlashtirishning rejalashtirilgan natijalari nazorat shakllari 2. O‘quv mavzularining mazmuni

SHAHAR BUDJETT TA'LIM MASSASI 40-LIPETSK NOMOTIDAGI O'RTA TA'LIM MAKTABI Eshitishda nuqsoni bo'lgan 8-sinf o'quvchilari uchun ALGEBRA FANIDAN ISHCHIQ DASTURI.

Tushuntirish yozuvi Umumta'lim muassasasining 8-sinf o'quvchilari uchun "Algebra" o'quv fanining ushbu ish dasturi asosiy umumiy ta'limning mualliflik dasturi asosida ishlab chiqilgan.

Tushuntirish eslatmasi Asosiy o'rta maktabning 8-sinfi uchun ushbu algebra dasturi asosiy umumiy ta'lim davlat standartining federal komponenti asosida tuzilgan.

1. O‘quv fanini o‘zlashtirishning rejalashtirilgan natijalari 6-sinfda “Matematika” fanini o‘rganishning fan natijalari quyidagi ko‘nikmalarni shakllantirish hisoblanadi: “Arifmetika” fan sohasi: bajarish.

Matematika bo'yicha ish dasturiga ilova Murmansk viloyati, Kola tumani, p. Minkino davlat viloyat budjet ta’lim muassasasi “Minkino tuzatish maktab-internati”

Matematika 6-sinf uchun ish dasturi. 1. Kalendar-mavzuiy dars ishlanmasi Mashg’ulot bo’limlari va mavzulari Sana Soatlar soni Birinchi chorak (42 dars) 1. Sonlarning bo’linishi (20 ta dars) 1.09-28.09 1-3 Bo’luvchilar.

REJAJLANGAN NATIJALAR Shaxsiy metamavzu Mavzu fan va texnikaning universal tili, hodisa va jarayonlarni modellashtirish vositasi sifatidagi matematikaning g'oyalari va usullari haqidagi dastlabki g'oyalar;

1 IZOH 9-sinfda "Algebra" fanidan ish dasturi asosiy umumiy ta'lim davlat standartining federal komponenti asosida tuzilgan. Bu ish dasturi

Tushuntirish eslatmasi 8-sinf algebra uchun ish dasturi boshlang'ich umumiy, asosiy umumiy va o'rta (to'liq) umumiy davlat ta'lim standartining Federal komponentiga mos keladi.

Tushuntirish yozuvi Ish dasturi quyidagilar asosida tuzilgan: - matematika bo'yicha asosiy umumiy ta'lim davlat ta'lim standartining federal komponenti - matematika bo'yicha namunaviy dasturlar.

Bob ALGEBRAGA KIRISH.. Kvadrat uch AYoL... Ularning yigindisi va kopaytmasidan ikkita sonni topishning Bobil masalasi. Algebraning eng qadimgi muammolaridan biri Bobilda taklif qilingan va u erda keng tarqalgan

Tushuntirish eslatmasi. Umumta’lim muassasasining 6-sinf o‘quvchilari uchun “Matematika” fanidan ushbu ish dasturi mualliflik dasturi asosida S.M. Nikolskiy, M.K. Potapov,

IZOH. (Matematika 5-sinf) Ushbu ish dasturi Rossiya Federatsiyasi Ta'lim vazirligining umumta'lim muassasalari uchun matematika bo'yicha Davlat dasturiga muvofiq tuzilgan.

Tushuntirish yozuvi Algebra bo'yicha ish dasturi quyidagi me'yoriy-huquqiy hujjatlar asosida ishlab chiqilgan: 2012 yil 29 dekabrdagi 273-FZ "Rossiya Federatsiyasida ta'lim to'g'risida" Federal qonuni; Buyurtma

Tushuntirish yozuvi 8-sinf uchun algebra bo'yicha ish dasturi ikkinchi avlod asosiy umumiy ta'lim bo'yicha Federal davlat ta'lim standarti qoidalariga muvofiq tuzilgan,

Hujjat holati tushuntirish xati Asosiy umumiy ta'lim maktabining 8-sinfi (ilg'or daraja) uchun algebra bo'yicha ushbu ish dasturi shtatning federal komponenti asosida tuzilgan.

Ko'rib chiqilgan Qabul qilingan Moskva matematika o'qituvchilari assotsiatsiyasi tomonidan yig'ilishda tasdiqlangan O'rta maktab shahar ta'lim muassasasi direktori 26.08.2008 yildagi 1-bayonnoma. 2014. pedagogik s. Poima Mudofaa vazirligi boshlig'i Praslova O.M. Kengash Rodionova O.I. Protokol 1

1-son “Sputnik” litseyi xususiy ta’lim muassasasi ko‘rib chiqildi 1 “Sputnik” litsey uslubiy Kengashi yig‘ilishida Bayonnoma 2017-yil. “Sputnik” 1-litseyi uslubiy kengashi raisi Ursul

Ish dasturiga konspekt 8-sinf, algebra IZOH 8-sinf asosiy o'rta maktab uchun algebra fanidan ish dasturi quyidagilar asosida tuzilgan: Davlatning federal komponenti.

1. Tushuntirish xati. Algebra ish dasturi “Algebra 8-sinf” mualliflik dasturi asosida tuzilgan. avto Makarychev va boshqalar davlat komponentining ta'lim fanlari mazmuniga muvofiq

2018 2019 O'QUV YILI 7 "A" SINF UCHUN ALGEBRA VA GEOMETRIYA FANIDAN ISH DASTURI Dastur ishlab chiquvchi o'qituvchi Viktor Aleksandrovich Palenniy 2018 Ish dasturining o'ziga xos xususiyatlari: Moslashtirilgan holda

Munitsipal byudjet ta'lim muassasasi 4-o'rta maktab Pedagogik kengash tomonidan ko'rib chiqilgan 31.08.2008 yildagi 1-bayonnoma. 2017 yil 31.08.2017 yildagi 162-sonli buyrug'i TASDIQLANGAN: Direktor

2018 yilda matematika bo'yicha oraliq attestatsiya uchun sinov va o'lchov materiallari, 7-sinf Tushuntirish yozuvi Ishning mazmuni Rossiya Federatsiyasi Federal qonuniga muvofiq tuzilgan.

Tushuntirish eslatmasi Normativ hujjatlar Ish dasturi quyidagilar asosida tuzilgan: Rossiya Federatsiyasining 9..0 73-FZ-sonli "Rossiya Federatsiyasida ta'lim to'g'risida" Federal qonuni federal komponenti

Tushuntirish yozuvi Ish dasturi quyidagilar asosida tuzilgan: Rossiya Federatsiyasi Ta'lim vazirligining 03.05.2004 yildagi 1089-sonli "Davlat ta'lim standartlarining federal komponentini tasdiqlash to'g'risida" gi buyrug'i.

1. FANNI O‘ZLASHTIRISHNING REJALDAGI NATIJALARI Boshlang‘ich sinflarda matematika fanini o‘rganish o‘quvchilarga quyidagi natijalarga erishish imkonini beradi: Shaxsni rivojlantirish yo‘nalishida: - aniq, aniq,

IZOH 8-sinf uchun algebra ish dasturi ikkinchi avlod asosiy umumiy ta'lim bo'yicha Federal davlat ta'lim standarti qoidalariga muvofiq tuzilgan,

8-sinfda algebra fanidan TAQVIM MAVZUVIY REJAJLASH o'quv dasturiga ilova "ALGEBRA 8" darsligi, muallifi Yu.N.Makarychev va boshqalar, S.A.Telyakovskiy tahriri O'qituvchi: Dudnikova

Tushuntirish yozuvi Boshlang'ich maktab uchun algebra dasturi quyidagi talablarga muvofiq tuzilgan: - asosiy umumiy ta'lim davlat ta'lim standartining federal komponenti

Tushuntirish eslatmasi 8-sinf uchun algebra bo'yicha ish dasturi (chuqur o'rganish) davlat ta'lim standartining federal komponentiga, algebra dasturiga muvofiq tuzilgan.

ROSSIYA FEDERATSIYASI TA'LIM VA FAN VAZIRLIGI NOVOSIBIRSK DAVLAT UNIVERSITETI MAXSUS TA'LIM VA TADQIQOT MARKAZI Matematika 8-sinf Ko'p nomli Novosibirsk ko'p nomli Ratsional

Ish dasturi me'yoriy hujjatlarga muvofiq tuziladi:. "Rossiya Federatsiyasida ta'lim to'g'risida" gi 29.2.202 yil 273-FZ Federal qonuni, Federal davlat ta'lim muassasasining talablari.

Tushuntirish yozuvi Ushbu "Algebra" ish dasturi quyidagilar asosida ishlab chiqilgan: - 2012 yil 29 dekabrdagi 273-FZ Federal qonuni (2015 yil 13 iyuldagi tahrirda) "Rossiya Federatsiyasida ta'lim to'g'risida"; - mualliflik huquqi asosida

Ish dasturi me'yoriy hujjatlarga muvofiq tuzilgan: "Rossiya Federatsiyasida ta'lim to'g'risida" gi 29.2.202 273-FZ-sonli federal qonun. 2. Rossiya Federatsiyasi Ta'lim va fan vazirligining buyrug'i

Qozog'iston Respublikasi Umumiy va kasbiy ta'lim vazirligi

davlat byudjeti ta'lim muassasasi

Rostov viloyatidagi boshlang'ich kasb-hunar ta'limi

5-sonli kasb-hunar maktabi

Amaliy ish

EDP ​​intizomi bo'yicha. 01.“Matematika: algebra va tamoyillar

matematik tahlil; geometriya"

ushbu mavzu bo'yicha: “Ildiz, daraja va logarifmlarni o'z ichiga olgan iboralarni o'zgartirish».

Uchun talabalar I kurs

G. Rostov-na-Donu

2017 yil

№1 bo'lim. Algebra.

1.2-mavzu. Ildizlar, kuchlar va logarifmlar.

Amaliy dars № 1.

Mavzu: "Ildiz, daraja va logarifmlarni o'z ichiga olgan iboralarni o'zgartirish."

Maqsad: bilish radikallar, darajalar va logarifmlarning xossalari; qachon ularni qo'llash imkoniyatiga ega bo'lish ildizlar, darajalar va logarifmlarni o'z ichiga olgan iboralar ustida o'zgartirishlarni amalga oshirish.

Soatlar soni : 1 soat.

Nazariy material.

Ildizlar.

Ildiz topilgan harakatn-chi daraja, ildiz chiqarish deb ataladin- daraja.

Ta'rif. Tabiiy darajaning arifmetik ildizin≥ 2 manfiy bo'lmagan a soni manfiy bo'lmagan son deb ataladi,nuning th darajasi a ga teng.

Ikkinchi darajali arifmetik ildiz kvadrat ildiz, uchinchi darajali ildiz esa kub ildiz deyiladi.

Masalan.

Hisoblash:

Arifmetik ildizn- daraja quyidagi xususiyatlarga ega:

a ≥ 0 bo'lsa, b > 0 va n, m- natural sonlar, van ≥ 2, m≥ 2, keyin

1. 3.

2. 4.

Arifmetik ildiz xossalaridan foydalanishga misollar.

Ratsional darajali daraja xossalari.

Har qanday p va k ratsional sonlar va har qanday a > 0 va b > 0 uchun tengliklar to‘g‘ri bo‘ladi:

1. ; 2. ;

3. ; 4. ;

5. .

Darajaning xususiyatlaridan foydalanishga misollar:

1). 7*

4). .

Raqamning logarifmi

Ta'rif. Musbat sonning logarifmiba asosiga, qaerdaa > 0, a≠ 1, sonni ko'tarish kerak bo'lgan ko'rsatkich deyiladia, olish uchun b.

a = b asosiy logarifmik identifikatsiya hisoblanadi.

Logarifmlarning xossalari

Mayli a > 0, a ≠ 1, b>0, c >0, k – har qanday haqiqiy son. Keyin formulalar amal qiladi:

1 . jurnal ( miloddan avvalgi ) = logb + logc , 4. logb = ,

2. log = logb - log c, 5.jurnal a = 1 ,

3. jurnal b = ga * logb , 6. jurnal 0 = 1 .

Formulalardan foydalanishga misollar:

log2 + log 18 = jurnal ( 2 * 18 ) = jurnal 36 = 2;

jurnal 48 - log 4 = jurnal= jurnal 12 = 1;

jurnal 9 = * jurnal 9 = .

O'zingiz uchun qaror qiling .

Vazifalar.

1 variant

1. Hisoblang:

1) ; 4) jurnal ;

2) ; 5) 0,5;

3) ; 6) 3 jurnal 2 - jurnal 64.

2, agar x = 7 bo'lsa.

3. Raqamlarni solishtiring:jurnal 11 va jurnal 19.

4. Soddalashtiring: 1) ; 2) .

5. Hisoblang: jurnaljurnaljurnal 3.

_________________________________________________________________

Variant 2

1. Hisoblang:

1) ; 4) jurnal 64;

2) ; 5) ;

3) ; 6) 2 jurnal 3 - jurnal 81.

2. Ifodaning ma'nosini toping: 3, agar y = 2 bo'lsa.

3. Raqamlarni solishtiring:jurnal Va jurnal.

4. Soddalashtiring: 1) ; 2) .

5. Hisoblang: jurnaljurnaljurnal 2.

__________________________________________________________________

Baholash mezonlari:

11 ta to'g'ri topshiriq - "5";

9 - 10 ta to'g'ri topshiriq - "4";

7 - 8 ta to'g'ri topshiriq - "3".

Bashmakov. M.I. Matematika: NPO va DSP uchun darslik. - M.:

"Akademiya" nashriyot markazi, 2013 yil.

Alimov Sh.A. va boshqalar.Algebra va analizning boshlanishi. 10 (11) hujayra – M.: 2012 yil.

Algebra. 9-sinf: Umumta’lim uchun darslik, muammoli kitob. muassasalar/

A.G. Mordkovich va boshqalar - M.: Mnemosyne, 2009.

Algebra. 8-sinf: Umumta’lim uchun darslik, muammoli kitob. muassasalar/

A.G. Mordkovich va boshqalar - M.: Mnemosyne, 2008.

Algebra. 7-sinf: Umumta’lim uchun darslik, muammoli kitob. muassasalar/

A.G. Mordkovich va boshqalar - M.: Mnemosyne, 2007.

Hisobot shakli: o'qituvchi tomonidan topshiriqlarning bajarilishini tekshirish

Amalda ildiz chiqarish operatsiyasidan muvaffaqiyatli foydalanish uchun siz ushbu operatsiyaning xususiyatlari bilan tanishishingiz kerak.
Barcha xususiyatlar faqat ildiz belgilari ostida joylashgan o'zgaruvchilarning salbiy bo'lmagan qiymatlari uchun tuzilgan va tasdiqlangan.

Teorema 1. Ikki manfiy bo‘lmagan chiplar ko‘paytmasining n-chi ildizi (n=2, 3, 4,...) bu sonlarning n- ildizlari ko‘paytmasiga teng:

Izoh:

1. Radikal ifoda ikkitadan ortiq manfiy bo'lmagan sonlarning ko'paytmasi bo'lgan holatda 1-teorema o'z kuchida qoladi.

Teorema 2.Agar, n esa 1 dan katta natural son bo‘lsa, tenglik to‘g‘ri bo‘ladi

Qisqacha(noto'g'ri bo'lsa ham) amalda qo'llash qulayroq bo'lgan formula: kasrning ildizi ildizlarning ulushiga teng.

1-teorema t ni ko'paytirishga imkon beradi faqat bir xil darajadagi ildizlar , ya'ni. faqat bir xil indeksli ildizlar.

Teorema 3.Agar ,k natural son va n natural son 1 dan katta bo'lsa, tenglik to'g'ri bo'ladi

Boshqacha qilib aytganda, ildizni tabiiy kuchga ko'tarish uchun radikal ifodani bu kuchga ko'tarish kifoya.
Bu 1-teoremaning natijasidir. Aslida, masalan, k = 3 uchun biz quyidagilarni olamiz: k ko'rsatkichining boshqa har qanday natural qiymatida ham xuddi shunday fikr yurita olamiz.

Teorema 4.Agar ,k, n - 1 dan katta natural sonlar, u holda tenglik to'g'ri bo'ladi

Boshqacha qilib aytganda, ildizdan ildiz olish uchun ildizlarning ko'rsatkichlarini ko'paytirish kifoya.
Masalan,

Diqqatli bo'ling! Biz ildizlar ustida to'rtta amalni bajarish mumkinligini bilib oldik: ko'paytirish, bo'lish, darajaga ko'tarish va ildiz chiqarish (ildizdan). Ammo ildizlarni qo'shish va ayirish haqida nima deyish mumkin? Bo'lishi mumkin emas.
Masalan, Really yozish o'rniga, lekin bu aniq

Teorema 5.Agar ildiz va radikal ifodaning ko'rsatkichlari bir xil natural songa ko'paytiriladi yoki bo'linadi, keyin ildizning qiymati o'zgarmaydi, ya'ni.

Muammoni hal qilishga misollar

1-misol. Hisoblash

Yechim. Ildizlarning birinchi xossasidan (1-teorema) foydalanib, biz quyidagilarni olamiz:

2-misol. Hisoblash
Yechim. Aralash sonni noto'g'ri kasrga aylantiring.
Bizda ildizlarning ikkinchi xususiyatidan foydalanish ( Teorema 2 ), biz olamiz:

3-misol. Hisoblash:

Yechim. Algebradagi har qanday formula, siz yaxshi bilganingizdek, nafaqat "chapdan o'ngga", balki "o'ngdan chapga" ham qo'llaniladi. Demak, ildizlarning birinchi xossasi ularning shaklda ifodalanishi va aksincha, ifoda bilan almashtirilishini bildiradi. Xuddi shu narsa ildizlarning ikkinchi xususiyatiga ham tegishli. Buni hisobga olib, hisob-kitoblarni amalga oshiramiz.

Tabriklaymiz: bugun biz ildizlarni ko'rib chiqamiz - 8-sinfdagi eng aqlga sig'maydigan mavzulardan biri. :)

Ko'pchilik ildizlar haqida ular murakkab bo'lgani uchun emas (bu juda murakkab narsa - bir nechta ta'riflar va yana bir nechta xususiyatlar), chunki ko'pchilik maktab darsliklarida ildizlar shunday o'rmon orqali aniqlanadiki, faqat darslik mualliflari. bu yozuvni o'zlari tushunishlari mumkin. Va shunga qaramay, faqat bir shisha yaxshi viski bilan. :)

Shuning uchun, endi men ildizning eng to'g'ri va eng malakali ta'rifini beraman - siz haqiqatan ham eslashingiz kerak bo'lgan yagona ta'rif. Va keyin men tushuntiraman: bularning barchasi nima uchun kerak va uni amalda qanday qo'llash kerak.

Ammo birinchi navbatda, ko'plab darslik tuzuvchilari negadir "unutib qo'yadigan" muhim narsani unutmang:

Ildizlar juft darajali (bizning sevimli $\sqrt(a)$, shuningdek, barcha turdagi $\sqrt(a)$ va hatto $\sqrt(a)$) va toq darajali (barcha $\sqrt) bo'lishi mumkin. (a)$, $\ sqrt(a)$ va boshqalar). Va toq darajadagi ildizning ta'rifi juftdan biroz farq qiladi.

Ehtimol, ildizlar bilan bog'liq bo'lgan barcha xatolar va tushunmovchiliklarning 95% bu "biroz boshqacha" da yashiringan. Shunday qilib, keling, terminologiyani bir marta va butunlay tozalaymiz:

Ta'rif. Hatto ildiz n$a$ raqamidan istalgan salbiy bo'lmagan$b$ soni shundayki, $((b)^(n))=a$. Xuddi shu $a$ sonining toq ildizi, odatda, bir xil tenglikka ega boʻlgan har qanday $b$ soni: $((b)^(n))=a$.

Har holda, ildiz quyidagicha belgilanadi:

\(a)\]

Bunday yozuvdagi $n$ soni ildiz ko‘rsatkichi, $a$ soni esa radikal ifoda deyiladi. Xususan, $n=2$ uchun biz “sevimli” kvadrat ildizimizni olamiz (darvoqe, bu juft darajali ildiz), $n=3$ uchun esa kub ildizni (toq daraja) olamiz. masalalar va tenglamalarda ham tez-tez uchraydi.

Misollar. Kvadrat ildizlarning klassik misollari:

\[\begin(align) & \sqrt(4)=2; \\ & \sqrt(81)=9; \\ & \sqrt(256)=16. \\ \end (tekislash)\]

Aytgancha, $\sqrt(0)=0$ va $\sqrt(1)=1$. Bu juda mantiqiy, chunki $((0)^(2))=0$ va $((1)^(2))=1$.

Kub ildizlari ham keng tarqalgan - ulardan qo'rqishning hojati yo'q:

\[\begin(align) & \sqrt(27)=3; \\ & \sqrt(-64)=-4; \\ & \sqrt(343)=7. \\ \end (tekislash)\]

Xo'sh, bir nechta "ekzotik misollar":

\[\begin(align) & \sqrt(81)=3; \\ & \sqrt(-32)=-2. \\ \end (tekislash)\]

Agar siz juft va toq daraja o'rtasidagi farq nima ekanligini tushunmasangiz, ta'rifni qayta o'qing. Bu juda muhim!

Shu bilan birga, biz ildizlarning bir noxush xususiyatini ko'rib chiqamiz, shuning uchun biz juft va toq ko'rsatkichlar uchun alohida ta'rifni kiritishimiz kerak edi.

Nima uchun ildizlar umuman kerak?

Ta'rifni o'qib chiqqandan so'ng, ko'plab talabalar: "Matematiklar buni o'ylab topganlarida nima chekishgan?" Va haqiqatan ham: nima uchun bu ildizlar umuman kerak?

Bu savolga javob berish uchun keling, bir zum boshlang'ich maktabga qaytaylik. Yodingizda bo'lsin: o'sha uzoq vaqtlarda, daraxtlar yashil va chuchvara mazali bo'lganida, bizning asosiy tashvishimiz raqamlarni to'g'ri ko'paytirish edi. Xo'sh, "beshga besh - yigirma besh" kabi bir narsa, bu hammasi. Ammo siz raqamlarni juftlikda emas, balki uchlik, to'rtlik va umuman butun to'plamlarda ko'paytirishingiz mumkin:

\[\begin(align) & 5\cdot 5=25; \\ & 5\cdot 5\cdot 5=125; \\ & 5\cdot 5\cdot 5\cdot 5=625; \\ & 5\cdot 5\cdot 5\cdot 5\cdot 5=3125; \\ & 5\cdot 5\cdot 5\cdot 5\cdot 5\cdot 5=15\ 625. \end(align)\]

Biroq, bu masala emas. Ayyorlik boshqacha: matematiklar dangasa odamlardir, shuning uchun ular o‘n beshning ko‘payishini shunday yozishda qiynalgan:

Shuning uchun ular ilmiy darajalar bilan kelishdi. Nega omillar sonini uzun satr o'rniga yuqori chiziq sifatida yozmaslik kerak? Shunga o'xshash narsa:

Bu juda qulay! Barcha hisob-kitoblar sezilarli darajada kamayadi va siz 5183 ni yozish uchun bir nechta pergament varaqlari va daftarlarni behuda sarflashingiz shart emas. Ushbu rekord raqamning kuchi deb ataldi, unda bir qancha xususiyatlar topildi, ammo baxt qisqa muddatli bo'lib chiqdi.

Darajalar “kashfiyoti” uchun uyushtirilgan dabdabali ziyofatdan so‘ng, ayniqsa qaysar matematik birdan: “Agar biz raqamning darajasini bilsak-u, lekin raqamning o‘zi noma’lum bo‘lsa-chi?” deb so‘radi. Haqiqatan ham, agar biz ma'lum bir $b $ soni, aytaylik, 5-darajaga 243 ni berishini bilsak, $b $ sonining o'zi nimaga teng ekanligini qanday taxmin qilishimiz mumkin?

Bu muammo birinchi qarashda ko'rinadiganidan ancha global bo'lib chiqdi. Chunki ko'pchilik "tayyor" kuchlar uchun bunday "dastlabki" raqamlar yo'qligi ma'lum bo'ldi. O'zingiz uchun hukm qiling:

\[\begin(align) & ((b)^(3))=27\Rightarrow b=3\cdot 3\cdot 3\Rightarrow b=3; \\ & ((b)^(3))=64\O'ng strelka b=4\cdot 4\cdot 4\O'ng strelka b=4. \\ \end (tekislash)\]

$((b)^(3))=50$ bo'lsa-chi? Ma'lum bo'lishicha, biz ma'lum bir raqamni topishimiz kerak, uni uch marta ko'paytirganda bizga 50 ni beradi. Lekin bu raqam nima? Bu aniq 3 dan katta, chunki 3 3 = 27< 50. С тем же успехом оно меньше 4, поскольку 4 3 = 64 >50. Ya'ni bu raqam uchdan to'rtgacha bo'lgan joyda yotadi, lekin siz nimaga teng ekanligini tushunolmaysiz.

Aynan shuning uchun matematiklar $n$th ildizlarini o'ylab topishgan. Aynan shuning uchun $\sqrt(*)$ radikal belgisi kiritildi. $b $ raqamini belgilash uchun, bu ko'rsatilgan darajada bizga oldindan ma'lum bo'lgan qiymatni beradi

\[\sqrt[n](a)=b\O'ng strelka ((b)^(n))=a\]

Men bahslashmayman: ko'pincha bu ildizlar osongina hisoblab chiqiladi - biz yuqorida bir nechta bunday misollarni ko'rdik. Ammo shunga qaramay, ko'p hollarda, agar siz o'zboshimchalik bilan raqamni o'ylab ko'rsangiz va undan ixtiyoriy darajaning ildizini olishga harakat qilsangiz, siz dahshatli baxtsizlikka duch kelasiz.

Nima bor! Hatto eng oddiy va eng tanish $\sqrt(2)$ ni ham odatiy shaklda - butun son yoki kasr sifatida ifodalab bo'lmaydi. Va agar siz ushbu raqamni kalkulyatorga kiritsangiz, buni ko'rasiz:

\[\sqrt(2)=1,414213562...\]

Ko'rib turganingizdek, kasrdan keyin hech qanday mantiqqa bo'ysunmaydigan raqamlarning cheksiz ketma-ketligi mavjud. Siz, albatta, boshqa raqamlar bilan tezda solishtirish uchun bu raqamni yaxlitlashingiz mumkin. Masalan:

\[\sqrt(2)=1,4142...\taxminan 1,4 \lt 1,5\]

Yoki yana bir misol:

\[\sqrt(3)=1,73205...\taxminan 1,7 \gt 1,5\]

Ammo bu yaxlitlashlarning barchasi, birinchi navbatda, juda qo'pol; va ikkinchidan, siz taxminiy qiymatlar bilan ham ishlashingiz kerak, aks holda siz bir qator noaniq xatolarga duch kelishingiz mumkin (Aytgancha, taqqoslash va yaxlitlash mahorati Yagona davlat imtihonining profilida sinovdan o'tishi kerak).

Shuning uchun jiddiy matematikada siz ildizlarsiz qilolmaysiz - ular bizga uzoq vaqtdan beri tanish bo'lgan kasrlar va butun sonlar kabi $\mathbb(R)$ barcha haqiqiy sonlar to'plamining bir xil teng vakillaridir.

Ildizni $\frac(p)(q)$ ko’rinishdagi kasr sifatida ifodalay olmaslik bu ildizning ratsional son emasligini bildiradi. Bunday raqamlar irratsional deb nomlanadi va ularni aniq ifodalash mumkin emas, faqat buning uchun maxsus mo'ljallangan radikal yoki boshqa konstruktsiyalar (logarifmlar, kuchlar, chegaralar va boshqalar). Ammo bu haqda boshqa safar.

Keling, barcha hisob-kitoblardan keyin irratsional sonlar javobda qoladigan bir nechta misollarni ko'rib chiqaylik.

\[\begin(align) & \sqrt(2+\sqrt(27))=\sqrt(2+3)=\sqrt(5)\taxminan 2,236... \\ & \sqrt(\sqrt(-32) ))=\sqrt(-2)\taxminan -1,2599... \\ \end(align)\]

Tabiiyki, ildizning ko'rinishidan kasrdan keyin qanday raqamlar kelishini taxmin qilish deyarli mumkin emas. Biroq, siz kalkulyatorga ishonishingiz mumkin, lekin hatto eng ilg'or sana kalkulyatori bizga faqat irratsional sonning birinchi bir necha raqamlarini beradi. Shuning uchun javoblarni $\sqrt(5)$ va $\sqrt(-2)$ ko`rinishlarida yozish ancha to`g`riroq.

Aynan shuning uchun ular ixtiro qilingan. Javoblarni qulay tarzda yozib olish uchun.

Nima uchun ikkita ta'rif kerak?

Diqqatli o'quvchi, ehtimol, misollarda keltirilgan barcha kvadrat ildizlar ijobiy raqamlardan olinganligini payqagandir. Xo'sh, hech bo'lmaganda noldan. Ammo kub ildizlarini har qanday raqamdan xotirjamlik bilan olish mumkin - bu ijobiy yoki salbiy.

Nima uchun bu sodir bo'lmoqda? $y=((x)^(2))$ funksiya grafigiga qarang:

Kvadrat funksiya grafigi ikkita ildiz beradi: musbat va manfiy

Keling, ushbu grafik yordamida $\sqrt(4)$ ni hisoblashga harakat qilaylik. Buning uchun grafikda (qizil rang bilan belgilangan) gorizontal $y=4$ chiziladi, u parabola bilan ikkita nuqtada kesishadi: $((x)_(1))=2$ va $((x) )_(2)) =-2$. Bu juda mantiqiy, chunki

Birinchi raqam bilan hamma narsa aniq - bu ijobiy, shuning uchun ildiz:

Ammo ikkinchi nuqta bilan nima qilish kerak? To'rttaning bir vaqtning o'zida ikkita ildizi bormi? Axir, agar −2 sonini kvadratga aylantirsak, biz ham 4 ni olamiz. Nima uchun u holda $\sqrt(4)=-2$ yozmaslik kerak? Va nega o'qituvchilar bunday postlarga sizni yemoqchi bo'lgandek qarashadi? :)

Muammo shundaki, agar siz qo'shimcha shartlar qo'ymasangiz, unda to'rtta ikkita kvadrat ildizga ega bo'ladi - ijobiy va salbiy. Va har qanday ijobiy raqam ham ulardan ikkitasiga ega bo'ladi. Ammo manfiy sonlar umuman ildizga ega bo'lmaydi - buni bir xil grafikdan ko'rish mumkin, chunki parabola hech qachon o'qdan pastga tushmaydi. y, ya'ni. salbiy qiymatlarni qabul qilmaydi.

Xuddi shunday muammo teng ko'rsatkichli barcha ildizlar uchun yuzaga keladi:

1. To'g'rirog'i, har bir musbat sonning $n$ ko'rsatkichli ikkita ildizi bo'ladi;
2. Salbiy raqamlardan hatto $n$ bo'lgan ildiz umuman chiqarilmaydi.

Shuning uchun ham $n$ juft darajali ildizni ta'riflashda javob manfiy bo'lmagan son bo'lishi kerakligi alohida ko'rsatilgan. Shunday qilib, biz noaniqlikdan xalos bo'lamiz.

Lekin g'alati $n$ uchun bunday muammo yo'q. Buni ko‘rish uchun $y=((x)^(3))$ funksiya grafigini ko‘rib chiqamiz:

Kub parabolasi har qanday qiymatni qabul qilishi mumkin, shuning uchun kub ildizi istalgan raqamdan olinishi mumkin

Ushbu grafikdan ikkita xulosa chiqarish mumkin:

1. Kub parabolaning shoxlari oddiydan farqli o'laroq, ikkala yo'nalishda ham - yuqoriga ham, pastga ham cheksizlikka boradi. Shuning uchun, biz gorizontal chiziqni qanday balandlikda chizmasak ham, bu chiziq bizning grafigimiz bilan kesishadi. Binobarin, kub ildizi har doim mutlaqo istalgan raqamdan olinishi mumkin;
2. Bundan tashqari, bunday kesishma har doim o'ziga xos bo'ladi, shuning uchun qaysi raqam "to'g'ri" ildiz deb hisoblanishi va qaysi birini e'tiborsiz qoldirish haqida o'ylashingiz shart emas. Shuning uchun toq daraja uchun ildizlarni aniqlash juft darajaga qaraganda oddiyroqdir (salbiy bo'lmasligi shart emas).

Ko‘pchilik darsliklarda bu oddiy narsalar tushuntirilmagani achinarli. Buning o'rniga, bizning miyamiz har xil arifmetik ildizlar va ularning xususiyatlari bilan ko'tarila boshlaydi.

Ha, men bahslashmayman: arifmetik ildiz nima ekanligini ham bilishingiz kerak. Va men bu haqda alohida darsda batafsil gaplashaman. Bugun biz bu haqda ham gaplashamiz, chunki usiz $n$-inchi ko'plikning ildizlari haqidagi barcha fikrlar to'liq bo'lmaydi.

Lekin birinchi navbatda siz yuqorida bergan ta'rifni aniq tushunishingiz kerak. Aks holda, atamalarning ko'pligi tufayli sizning boshingizda shunday tartibsizlik boshlanadiki, oxirida siz hech narsani tushunmaysiz.

Sizga kerak bo'lgan yagona narsa - juft va toq ko'rsatkichlar o'rtasidagi farqni tushunish. Shuning uchun, keling, yana bir bor ildizlar haqida bilishingiz kerak bo'lgan hamma narsani to'playmiz:

1. Juft darajali ildiz faqat manfiy bo'lmagan sondan mavjud bo'lib, o'zi hamisha manfiy bo'lmagan sondir. Salbiy sonlar uchun bunday ildiz aniqlanmagan.
2. Ammo g'alati darajaning ildizi har qanday sondan mavjud bo'lib, o'zi ham har qanday raqam bo'lishi mumkin: musbat sonlar uchun u musbat, manfiy sonlar uchun esa, shapka ko'rsatganidek, manfiy.

Bu qiyinmi? Yo'q, qiyin emas. Tushunarli? Ha, bu mutlaqo aniq! Endi biz hisob-kitoblar bilan biroz mashq qilamiz.

Asosiy xususiyatlar va cheklovlar

Ildizlar juda ko'p g'alati xususiyatlar va cheklovlarga ega - bu alohida darsda muhokama qilinadi. Shuning uchun, endi biz faqat teng indeksli ildizlarga tegishli bo'lgan eng muhim "hiyla" ni ko'rib chiqamiz. Bu xususiyatni formula sifatida yozamiz:

\[\sqrt(((x)^(2n)))=\chap| x\right|\]

Boshqacha qilib aytadigan bo'lsak, agar biz raqamni juft darajaga ko'tarsak va keyin bir xil darajaning ildizini chiqarsak, biz asl sonni emas, balki uning modulini olamiz. Bu osonlik bilan isbotlanishi mumkin bo'lgan oddiy teorema (salbiy bo'lmagan $x$ ni alohida, keyin esa manfiylarni alohida ko'rib chiqish kifoya). O'qituvchilar bu haqda doimo gapiradilar, bu har bir maktab darsligida berilgan. Ammo irratsional tenglamalarni (ya'ni, radikal belgisi bo'lgan tenglamalarni) yechish haqida gap ketganda, talabalar bir ovozdan bu formulani unutishadi.

Muammoni batafsil tushunish uchun keling, barcha formulalarni bir daqiqaga unutib, ikkita raqamni to'g'ridan-to'g'ri hisoblashga harakat qilaylik:

\[\sqrt(((3)^(4)))=?\quad \sqrt(((\left(-3 \o'ng))^(4)))=?\]

Bular juda oddiy misollar. Ko'pchilik birinchi misolni hal qiladi, lekin ko'p odamlar ikkinchisiga yopishib olishadi. Bunday axlatni muammosiz hal qilish uchun har doim protsedurani ko'rib chiqing:

1. Birinchidan, raqam to'rtinchi darajaga ko'tariladi. Xo'sh, bu qandaydir oson. Siz hatto ko'paytirish jadvalida ham topilishi mumkin bo'lgan yangi raqamni olasiz;
2. Va endi bu yangi raqamdan to'rtinchi ildizni olish kerak. Bular. ildizlar va kuchlarning "kamayishi" sodir bo'lmaydi - bu ketma-ket harakatlar.

Birinchi ifodani ko'rib chiqamiz: $\sqrt(((3)^(4)))$. Shubhasiz, siz avval ildiz ostidagi ifodani hisoblashingiz kerak:

\[((3)^(4))=3\cdot 3\cdot 3\cdot 3=81\]

Keyin 81 raqamining to'rtinchi ildizini chiqaramiz:

Endi ikkinchi ifoda bilan ham xuddi shunday qilamiz. Birinchidan, biz −3 sonini to'rtinchi darajaga ko'taramiz, bu esa uni o'z-o'zidan 4 marta ko'paytirishni talab qiladi:

\[((\left(-3 \o'ng))^(4))=\left(-3 \o'ng)\cdot \left(-3 \o'ng)\cdot \left(-3 \o'ng)\cdot \ chap (-3 \o'ng)=81\]

Biz ijobiy raqamni oldik, chunki mahsulotdagi minuslarning umumiy soni 4 tani tashkil etadi va ularning barchasi bir-birini bekor qiladi (oxir-oqibat, minus uchun minus plyus beradi). Keyin yana ildizni chiqaramiz:

Aslida, bu qatorni yozish mumkin emas edi, chunki javob bir xil bo'lishi aqlga sig'maydi. Bular. Xuddi shu teng quvvatning teng ildizi minuslarni "yoqadi" va bu ma'noda natija oddiy moduldan farq qilmaydi:

\[\begin(align) & \sqrt(((3)^(4)))=\left| 3 \right|=3; \\ & \sqrt(((\left(-3 \o'ng))^(4)))=\chap| -3 \o'ng|=3. \\ \end (tekislash)\]

Bu hisob-kitoblar juft darajali ildizning ta'rifi bilan yaxshi mos keladi: natija har doim manfiy bo'lmaydi va radikal belgi ham har doim manfiy bo'lmagan sonni o'z ichiga oladi. Aks holda, ildiz aniqlanmagan.

Jarayon haqida eslatma

1. $\sqrt(((a)^(2)))$ belgisi birinchi navbatda $a$ raqamini kvadratga aylantirib, keyin olingan qiymatning kvadrat ildizini olishimizni bildiradi. Shuning uchun, ildiz belgisi ostida har doim manfiy bo'lmagan son mavjudligiga ishonch hosil qilishimiz mumkin, chunki har qanday holatda $((a)^(2))\ge 0$;
2. Lekin $((\left(\sqrt(a) \right))^(2))$ yozuvi, aksincha, biz avval ma'lum $a$ sonning ildizini olamiz va shundan keyingina natijani kvadratga olamiz. Shuning uchun $a$ soni hech qanday holatda salbiy bo'lishi mumkin emas - bu ta'rifga kiritilgan majburiy talab.

Shunday qilib, hech qanday holatda ildizlar va darajalarni o'ylamasdan qisqartirmaslik kerak va shu bilan asl iborani "soddalashtirish" mumkin. Chunki agar ildiz manfiy songa ega bo'lsa va uning ko'rsatkichi juft bo'lsa, biz bir qator muammolarni olamiz.

Biroq, bu muammolarning barchasi faqat hatto ko'rsatkichlar uchun ham tegishli.

Ildiz belgisi ostidagi minus belgisini olib tashlash

Tabiiyki, ko'rsatkichlari toq bo'lgan ildizlar ham o'ziga xos xususiyatga ega, ular printsipial jihatdan juftlarda mavjud emas. Aynan:

\[\sqrt(-a)=-\sqrt(a)\]

Qisqacha aytganda, g'alati darajadagi ildizlar belgisi ostidan minusni olib tashlashingiz mumkin. Bu barcha kamchiliklarni "tashqariga tashlash" imkonini beruvchi juda foydali xususiyat:

\[\begin(align) & \sqrt(-8)=-\sqrt(8)=-2; \\ & \sqrt(-27)\cdot \sqrt(-32)=-\sqrt(27)\cdot \left(-\sqrt(32) \o'ng)= \\ & =\sqrt(27)\cdot \sqrt(32)= \\ & =3\cdot 2=6. \end(tuzalash)\]

Ushbu oddiy xususiyat ko'plab hisob-kitoblarni sezilarli darajada osonlashtiradi. Endi tashvishlanishingizga hojat yo'q: agar salbiy ibora ildiz ostida yashiringan bo'lsa-chi, lekin ildizdagi daraja teng bo'lib chiqdi? Ildizlardan tashqaridagi barcha minuslarni "tashlab qo'yish" kifoya qiladi, shundan so'ng ular bir-biriga ko'paytirilishi, bo'linishi va umuman olganda, "klassik" ildizlar holatida bizni olib kelishi kafolatlangan ko'plab shubhali narsalarni qilishlari mumkin. xato.

Va bu erda yana bir ta'rif paydo bo'ladi - xuddi shu ta'rif ko'pchilik maktablarda irratsional iboralarni o'rganishni boshlaydi. Va busiz bizning fikrimiz to'liq bo'lmaydi. Tanishing!

Arifmetik ildiz

Keling, bir lahzaga taxmin qilaylik, ildiz belgisi ostida faqat ijobiy raqamlar yoki o'ta og'ir holatlarda nol bo'lishi mumkin. Keling, juft/toq ko'rsatkichlarni unutaylik, yuqorida keltirilgan barcha ta'riflarni unutaylik - biz faqat manfiy bo'lmagan raqamlar bilan ishlaymiz. Keyin nima?

Va keyin biz arifmetik ildizga ega bo'lamiz - bu bizning "standart" ta'riflarimiz bilan qisman mos keladi, lekin baribir ulardan farq qiladi.

Ta'rif. $a$ manfiy boʻlmagan sonning $n$-chi darajali arifmetik ildizi manfiy boʻlmagan $b$ son boʻlib, $((b)^(n))=a$ boʻladi.

Ko'rib turganimizdek, endi bizni paritet qiziqtirmaydi. Buning o'rniga yangi cheklov paydo bo'ldi: radikal ifoda endi har doim salbiy emas va ildizning o'zi ham salbiy emas.

Arifmetik ildiz odatdagidan qanday farq qilishini yaxshiroq tushunish uchun biz allaqachon tanish bo'lgan kvadrat va kub parabola grafiklarini ko'rib chiqing:

Arifmetik ildiz qidirish maydoni - manfiy bo'lmagan raqamlar

Ko'rib turganingizdek, bundan buyon bizni faqat birinchi koordinata choragida joylashgan grafik qismlari qiziqtiradi - bu erda $x$ va $y$ koordinatalari ijobiy (yoki hech bo'lmaganda nolga teng). Manfiy raqamni ildiz ostiga qo'yish huquqiga egamiz yoki yo'qligini tushunish uchun endi indikatorga qarash kerak emas. Chunki manfiy raqamlar endi printsipial jihatdan hisobga olinmaydi.

Siz shunday deb so'rashingiz mumkin: "Xo'sh, nega bizga bunday ta'rif kerak?" Yoki: "Nega biz yuqorida keltirilgan standart ta'rifga erisha olmaymiz?"

Xo'sh, men faqat bitta xususiyatni beraman, shuning uchun yangi ta'rif mos keladi. Masalan, eksponentsiya qoidasi:

\[\sqrt[n](a)=\sqrt(((a)^(k)))\]

Iltimos, diqqat qiling: biz radikal ifodani istalgan kuchga ko'tarishimiz va shu bilan birga ildiz ko'rsatkichini bir xil kuchga ko'paytirishimiz mumkin - natijada bir xil raqam bo'ladi! Mana misollar:

\[\begin(align) & \sqrt(5)=\sqrt(((5)^(2)))=\sqrt(25) \\ & \sqrt(2)=\sqrt(((2)^ (4)))=\sqrt(16)\\ \end(align)\]

Xo'sh, nima katta ish? Nega biz buni oldin qila olmadik? Mana nima uchun. Oddiy ifodani ko'rib chiqaylik: $\sqrt(-2)$ - bu raqam bizning klassik tushunchamizda juda normal, ammo arifmetik ildiz nuqtai nazaridan mutlaqo qabul qilinishi mumkin emas. Keling, uni aylantirishga harakat qilaylik:

$\begin(align) & \sqrt(-2)=-\sqrt(2)=-\sqrt(((2)^(2))))=-\sqrt(4) \lt 0; \\ & \sqrt(-2)=\sqrt(((\left(-2 \o'ng))^(2)))=\sqrt(4) \gt 0. \\ \end(align)$

Ko'rib turganingizdek, birinchi holatda biz minusni radikal ostidan olib tashladik (bizda barcha huquqlar bor, chunki ko'rsatkich g'alati), ikkinchi holatda biz yuqoridagi formuladan foydalandik. Bular. Matematik nuqtai nazardan, hamma narsa qoidalarga muvofiq amalga oshiriladi.

WTF?! Qanday qilib bir xil raqam ham ijobiy, ham salbiy bo'lishi mumkin? Bo'lishi mumkin emas. Shunchaki, musbat sonlar va nol uchun ajoyib ishlaydigan eksponentatsiya formulasi salbiy sonlar holatida to'liq bid'atni keltirib chiqara boshlaydi.

Bunday noaniqlikdan xalos bo'lish uchun arifmetik ildizlar ixtiro qilindi. Ularga alohida katta dars bag'ishlangan bo'lib, unda biz ularning barcha xususiyatlarini batafsil ko'rib chiqamiz. Shuning uchun biz hozir ular haqida to'xtalmaymiz - dars juda uzoq bo'lib chiqdi.

Algebraik ildiz: ko'proq bilishni istaganlar uchun

Bu mavzuni alohida paragrafga qo'yamanmi yoki yo'qmi, uzoq o'yladim. Oxir-oqibat, men uni shu erda qoldirishga qaror qildim. Ushbu material ildizlarni yaxshiroq tushunishni istaganlar uchun mo'ljallangan - endi o'rtacha "maktab" darajasida emas, balki Olimpiada darajasiga yaqin.

Demak: sonning $n$-inchi ildizining “klassik” ta’rifi va unga bog‘liq bo‘lgan juft va toq ko‘rsatkichlarga bo‘linishidan tashqari, paritet va boshqa nozikliklarga umuman bog‘liq bo‘lmagan ko‘proq “kattalar” ta’rifi mavjud. Bu algebraik ildiz deyiladi.

Ta'rif. Har qanday $a$ ning $n$-inchi algebraik ildizi $((b)^(n))=a$ boʻladigan barcha $b$ sonlar toʻplamidir. Bunday ildizlar uchun aniq belgi yo'q, shuning uchun biz tepaga chiziqcha qo'yamiz:

\[\overline(\sqrt[n](a))=\left\( b\left| b\in \mathbb(R);((b)^(n))=a \o'ng. \o'ng\) \]

Dars boshida berilgan standart ta’rifdan tub farqi shundaki, algebraik ildiz aniq son emas, balki to‘plamdir. Va biz haqiqiy raqamlar bilan ishlaganimiz sababli, bu to'plam faqat uchta turda bo'ladi:

1. Bo'sh to'plam. Manfiy sondan juft darajali algebraik ildizni topish kerak bo'lganda paydo bo'ladi;
2. Bitta elementdan iborat to'plam. Toq darajalarning barcha ildizlari, shuningdek, nolning juft darajalarining ildizlari shu toifaga kiradi;
3. Nihoyat, to'plam ikkita raqamni o'z ichiga olishi mumkin - biz ko'rgan $((x)_(1))$ va $((x)_(2))=-((x)_(1))$ kvadratik funksiya grafigi. Shunga ko'ra, bunday tartibga solish faqat musbat sondan juft darajaning ildizini chiqarganda mumkin.

Oxirgi holat batafsilroq ko'rib chiqishga loyiqdir. Farqni tushunish uchun bir nechta misollarni sanab o'tamiz.

Misol. Ifodalarni baholang:

\[\overline(\sqrt(4));\quad \overline(\sqrt(-27));\quad \overline(\sqrt(-16)).\]

Yechim. Birinchi ifoda oddiy:

\[\overline(\sqrt(4))=\left\( 2;-2 \o'ng\)\]

Bu to'plamning bir qismi bo'lgan ikkita raqam. Chunki ularning har birining kvadrati to'rtlikni beradi.

\[\overline(\sqrt(-27))=\chap\( -3 \o'ng\)\]

Bu erda biz faqat bitta raqamdan iborat to'plamni ko'ramiz. Bu juda mantiqiy, chunki ildiz ko'rsatkichi g'alati.

Nihoyat, oxirgi ifoda:

\[\overline(\sqrt(-16))=\varnothing \]

Biz bo'sh to'plam oldik. Chunki to'rtinchi (ya'ni, hatto!) darajaga ko'tarilganda bizga -16 manfiy sonini beradigan bitta haqiqiy son yo'q.

Yakuniy eslatma. E'tibor bering: biz haqiqiy raqamlar bilan ishlayotganimizni hamma joyda ta'kidlaganim yo'q. Chunki murakkab raqamlar ham bor - u erda $\sqrt(-16)$ va boshqa ko'plab g'alati narsalarni hisoblash juda mumkin.

Biroq, zamonaviy maktab matematika kurslarida murakkab raqamlar deyarli hech qachon paydo bo'lmaydi. Ular aksariyat darsliklardan olib tashlangan, chunki bizning rasmiylar mavzuni "tushunish juda qiyin" deb hisoblashadi.

Ana xolos. Keyingi darsda biz ildizlarning barcha asosiy xususiyatlarini ko'rib chiqamiz va nihoyat irratsional ifodalarni qanday soddalashtirishni o'rganamiz. :)