Mashq qilish.
da x ning qiymatini toping.

Yechim.
Funktsiya argumentining qaysidir qiymatga teng bo'lgan qiymatini topish, qaysi argumentlar uchun sinusning qiymati shartda ko'rsatilgandek bir xil bo'lishini aniqlashni anglatadi.
Bunday holda, qanday qiymatlarda sinusning qiymati 1/2 ga teng bo'lishini aniqlashimiz kerak. Buni bir necha usul bilan amalga oshirish mumkin.
Masalan, x ning qaysi qiymatlarida sinus funktsiyasi 1/2 ga teng bo'lishini aniqlash uchun dan foydalaning.
Yana bir usul - foydalanish. Shuni eslatib o'tamanki, sinuslarning qiymatlari Oy o'qida yotadi.
Eng keng tarqalgan usul - bu 1/2 kabi ushbu funktsiya uchun standart qiymatlar haqida gap ketganda.
Barcha holatlarda sinusning eng muhim xususiyatlaridan biri - uning davri haqida unutmaslik kerak.
Keling, jadvaldagi sinusning 1/2 qiymatini topamiz va unga qanday argumentlar mos kelishini ko'rib chiqamiz. Bizni qiziqtirgan dalillar Pi / 6 va 5Pi / 6.
Berilgan tenglamani qanoatlantiradigan barcha ildizlarni yozing. Buning uchun bizni qiziqtirgan noma'lum x argumentini va jadvaldan olingan argumentning qiymatlaridan birini, ya'ni Pi / 6 ni yozamiz. Buning uchun sinus davrini hisobga olgan holda yozamiz, argumentning barcha qiymatlari:

Keling, ikkinchi qiymatni olamiz va oldingi holatda bo'lgani kabi bir xil amallarni bajaramiz:

Dastlabki tenglamaning to'liq yechimi quyidagicha bo'ladi:
Va
q har qanday butun sonning qiymatini qabul qilishi mumkin.

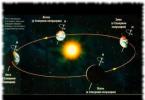
Trigonometrik doirada gradusdagi burchaklardan tashqari biz kuzatamiz.

Radianlar haqida ko'proq ma'lumot:

Radian uzunligi uning radiusiga teng bo'lgan yoyning burchak qiymati sifatida aniqlanadi. Shunga ko'ra, aylana bo'lgani uchun , u holda radian doiraga mos kelishi aniq bo'ladi, ya'ni

1 rad ≈ 57,295779513° ≈ 57°17'44,806″ ≈ 206265″.

Radian ekanligini hamma biladi

Shunday qilib, masalan, a . Bizda shunday Radianlarni burchaklarga aylantirishni o'rganing.

Endi aksincha darajalarni radianga aylantiramiz.

Aytaylik, biz radianga aylantirishimiz kerak. Bizga yordam beradi. Biz quyidagicha harakat qilamiz:

Chunki, radian, keyin jadvalni to'ldiring:

Biz aylanada sinus va kosinus qiymatlarini topishga o'rgatamiz

Keling, quyidagilarga aniqlik kiritaylik.

Xo'sh, agar bizdan hisoblashni so'rashsa yaxshi bo'ladi, aytaylik - odatda bu erda hech qanday chalkashlik yo'q - hamma birinchi bo'lib aylanaga qarashni boshlaydi.

Va agar ulardan hisoblash so'ralsa, masalan, ... Ko'pchilik, to'satdan, bu nolni qayerdan izlash kerakligini tushunolmay boshlaydi ... Ko'pincha ular uni kelib chiqishidan izlaydilar. Nega?

1) Keling, bir marta va umuman rozi bo'laylik! Nima keyin keladi yoki argument = burchak, va bizning burchaklarimiz aylanada, ularni x o'qida qidirmang!(Shunchaki, alohida nuqtalar aylanaga ham, o'qga ham tushadi ...) Va sinuslar va kosinuslarning qiymatlari - biz o'qlarda qidiramiz!

2) Va boshqalar! Agar biz boshlang'ich nuqtadan ketsak soat miliga teskari(trigonometrik doirani chetlab o'tishning asosiy yo'nalishi), keyin burchaklarning ijobiy qiymatlarini chetga surib qo'yamiz, biz bu yo'nalishda harakat qilganimizda burchaklar ortadi.

Agar biz boshlang'ich nuqtadan ketsak soat yo'nalishi bo'yicha, keyin burchaklarning salbiy qiymatlarini chetga surib qo'yamiz.

1-misol

Qiymat toping.

Yechim:

Biz aylanada topamiz. Biz nuqtani sinus o'qiga proyeksiya qilamiz (ya'ni nuqtadan sinus o'qiga (oy) perpendikulyar chizamiz).

Biz 0 ga yetamiz. Demak, .

2-misol

Qiymat toping.

Yechim:

Biz aylana bo'ylab topamiz (biz soat sohasi farqli o'laroq o'tamiz va boshqalar). Biz nuqtani sinus o'qiga proyeksiya qilamiz (va u allaqachon sinus o'qida yotadi).

Biz sinus o'qi bo'ylab -1 ga tushamiz.

E'tibor bering, "yashirin" nuqtaning orqasida (biz belgilangan nuqtaga soat yo'nalishi bo'yicha borishimiz mumkin, ya'ni minus belgisi paydo bo'ladi) va boshqa cheksiz ko'p narsalar.

Quyidagi o'xshashlikni qilish mumkin:

Trigonometrik doirani stadion yugurish yo'lakchasi sifatida tasavvur qiling.

Axir, siz "Bayroq" nuqtasida tugashingiz mumkin, men soat sohasi farqli o'laroq, aytaylik, 300 m yuguraman yoki soat yo'nalishi bo'yicha 100 m yuguraman (biz yo'lning uzunligi 400 m deb hisoblaymiz).

Va shuningdek, soat sohasi farqli o'laroq, masalan, 700 m, 1100 m, 1500 m va hokazolarni yugurib, "Bayroq" nuqtasida ("boshlash" dan keyin) tugashingiz mumkin. Bayroq nuqtasiga soat yo'nalishi bo'yicha 500 yoki 900 m va hokazo yugurish orqali erishishingiz mumkin.

Stadionning yugurish yo'lagini aqliy ravishda raqamlar qatoriga kengaytiring. Tasavvur qiling-a, bu chiziqning qayerida, masalan, 300, 700, 1100, 1500 va hokazo qiymatlar bo'ladi. Biz raqamlar chizig'ida bir-biridan teng masofada joylashgan nuqtalarni ko'ramiz. Keling, orqaga qaytaylik. Nuqtalar bittaga "bir-biriga yopishadi".

Trigonometrik doirada ham shunday. Har bir nuqtaning orqasida cheksiz ko'p boshqa narsalar bor.

Aytaylik, burchaklar, , va hokazo. bitta nuqta sifatida ko'rsatilgan. Va ulardagi sinus, kosinus qiymatlari, albatta, bir xil. (Qoʻshilgan/ayirganimizni payqadingizmi yoki? Bu sinus va kosinus funksiyasi uchun davr.)

3-misol

Qiymat toping.

Yechim:

Keling, oddiylik uchun darajalarga aylantiraylik.

(keyinchalik, trigonometrik doiraga o'rganganingizda, radianlarni darajaga aylantirishingiz shart emas):

Biz nuqtadan soat yo'nalishi bo'yicha harakat qilamiz Yarim aylana () va yana ko'p

Biz sinusning qiymati sinusning qiymatiga to'g'ri kelishini va unga teng ekanligini tushunamiz

E'tibor bering, agar biz masalan, yoki va hokazolarni olsak, biz bir xil sinus qiymatini olamiz.

4-misol

Qiymat toping.

Yechim:

Biroq, biz oldingi misoldagi kabi radianlarni darajaga aylantirmaymiz.

Ya'ni, soat miliga teskari yo'nalishda yarim doira va yarim doiraning yana chorak qismiga o'tishimiz kerak va natijada olingan nuqtani kosinus o'qiga (gorizontal o'q) proyeksiya qilishimiz kerak.

5-misol

Qiymat toping.

Yechim:

Trigonometrik doirada qanday chiziladi?

Agar biz o'tsak yoki ha, hech bo'lmaganda, biz "boshlash" deb belgilagan nuqtaga etib boramiz. Shuning uchun, siz darhol aylananing nuqtasiga o'tishingiz mumkin

6-misol

Qiymat toping.

Yechim:

Biz bir nuqtada yakunlanamiz (baribir bizni nolga olib boradi). Biz aylananing nuqtasini kosinus o'qiga proyeksiya qilamiz (trigonometrik doiraga qarang), biz kiramiz. Ya'ni .

Trigonometrik doira - sizning qo'lingizda

Siz allaqachon tushungansiz, asosiysi birinchi chorakdagi trigonometrik funktsiyalarning qiymatlarini eslab qolishdir. Qolgan choraklarda hamma narsa o'xshash, siz faqat belgilarga amal qilishingiz kerak. Umid qilamanki, siz trigonometrik funktsiyalar qiymatlarining "zanjirli narvonlarini" unutmaysiz.

Qanday topish mumkin tangens va kotangens qiymatlari asosiy burchaklar.

Shundan so'ng, tangens va kotangensning asosiy qiymatlari bilan tanishib, o'tishingiz mumkin

Bo'sh doira shablonida. Poyezd!

Sinus qiymatlari [-1; 1], ya'ni. -1 ≤ sin a ≤ 1. Demak, agar |a| > 1 bo'lsa, sin x = a tenglamaning ildizlari yo'q. Masalan, sin x = 2 tenglamaning ildizlari yo'q.

Keling, ba'zi vazifalarga murojaat qilaylik.

sin x = 1/2 tenglamani yeching.

Yechim.

E'tibor bering, sin x - R (1; 0) nuqtani koordinata atrofida x burchak bilan aylantirish natijasida olingan birlik aylana nuqtasining ordinatasi.

½ ga teng ordinata M 1 va M 2 aylananing ikkita nuqtasida mavjud.

1/2 \u003d sin p / 6 bo'lgani uchun, M 1 nuqtasi P (1; 0) nuqtasidan x 1 \u003d p / 6 burchak orqali, shuningdek x \u003d p burchaklari orqali burilib olinadi. / 6 + 2p, bu erda k \u003d +/-1, +/-2, …

M 2 nuqta P (1; 0) nuqtadan x 2 = 5p/6 burchak orqali, shuningdek, x = 5p/6 + 2pk burchaklar orqali burilish natijasida olinadi, bu erda k = +/- 1, +/-2, ... , ya'ni. burchaklarda x = p – p/6 + 2pk, bu yerda k = +/-1, +/-2, ….

Demak, sin x = 1/2 tenglamaning barcha ildizlarini x = p/6 + 2pk, x = p - p/6 + 2pk formulalar orqali topish mumkin, bunda k € Z.

Ushbu formulalarni bittaga birlashtirish mumkin: x \u003d (-1) n p / 6 + pn, bu erda n € Z (1).

Haqiqatan ham, agar n juft son bo'lsa, ya'ni. n = 2k, keyin (1) formuladan biz x = p/6 + 2p ni olamiz va agar n toq son bo'lsa, ya'ni. n = 2k + 1, keyin (1) formuladan x = p – p/6 + 2p ni olamiz.

Javob. x \u003d (-1) n p / 6 + pn, bu erda n € Z.

sin x = -1/2 tenglamani yeching.

Yechim.

-1/2 ordinatasida M 1 va M 2 birlik doirasining ikkita nuqtasi bor, bu erda x 1 = -p/6, x 2 = -5p/6. Demak, sin x = -1/2 tenglamaning barcha ildizlarini x = -p/6 + 2pk, x = -5p/6 + 2pk, k ∈ Z formulalari orqali topish mumkin.

Biz ushbu formulalarni bittaga birlashtira olamiz: x \u003d (-1) n (-p / 6) + pn, n € Z (2).

Haqiqatan ham, agar n = 2k bo'lsa, (2) formula bo'yicha biz x = -p/6 + 2pk ni olamiz va n = 2k - 1 bo'lsa, (2) formula bo'yicha x = -5p/6 + 2pk ni topamiz.

Javob. x \u003d (-1) n (-p / 6) + pn, n € Z.

Shunday qilib, sin x = 1/2 va sin x = -1/2 tenglamalarning har biri cheksiz ko'p ildizlarga ega.

-p/2 ≤ x ≤ p/2 segmentida bu tenglamalarning har biri faqat bitta ildizga ega:
x 1 \u003d p / 6 - tenglamaning ildizi sin x \u003d 1/2 va x 1 \u003d -p / 6 - sin x \u003d -1/2 tenglamasining ildizi.

p/6 soni 1/2 sonining arksinusu deyiladi va yoziladi: arcsin 1/2 = p/6; -p/6 soni -1/2 sonining arksinusu deyiladi va ular yozadilar: arcsin (-1/2) = -p/6.

Umuman olganda, sin x \u003d a tenglamasi, bu erda -1 ≤ a ≤ 1, -p / 2 ≤ x ≤ p / 2 segmentida faqat bitta ildiz bor. Agar a ≥ 0 bo'lsa, u holda ildiz intervalga o'ralgan; agar a< 0, то в промежутке [-π/2; 0). Этот корень называют арксинусом числа а и обозначают arcsin а.

Shunday qilib, a € sonining yoyi [–1; 1] bunday raqam € [–p/2” deb ataladi; p/2], uning sinusi a.

arcsin a = a agar sin a = a va -p/2 ≤ x ≤ p/2 (3).

Masalan, arcsin √2/2 = p/4, chunki sin p/4 = √2/2 va – p/2 ≤ p/4 ≤ p/2;
arcsin (-√3/2) = -p/3, chunki sin (-p/3) = -√3/2 va – p/2 ≤ – p/3 ≤ p/2.

1 va 2 masalalarni yechishda qanday bajarilganiga o'xshab, tenglamaning ildizlari sin x = a ekanligini ko'rsatish mumkin, bu erda |a| ≤ 1 formula bilan ifodalanadi

x \u003d (-1) n arcsin a + pn, n € Z (4).

Bundan tashqari, har qanday € [-1; 1] arcsin (-a) = -arcsin a formulasi amal qiladi.

(4) formuladan tenglamaning ildizlari kelib chiqadi
a \u003d 0, a \u003d 1, a \u003d -1 uchun sin x \u003d a ni oddiyroq formulalar yordamida topish mumkin:

sin x \u003d 0 x \u003d pn, n € Z (5)

sin x \u003d 1 x \u003d p / 2 + 2pn, n € Z (6)

sin x \u003d -1 x \u003d -p / 2 + 2pn, n € Z (7)

sayt, materialni to'liq yoki qisman nusxalash bilan, manbaga havola talab qilinadi.

Eng oddiy trigonometrik tenglamalarni yechish.

Har qanday murakkablik darajasidagi trigonometrik tenglamalarni yechish oxir-oqibat eng oddiy trigonometrik tenglamalarni yechishga to‘g‘ri keladi. Va bunda trigonometrik doira yana eng yaxshi yordamchi bo'lib chiqadi.

Kosinus va sinus ta'riflarini eslang.

Burchakning kosinusu - bu birlik doiradagi nuqtaning ma'lum burchak bilan aylanishiga mos keladigan absissasi (ya'ni o'qi bo'ylab koordinatasi).

Burchakning sinusi - birlik doiradagi nuqtaning berilgan burchak bilan aylanishiga mos keladigan ordinatasi (ya'ni o'qi bo'ylab koordinatasi).

Trigonometrik doira bo'ylab harakatning ijobiy yo'nalishi soat miliga teskari harakat deb hisoblanadi. 0 daraja (yoki 0 radian) burilish koordinatalari (1; 0) bo'lgan nuqtaga to'g'ri keladi.

Biz eng oddiy trigonometrik tenglamalarni yechish uchun ushbu ta'riflardan foydalanamiz.

1. Tenglamani yeching

Bu tenglama ordinatasi ga teng bo'lgan aylananing nuqtalariga to'g'ri keladigan burilish burchagining barcha ana shunday qiymatlari bilan qanoatlantiriladi.

Y o'qida ordinatasi bo'lgan nuqtani belgilaymiz:

X o'qiga parallel gorizontal chiziqni aylana bilan kesishguncha o'tkazing. Biz aylanada yotgan va ordinataga ega bo'lgan ikkita nuqta olamiz. Bu nuqtalar burilish burchaklariga va radianlarga mos keladi:

Agar biz radianga burilish burchagiga mos keladigan nuqtani qoldirib, to'liq aylana bo'ylab aylansak, u holda biz bir radianga aylanish burchagiga mos keladigan va bir xil ordinataga ega bo'lgan nuqtaga kelamiz. Ya'ni, bu burilish burchagi ham bizning tenglamamizni qanoatlantiradi. Biz xohlagancha "bo'sh" burilishlarni amalga oshirishimiz mumkin, xuddi shu nuqtaga qaytamiz va bu burchak qiymatlarining barchasi bizning tenglamamizni qondiradi. "Bo'sh" inqiloblar soni harf (yoki) bilan belgilanadi. Biz bu inqiloblarni ham ijobiy, ham salbiy yo'nalishda qilishimiz mumkinligi sababli (yoki ) har qanday butun son qiymatlarini olishimiz mumkin.

Ya'ni, dastlabki tenglamaning birinchi qator yechimlari quyidagi ko'rinishga ega:

, , - butun sonlar to'plami (1)

Xuddi shunday, yechimlarning ikkinchi seriyasi quyidagi shaklga ega:

, Qayerda ,. (2)

Siz taxmin qilganingizdek, bu yechimlar seriyasining burilish burchagiga mos keladigan aylananing nuqtasiga asoslanadi.

Ushbu ikkita yechim seriyasini bitta yozuvga birlashtirish mumkin:

Agar biz ushbu yozuvni (ya'ni, hatto) qabul qilsak, biz yechimlarning birinchi seriyasini olamiz.

Agar biz ushbu yozuvni (ya'ni g'alati) qabul qilsak, biz ikkinchi qator echimlarni olamiz.

2. Endi tenglamani yechamiz

Birlik aylana nuqtasining abssissasi burchakdan burish natijasida olinganligi sababli, biz o'qda nuqtani abscissa bilan belgilaymiz:

Doira bilan kesishmaguncha o'qga parallel ravishda vertikal chiziq torting. Biz aylana ustida yotgan va abscissaga ega bo'lgan ikkita nuqtani olamiz. Bu nuqtalar ning aylanish burchaklariga va radianlarga mos keladi. Eslatib o'tamiz, soat yo'nalishi bo'yicha harakatlanayotganda biz salbiy burilish burchagini olamiz:

Biz ikkita yechim seriyasini yozamiz:

,

,

(Biz asosiy to'liq doiradan o'tish orqali to'g'ri nuqtaga erishamiz, ya'ni.

Keling, ushbu ikkita seriyani bitta postga birlashtiramiz:

3. Tenglamani yeching

Tangenslar chizig'i OY o'qiga parallel bo'lgan birlik doirasining koordinatalari (1,0) bo'lgan nuqtadan o'tadi.

Undagi nuqtani 1 ga teng ordinata bilan belgilang (biz burchaklari 1 bo'lgan tangensini qidiramiz):

Ushbu nuqtani koordinatali to'g'ri chiziq bilan boshlang'ich bilan bog'lang va chiziqning kesishish nuqtalarini birlik doira bilan belgilang. Chiziq va aylananing kesishish nuqtalari va ustidagi burilish burchaklariga mos keladi:

Tenglamamizni qanoatlantiradigan burilish burchaklariga mos keladigan nuqtalar bir-biridan radian masofada joylashgani uchun yechimni quyidagicha yozishimiz mumkin:

4. Tenglamani yeching

Kotangentlar chizig'i birlik doiraning koordinatalari o'qga parallel bo'lgan nuqtadan o'tadi.

Kotangentlar chizig'ida abscissa -1 bilan nuqtani belgilaymiz:

Ushbu nuqtani to'g'ri chiziqning boshiga ulang va uni aylana bilan kesishguncha davom eting. Bu chiziq aylanani aylanish burchaklari va radianlariga mos keladigan nuqtalarda kesib o'tadi:

Bu nuqtalar bir-biridan teng masofa bilan ajratilganligi sababli, bu tenglamaning umumiy yechimini quyidagicha yozishimiz mumkin:

Eng oddiy trigonometrik tenglamalarning yechimini ko'rsatuvchi misollarda trigonometrik funktsiyalarning jadval qiymatlari ishlatilgan.

Ammo, agar tenglamaning o'ng tomonida jadvaldan tashqari qiymat bo'lsa, biz tenglamaning umumiy yechimidagi qiymatni almashtiramiz:

MAXSUS ECHIMLAR:

Doiradagi ordinatasi 0 ga teng nuqtalarni belgilang:

Doira ustida ordinatasi 1 ga teng bo'lgan bitta nuqtani belgilang:

Doira ustida ordinatasi -1 ga teng bo'lgan bitta nuqtani belgilang:

Nolga yaqin qiymatlarni ko'rsatish odatiy hol bo'lgani uchun biz yechimni quyidagicha yozamiz:

Doira ustidagi nuqtalarni belgilang, ularning abtsissasi 0:

5.
Keling, aylanada abssissasi 1 ga teng bo'lgan bitta nuqtani belgilaymiz:

Aylanada abscissasi -1 ga teng bo'lgan bitta nuqtani belgilang:

Va yana bir nechta murakkab misollar:

1.

Agar argument bo'lsa, sinus bitta bo'ladi

Sinusimizning argumenti , shuning uchun biz quyidagilarni olamiz:

Tenglamaning ikkala tomonini 3 ga bo'ling:

Javob:

2.

Kosinus argumenti bo'lsa, kosinus nolga teng

Bizning kosinusimizning argumenti , shuning uchun biz olamiz:

Buning uchun biz birinchi navbatda qarama-qarshi belgi bilan o'ngga harakat qilamiz:

O'ng tomonni soddalashtiring:

Ikkala qismni -2 ga bo'ling:

E'tibor bering, atama oldidagi belgi o'zgarmaydi, chunki k har qanday butun qiymatlarni qabul qilishi mumkin.

Javob:

Xulosa qilib aytganda, "Trigonometrik aylana yordamida trigonometrik tenglamada ildizlarni tanlash" video darsini tomosha qiling.

Shu bilan eng oddiy trigonometrik tenglamalarni yechish haqidagi suhbat yakunlanadi. Keyingi safar qanday hal qilish haqida gaplashamiz.