Ahol a derékszögű háromszög megoldási feladatait vettük figyelembe, megígértem, hogy bemutatok egy technikát a szinusz és koszinusz definícióinak memorizálására. Használatával mindig gyorsan emlékezni fog, hogy melyik láb tartozik a hypotenushoz (szomszédos vagy ellentétes). Úgy döntöttem, nem halogatom a végtelenségig, a szükséges anyagokat alább találjátok, olvassátok el 😉

A tény az, hogy többször is megfigyeltem, hogy a 10-11. évfolyamos tanulók nehezen emlékeznek ezekre a meghatározásokra. Nagyon jól emlékeznek arra, hogy a láb a hypotenusára utal, de melyik- felejtsd el és zavaros. A hiba ára, amint azt a vizsgán is tudja, elvesztett pontszám.

Azoknak az információknak, amelyeket közvetlenül a matematika számára fogok bemutatni, semmi közük. Összefügg a figuratív gondolkodással, a verbális-logikai kapcsolódás módszereivel. Így van, én magam is, egyszer s mindenkorra emlékeztemdefiníciós adatok. Ha mégis elfelejti őket, akkor a bemutatott technikák segítségével mindig könnyű megjegyezni.

Hadd emlékeztesselek a szinusz és a koszinusz definícióira egy derékszögű háromszögben:

Koszinusz A derékszögű háromszög hegyesszöge a szomszédos láb és a hipotenusz aránya:

Sinus A derékszögű háromszög hegyesszöge a szemközti láb és a hipotenúzus aránya:

Szóval, milyen asszociációkat vált ki benned a koszinusz szó?

Valószínűleg mindenkinek megvan a sajátjaEmlékezz a linkre:

Így azonnal egy kifejezés lesz az emlékezetében -

«… A SZOMSZÁD láb és a hipotenúza aránya».

A koszinusz definíciójával kapcsolatos probléma megoldódott.

Ha emlékeznie kell a szinusz meghatározására egy derékszögű háromszögben, akkor a koszinusz meghatározására emlékezve könnyen megállapíthatja, hogy egy derékszögű háromszög hegyesszögének szinusza a szemközti láb és a hipotenusz aránya. Hiszen csak két láb van, ha a szomszédos szárat „foglalja” a koszinusz, akkor a szinusznak csak az ellenkező oldal marad.

Mi a helyzet az érintővel és a kotangenssel? Ugyanaz a zavar. A tanulók tudják, hogy ez a lábak aránya, de a probléma az, hogy ne feledjük, melyik melyikre utal – akár a szomszédossal szemben, akár fordítva.

Definíciók:

Tangens egy derékszögű háromszög hegyesszöge a szemközti láb és a szomszédos láb aránya:

Kotangens a hegyesszög egy derékszögű háromszögben a szomszédos láb és az ellenkező szár aránya:

Hogyan emlékezzünk? Két módja van. Az egyik verbális-logikai kapcsolatot is használ, a másik pedig matematikai kapcsolatot.

MATEMATIKAI MÓDSZER

Van egy ilyen meghatározás - az hegyesszög érintője egy szög szinuszának és koszinuszának aránya:

* Emlékezve a képletre, mindig meghatározhatja, hogy egy derékszögű háromszög hegyesszögének érintője az ellenkező láb és a szomszédos láb aránya.

Hasonlóképpen.Egy hegyesszög kotangense egy szög koszinuszának és szinuszának aránya:

Így! Ha emlékszik ezekre a képletekre, mindig megállapíthatja, hogy:

- derékszögű háromszög hegyesszögének érintője a szemközti láb és a szomszédos láb aránya

- derékszögű háromszög hegyesszögének kotangense a szomszédos láb és a szemközti szár aránya.

VERBÁLIS-LOGIKAI MÓDSZER

Az érintőről. Emlékezz a linkre:

Vagyis ha emlékeznie kell az érintő definíciójára, ezzel a logikai kapcsolattal könnyen megjegyezheti, mi az

"... az ellenkező láb és a szomszédos láb aránya"

Ha a kotangensről van szó, akkor emlékezve az érintő definíciójára, könnyen hangoztathatja a kotangens meghatározását -

"... a szomszédos láb aránya az ellenkezőjéhez"

Van egy érdekes technika a tangens és a kotangens memorizálására az oldalon " Matematikai tandem " , néz.

MÓDSZER UNIVERZÁLIS

Csak darálni lehet.De amint azt a gyakorlat mutatja, a verbális-logikai kapcsolatoknak köszönhetően az ember hosszú ideig emlékszik az információkra, és nem csak matematikai.

Remélem, hogy az anyag hasznos volt az Ön számára.

Üdvözlettel: Alexander Krutitskikh

P.S. Hálás lennék, ha a közösségi oldalakon mesélne az oldalról.

A trigonometria, mint tudomány, az ókori Keletről származik. Az első trigonometrikus arányszámokat csillagászok dolgozták ki, hogy pontos naptárt hozzanak létre és a csillagok alapján tájékozódjanak. Ezek a számítások a gömbi trigonometriára vonatkoztak, míg az iskolai kurzusban egy lapos háromszög oldalainak és szögeinek arányát vizsgálják.

A trigonometria a matematikának a trigonometrikus függvények tulajdonságaival, valamint a háromszögek oldalai és szögei közötti kapcsolatokkal foglalkozó ága.

A kultúra és a tudomány virágkorában, az i.sz. I. évezredben a tudás az ókori Keletről terjedt Görögországba. De a trigonometria fő felfedezései az arab kalifátus embereinek érdemei. Különösen a türkmén tudós, al-Marazvi olyan funkciókat vezetett be, mint az érintő és a kotangens, összeállította a szinuszok, érintők és kotangensek első értéktáblázatait. A szinusz és koszinusz fogalmát indiai tudósok vezették be. A trigonometriának nagy figyelmet szentelnek az ókor olyan nagy alakjai, mint Eukleidész, Arkhimédész és Eratoszthenész.

A trigonometria alapmennyiségei

A numerikus argumentumok alapvető trigonometrikus függvényei a szinusz, koszinusz, érintő és kotangens. Mindegyiknek megvan a saját gráfja: szinusz, koszinusz, érintő és kotangens.

Ezen mennyiségek értékének kiszámítására szolgáló képletek a Pitagorasz-tételen alapulnak. Az iskolások jobban ismerik a megfogalmazásban: „Pitagorasz nadrág, minden irányban egyenlő”, mivel a bizonyítékot egy egyenlő szárú derékszögű háromszög példáján adjuk meg.

Szinusz, koszinusz és más függőségek kapcsolatot létesítenek bármely derékszögű háromszög hegyesszögei és oldalai között. Képleteket adunk ezeknek a mennyiségeknek az A szögre történő kiszámításához, és nyomon követjük a trigonometrikus függvények kapcsolatát:

Mint látható, a tg és a ctg inverz függvények. Ha az a lábat a sin A és a c hipotenusz szorzataként, a b lábat pedig cos A * cként ábrázoljuk, akkor a következő képleteket kapjuk az érintőre és a kotangensre:

trigonometrikus kör

Grafikusan az említett mennyiségek aránya a következőképpen ábrázolható:

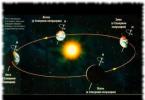
A kör ebben az esetben az α szög összes lehetséges értékét képviseli 0°-tól 360°-ig. Amint az ábrán látható, minden függvény a szögtől függően negatív vagy pozitív értéket vesz fel. Például a sin α „+” jelű lesz, ha α a kör I és II negyedéhez tartozik, azaz 0 ° és 180 ° közötti tartományban van. 180° és 360° közötti α (III. és IV. negyed) esetén a sin α csak negatív érték lehet.

Próbáljunk meg trigonometrikus táblázatokat készíteni adott szögekhez, és megtudjuk a mennyiségek jelentését.

A 30°, 45°, 60°, 90°, 180° és így tovább α értékeit speciális eseteknek nevezzük. A trigonometrikus függvények értékeit kiszámítják és speciális táblázatok formájában mutatják be.

Ezeket a szögeket nem véletlenül választották ki. A táblázatokban a π jelölés a radiánokra vonatkozik. Rad az a szög, amelyben a körív hossza megfelel a sugarának. Ezt az értéket egy univerzális összefüggés megállapítása érdekében vezették be, radiánban történő számításnál a sugár cm-ben megadott tényleges hossza nem számít.

A trigonometrikus függvények táblázatában szereplő szögek radiánértékeknek felelnek meg:

Tehát nem nehéz kitalálni, hogy 2π egy teljes kör vagy 360°.

A trigonometrikus függvények tulajdonságai: szinusz és koszinusz

A szinusz és koszinusz, érintő és kotangens alapvető tulajdonságainak figyelembe vételéhez és összehasonlításához szükséges ezek függvényeinek felrajzolása. Ez megtehető egy kétdimenziós koordináta-rendszerben elhelyezett görbe formájában.

Tekintsünk egy összehasonlító táblázatot a szinuszhullám és a koszinuszhullám tulajdonságairól:

szinuszos	koszinusz hullám
y = sin x	y = cos x
ODZ [-1; 1]	ODZ [-1; 1]
sin x = 0, ha x = πk, ahol k ϵ Z	cos x = 0, ha x = π/2 + πk, ahol k ϵ Z
sin x = 1, ha x = π/2 + 2πk, ahol k ϵ Z	cos x = 1, ha x = 2πk, ahol k ϵ Z
sin x = - 1, ahol x = 3π/2 + 2πk, ahol k ϵ Z	cos x = - 1, ha x = π + 2πk, ahol k ϵ Z
sin (-x) = - sin x, azaz páratlan függvény	cos (-x) = cos x, azaz a függvény páros
	a függvény periodikus, a legkisebb periódus 2π
sin x › 0, ahol x az I. és II. negyedhez tartozik, vagy 0°-tól 180°-ig (2πk, π + 2πk)	cos x › 0, ahol x az I. és IV. negyedhez tartozik, vagy 270°-tól 90°-ig (- π/2 + 2πk, π/2 + 2πk)
sin x ‹ 0, ahol x a III. és IV. negyedhez tartozik, vagy 180°-tól 360°-ig (π + 2πk, 2π + 2πk)	cos x ‹ 0, ahol x a II. és III. negyedhez tartozik, vagy 90°-tól 270°-ig (π/2 + 2πk, 3π/2 + 2πk)
növekszik a [- π/2 + 2πk, π/2 + 2πk] intervallumon	növekszik a [-π + 2πk, 2πk] intervallumon
csökken a [ π/2 + 2πk, 3π/2 + 2πk] intervallumokon	időközönként csökken
derivált (sin x)' = cos x	derivált (cos x)’ = - sin x

Annak meghatározása, hogy egy függvény páros-e vagy sem, nagyon egyszerű. Elég elképzelni egy trigonometrikus kört trigonometrikus mennyiségek jeleivel, és gondolatban „hajtogatni” a grafikont az OX tengelyéhez képest. Ha az előjelek megegyeznek, a függvény páros, ellenkező esetben pedig páratlan.

A radiánok bevezetése, valamint a szinuszos és koszinuszhullám főbb tulajdonságainak felsorolása lehetővé teszi a következő mintát:

Nagyon könnyű ellenőrizni a képlet helyességét. Például x = π/2 esetén a szinusz egyenlő 1-gyel, csakúgy, mint az x = 0 koszinusza. Az ellenőrzés elvégezhető táblázatok megtekintésével vagy adott értékek függvénygörbéinek nyomon követésével.

A tangentoid és a kotangentoid tulajdonságai

Az érintő és a kotangens függvények grafikonjai jelentősen eltérnek a szinuszos és koszinuszos hullámtól. A tg és ctg értékek fordítottak egymással.

1. Y = tgx.
2. Az érintő az x = π/2 + πk y értékei felé hajlik, de soha nem éri el azokat.
3. A tangentoid legkisebb pozitív periódusa π.
4. Tg (- x) \u003d - tg x, azaz a függvény páratlan.
5. Tg x = 0, ha x = πk.
6. A funkció növekszik.
7. Tg x › 0, x ϵ esetén (πk, π/2 + πk).
8. Tg x ‹ 0, x ϵ esetén (— π/2 + πk, πk).
9. Derivált (tg x)' = 1/cos 2⁡x .

Tekintsük a kotangentoid grafikus ábrázolását az alábbiakban a szövegben.

A kotangentoid fő tulajdonságai:

1. Y = ctgx.
2. A szinusz- és koszinuszfüggvényekkel ellentétben a tangentoidban Y felveheti az összes valós szám halmazának értékét.
3. A kotangentoid az x = πk y értékei felé hajlik, de soha nem éri el azokat.
4. A kotangentoid legkisebb pozitív periódusa π.
5. Ctg (- x) \u003d - ctg x, azaz a függvény páratlan.
6. Ctg x = 0, ha x = π/2 + πk.
7. A funkció csökken.
8. Ctg x › 0, x ϵ esetén (πk, π/2 + πk).
9. Ctg x ‹ 0, x ϵ esetén (π/2 + πk, πk).
10. Származék (ctg x)' = - 1/sin 2 ⁡x Fix

A trigonometrikus függvények értéktáblázata

jegyzet. Ez a trigonometrikus függvények értéktáblázata a √ jelet használja a négyzetgyök jelölésére. A tört jelölésére - a "/" szimbólum.

Lásd még hasznos anyagok:

Mert trigonometrikus függvény értékének meghatározása, keresse meg a trigonometrikus függvényt jelző egyenes metszéspontjában. Például egy 30 fokos szinusz - keresünk egy oszlopot a sin (szinusz) fejléccel, és megtaláljuk a táblázat ezen oszlopának metszéspontját a "30 fokos" vonallal, a metszéspontjuknál olvassuk az eredményt - egy második. Hasonlóképpen találjuk koszinusz 60 fokok, szinusz 60 fokok (még egyszer a sin (szinusz) oszlop és a 60 fokos sor metszéspontjában találjuk a sin 60 = √3/2 értéket, stb. Ugyanígy megtalálhatók más "népszerű" szögek szinuszainak, koszinuszainak és érintőinek értékei is.

Pi szinusza, pi koszinusza, pi tangense és egyéb szögek radiánban

Az alábbi koszinuszokat, szinuszokat és érintőket tartalmazó táblázat alkalmas olyan trigonometrikus függvények értékének meghatározására is, amelyek argumentuma radiánban megadva. Ehhez használja a szögértékek második oszlopát. Ennek köszönhetően átválthatja a népszerű szögek értékét fokról radiánra. Például keressük meg az első sorban a 60 fokos szöget, és olvassuk le alatta az értékét radiánban. 60 fok egyenlő π/3 radiánnal.

A pi szám egyértelműen kifejezi a kör kerületének a szög mértékétől való függését. Tehát a pi radián 180 fokkal egyenlő.

Bármely pi-ben (radiánban) kifejezett szám könnyen átváltható fokokká, ha a pi (π) számot 180-ra cseréljük..

Példák:
1. sine pi.
sin π = sin 180 = 0
így a pi szinusza megegyezik a 180 fokos szinuszával, és egyenlő nullával.

2. koszinusz pi.
cos π = cos 180 = -1
így a pi koszinusza megegyezik 180 fokos koszinuszával, és egyenlő mínusz eggyel.

3. Érintő pi
tg π = tg 180 = 0
így a pi érintője megegyezik a 180 fokos érintővel, és egyenlő nullával.

Szinusz, koszinusz, érintő értékek táblázata 0 - 360 fokos szögekhez (gyakori értékek)

α szög (fok)	α szög radiánban (a pi-n keresztül)	bűn (sinus)	kötözősaláta (koszinusz)	tg (tangens)	ctg (kotangens)	mp (metsző)	ok (koszekáns)
0	0	0	1	0	-	1	-
15	π/12			2 - √3	2 + √3
30	π/6	1/2	√3/2	1/√3	√3	2/√3	2
45	π/4	√2/2	√2/2	1	1	√2	√2
60	π/3	√3/2	1/2	√3	1/√3	2	2/√3
75	5π/12			2 + √3	2 - √3
90	π/2	1	0	-	0	-	1
105	7π/12		-	- 2 - √3	√3 - 2
120	2π/3	√3/2	-1/2	-√3	-√3/3
135	3π/4	√2/2	-√2/2	-1	-1	-√2	√2
150	5π/6	1/2	-√3/2	-√3/3	-√3
180	π	0	-1	0	-	-1	-
210	7π/6	-1/2	-√3/2	√3/3	√3
240	4π/3	-√3/2	-1/2	√3	√3/3
270	3π/2	-1	0	-	0	-	-1
360	2π	0	1	0	-	1	-

Ha a trigonometrikus függvények értéktáblázatában a függvény értéke helyett kötőjel van feltüntetve (tangens (tg) 90 fok, kotangens (ctg) 180 fok), akkor adott értéknél a fokmérő a szög, a függvénynek nincs határozott értéke. Ha nincs kötőjel, akkor a cella üres, tehát még nem adtuk meg a kívánt értéket. Érdekel bennünket, hogy a felhasználók milyen kérésekre fordulnak hozzánk, és új értékekkel egészítjük ki a táblázatot, annak ellenére, hogy a leggyakrabban előforduló szögértékek koszinuszainak, szinuszainak és érintőinek aktuális adatai elegendőek a legtöbb megoldáshoz. problémákat.

A sin, cos, tg trigonometrikus függvények értéktáblázata a legnépszerűbb szögekhez
0, 15, 30, 45, 60, 90 ... 360 fok
(numerikus értékek "a Bradis táblázatok szerint")

szögérték α (fok)	α szög értéke radiánban	bűn (szinusz)	cos (koszinusz)	tg (érintő)	ctg (kotangens)
0	0
15		0,2588	0,9659	0,2679
30		0,5000		0,5774
45		0,7071
		0,7660
60		0,8660	0,5000	1,7321
	7π/18

A szinusz, koszinusz, érintő és kotangens fogalma a trigonometria - a matematika egyik ága - fő kategóriái, és elválaszthatatlanul kapcsolódnak a szög meghatározásához. Ennek a matematikai tudománynak a birtoklása megköveteli a képletek és tételek memorizálását és megértését, valamint fejlett térbeli gondolkodást. Éppen ezért a trigonometrikus számítások gyakran nehézségeket okoznak az iskolásoknak és a diákoknak. Ezek leküzdéséhez jobban meg kell ismerkednie a trigonometrikus függvényekkel és képletekkel.

Fogalmak a trigonometriában

A trigonometria alapfogalmainak megértéséhez először el kell döntenie, hogy mi a derékszögű háromszög és egy kör szöge, és miért van hozzájuk társítva minden alapvető trigonometrikus számítás. Az a háromszög, amelyben az egyik szög 90 fokos, derékszögű. Történelmileg ezt a figurát gyakran használták az építészetben, a navigációban, a művészetben, a csillagászatban. Ennek megfelelően az ábra tulajdonságait tanulmányozva és elemezve az emberek a paraméterek megfelelő arányának kiszámításához jutottak.

A derékszögű háromszögekhez kapcsolódó fő kategóriák a hipotenusz és a lábak. A hipotenusz egy háromszögnek a derékszöggel ellentétes oldala. A lábak a másik két oldal. Bármely háromszög szögeinek összege mindig 180 fok.

A gömbi trigonometria a trigonometria olyan része, amelyet az iskolában nem tanulnak, de az alkalmazott tudományokban, például a csillagászatban és a geodéziában használják a tudósok. A gömbi trigonometriában a háromszög jellemzője, hogy szögeinek összege mindig nagyobb, mint 180 fok.

Egy háromszög szögei

Egy derékszögű háromszögben egy szög szinusza a kívánt szöggel ellentétes szár és a háromszög befogójának aránya. Ennek megfelelően a koszinusz a szomszédos láb és a hypotenus aránya. Mindkét érték mindig kisebb egynél, mivel a hipotenusz mindig hosszabb, mint a láb.

A szög érintője egy olyan érték, amely megegyezik a kívánt szög szemközti szárának a szomszédos szárhoz viszonyított arányával, vagy szinusz és koszinusz. A kotangens pedig a kívánt szögű szomszédos láb és az ellenkező kaktett aránya. Egy szög kotangensét úgy is megkaphatjuk, hogy az egységet elosztjuk az érintő értékével.

egységkör

Az egységkör a geometriában olyan kör, amelynek sugara eggyel egyenlő. Egy ilyen kört a derékszögű koordinátarendszerben szerkesztünk úgy, hogy a kör középpontja egybeesik a kezdőponttal, és a sugárvektor kezdeti helyzetét az X tengely (abszcissza tengely) pozitív iránya határozza meg. A kör minden pontjának két koordinátája van: XX és YY, vagyis az abszcissza és az ordináta koordinátái. A kör XX síkban tetszőleges pontját kiválasztva, és onnan a merőlegest az abszcissza tengelyre ejtve a kiválasztott pontra egy sugárral alkotott derékszögű háromszöget kapunk (jelöljük C betűvel), egy merőlegest az X tengely (a metszéspontot G betű jelöli), és egy szakasz az abszcissza tengely az origó (a pontot A betűvel jelöljük) és a G metszéspont között. Az így kapott ACG háromszög egy derékszögű háromszög egy kör, ahol AG a hipotenusz, AC és GC pedig a lábak. Az AC kör sugara és az abszcissza tengely AG jelölésű szakasza közötti szöget α-nak (alfa) definiáljuk. Tehát cos α = AG/AC. Tekintettel arra, hogy AC az egységkör sugara, és egyenlő eggyel, kiderül, hogy cos α=AG. Hasonlóképpen, sin α=CG.

Ezen kívül ezen adatok ismeretében meg lehet határozni a kör C pontjának koordinátáját, hiszen cos α=AG, és sin α=CG, ami azt jelenti, hogy a C pontnak megvannak a megadott koordinátái (cos α; sin α). Tudva, hogy az érintő egyenlő a szinusz és a koszinusz arányával, megállapíthatjuk, hogy tg α \u003d y / x és ctg α \u003d x / y. Negatív koordinátarendszerben a szögeket figyelembe véve kiszámítható, hogy egyes szögek szinusz és koszinusz értéke negatív is lehet.

Számítások és alapképletek

A trigonometrikus függvények értékei

Ha figyelembe vesszük a trigonometrikus függvények lényegét az egységkörön keresztül, néhány szögre levezethetjük ezeknek a függvényeknek az értékeit. Az értékeket az alábbi táblázat tartalmazza.

A legegyszerűbb trigonometrikus azonosságok

Azokat az egyenleteket, amelyekben a trigonometrikus függvény előjele alatt ismeretlen érték található, trigonometrikusnak nevezzük. A sin x = α értékű azonosságok, k tetszőleges egész szám:

1. sin x = 0, x = πk.
2. 2. sin x \u003d 1, x \u003d π / 2 + 2πk.
3. sin x \u003d -1, x \u003d -π / 2 + 2πk.
4. sin x = a, |a| > 1, nincs megoldás.
5. sin x = a, |a| ≦ 1, x = (-1)^k * arcsin α + πk.

A cos x = a értékű azonosságok, ahol k tetszőleges egész szám:

1. cos x = 0, x = π/2 + πk.
2. cos x = 1, x = 2πk.
3. cos x \u003d -1, x \u003d π + 2πk.
4. cos x = a, |a| > 1, nincs megoldás.
5. cos x = a, |a| ≦ 1, х = ±arccos α + 2πk.

A tg x = a értékű azonosságok, ahol k tetszőleges egész szám:

1. tg x = 0, x = π/2 + πk.
2. tg x \u003d a, x \u003d arctg α + πk.

Ctg x = a értékű azonosságok, ahol k tetszőleges egész szám:

1. ctg x = 0, x = π/2 + πk.
2. ctg x \u003d a, x \u003d arcctg α + πk.

Öntött képletek

A konstans képletek e kategóriája olyan módszereket jelöl, amelyek segítségével az alak trigonometrikus függvényeitől az argumentum függvényeihez lehet lépni, azaz bármely értékű szög szinuszát, koszinuszát, tangensét és kotangensét át lehet alakítani a szög megfelelő mutatóira. a 0 és 90 fok közötti intervallum a számítások kényelmesebbé tétele érdekében.

A szög szinuszának redukciós függvényei így néznek ki:

• sin(900 - α) = α;
• sin(900 + α) = cos α;
• sin(1800 - α) = sin α;
• sin(1800 + α) = -sin α;
• sin(2700 - α) = -cos α;
• sin(2700 + α) = -cos α;
• sin(3600 - α) = -sin α;
• sin(3600 + α) = sin α.

Egy szög koszinuszához:

• cos(900 - α) = sin α;
• cos(900 + α) = -sin α;
• cos(1800 - α) = -cos α;
• cos(1800 + α) = -cos α;
• cos(2700 - α) = -sin α;
• cos(2700 + α) = sin α;
• cos(3600 - α) = cos α;
• cos(3600 + α) = cos α.

A fenti képletek használata két szabály szerint lehetséges. Először is, ha a szög értékként (π/2 ± a) vagy (3π/2 ± a) ábrázolható, a függvény értéke megváltozik:

• bűnből cos-ba;
• cos-ból bűnbe;
• tg-ről ctg-re;
• ctg-től tg-ig.

A függvény értéke változatlan marad, ha a szög ábrázolható (π ± a) vagy (2π ± a).

Másodszor, a redukált függvény előjele nem változik: ha kezdetben pozitív volt, akkor az is marad. Ugyanez igaz a negatív függvényekre is.

Összeadási képletek

Ezek a képletek két forgási szög összegének és különbségének szinuszának, koszinuszának, érintőjének és kotangensének az értékeit fejezik ki trigonometrikus függvényeikben. A szögeket általában α-val és β-val jelölik.

A képletek így néznek ki:

1. sin(α ± β) = sin α * cos β ± cos α * sin.
2. cos(α ± β) = cos α * cos β ∓ sin α * sin.
3. tan(α ± β) = (tan α ± tan β) / (1 ∓ tan α * tan β).
4. ctg(α ± β) = (-1 ± ctg α * ctg β) / (ctg α ± ctg β).

Ezek a képletek bármely α és β szögre érvényesek.

Dupla és hármas szög képletek

A kettős és hármas szög trigonometrikus képlete olyan képlet, amely a 2α és 3α szögek függvényét az α szög trigonometrikus függvényeihez viszonyítja. Összeadási képletekből származik:

1. sin2α = 2sinα*cosα.
2. cos2α = 1 - 2sin^2α.
3. tg2α = 2tgα / (1 - tg^2 α).
4. sin3α = 3sinα - 4sin^3α.
5. cos3α = 4cos^3α - 3cosα.
6. tg3α = (3tgα - tg^3α) / (1-tg^2α).

Átmenet az összegről a termékre

Figyelembe véve, hogy 2sinx*cosy = sin(x+y) + sin(x-y), leegyszerűsítve ezt a képletet, a sinα + sinβ = 2sin(α + β)/2 * cos(α − β)/2 azonosságot kapjuk. Hasonlóképpen, sinα - sinβ = 2sin(α - β)/2 * cos(α + β)/2; cosα + cosβ = 2cos(α + β)/2 * cos(α − β)/2; cosα - cosβ = 2sin(α + β)/2 * sin(α − β)/2; tgα + tgβ = sin(α + β) / cosα * cosβ; tgα - tgβ = sin(α - β) / cosα * cosβ; cosα + sinα = √2sin(π/4 ∓ α) = √2cos(π/4 ± α).

Átmenet a termékről az összegre

Ezek a képletek az összeg és a szorzat közötti átmenet azonosságaiból következnek:

• sinα * sinβ = 1/2*;
• cosα * cosβ = 1/2*;
• sinα * cosβ = 1/2*.

Redukciós képletek

Ezekben az azonosságokban a szinusz és koszinusz négyzet- és köbhatványai a többszörös szög első hatványának szinuszával és koszinuszával fejezhetők ki:

• sin^2 α = (1 - cos2α)/2;
• cos^2α = (1 + cos2α)/2;
• sin^3 α = (3 * sinα - sin3α)/4;
• cos^3 α = (3 * cosα + cos3α)/4;
• sin^4 α = (3 - 4cos2α + cos4α)/8;
• cos^4 α = (3 + 4cos2α + cos4α)/8.

Univerzális helyettesítés

Az univerzális trigonometrikus helyettesítési képletek a trigonometrikus függvényeket a félszög érintőjével fejezik ki.

• sin x \u003d (2tgx / 2) * (1 + tg ^ 2 x / 2), míg x \u003d π + 2πn;
• cos x = (1 - tg^2 x/2) / (1 + tg^2 x/2), ahol x = π + 2πn;
• tg x \u003d (2tgx / 2) / (1 - tg ^ 2 x / 2), ahol x \u003d π + 2πn;
• ctg x \u003d (1 - tg ^ 2 x / 2) / (2tgx / 2), míg x \u003d π + 2πn.

Különleges esetek

Az alábbiakban a legegyszerűbb trigonometrikus egyenletek speciális eseteit mutatjuk be (k bármely egész szám).

Privát szinusz:

sin x érték	x érték
0	pk
1	π/2 + 2πk
-1	-π/2 + 2πk
1/2	π/6 + 2πk vagy 5π/6 + 2πk
-1/2	-π/6 + 2πk vagy -5π/6 + 2πk
√2/2	π/4 + 2πk vagy 3π/4 + 2πk
-√2/2	-π/4 + 2πk vagy -3π/4 + 2πk
√3/2	π/3 + 2πk vagy 2π/3 + 2πk
-√3/2	-π/3 + 2πk vagy -2π/3 + 2πk

Koszinusz hányadosok:

cos x érték	x érték
0	π/2 + 2πk
1	2πk
-1	2 + 2πk
1/2	±π/3 + 2πk
-1/2	±2π/3 + 2πk
√2/2	±π/4 + 2πk
-√2/2	±3π/4 + 2πk
√3/2	±π/6 + 2πk
-√3/2	±5π/6 + 2πk

Magán az érintőhöz:

tg x érték	x érték
0	pk
1	π/4 + πk
-1	-π/4 + πk
√3/3	π/6 + πk
-√3/3	-π/6 + πk
√3	π/3 + πk
-√3	-π/3 + πk

Kotangens hányadosok:

ctg x érték	x érték
0	π/2 + πk
1	π/4 + πk
-1	-π/4 + πk
√3	π/6 + πk
-√3	-π/3 + πk
√3/3	π/3 + πk
-√3/3	-π/3 + πk

Tételek

Szinusztétel

A tételnek két változata van - egyszerű és kiterjesztett. Egyszerű szinusztétel: a/sin α = b/sin β = c/sin γ. Ebben az esetben a, b, c a háromszög oldalai, α, β, γ pedig a szemközti szögek.

Kiterjesztett szinusztétel tetszőleges háromszögre: a/sin α = b/sin β = c/sin γ = 2R. Ebben az azonosságban R jelöli annak a körnek a sugarát, amelybe az adott háromszög be van írva.

Koszinusz tétel

Az azonosság a következőképpen jelenik meg: a^2 = b^2 + c^2 - 2*b*c*cos α. A képletben a, b, c a háromszög oldalai, α pedig az a-val szemközti szög.

Érintőtétel

A képlet két szög érintőinek és a velük szemben lévő oldalak hosszának az összefüggését fejezi ki. Az oldalak a, b, c jelzéssel vannak ellátva, a megfelelő szemközti szögek pedig α, β, γ. Az érintőtétel képlete: (a - b) / (a+b) = tg((α - β)/2) / tg((α + β)/2).

Kotangens tétel

A háromszögbe írt kör sugarát az oldalainak hosszához társítja. Ha a, b, c egy háromszög oldalai, és A, B, C ezek ellentétes szögei, r a beírt kör sugara, p pedig a háromszög fél kerülete, a következő azonosságok tart:

• ctg A/2 = (p-a)/r;
• ctg B/2 = (p-b)/r;
• ctg C/2 = (p-c)/r.

Alkalmazások

A trigonometria nemcsak matematikai képletekhez kapcsolódó elméleti tudomány. Tulajdonságait, tételeit és szabályait az emberi tevékenység különböző ágai a gyakorlatban használják - csillagászat, légi és tengeri navigáció, zeneelmélet, geodézia, kémia, akusztika, optika, elektronika, építészet, közgazdaságtan, gépészet, mérési munka, számítógépes grafika, térképészet, óceánográfia és még sok más.

A szinusz, a koszinusz, az érintő és a kotangens a trigonometria alapfogalmai, amelyekkel matematikailag kifejezhető a háromszög szögei és oldalhosszai közötti kapcsolat, és azonosságokon, tételeken és szabályokon keresztül megtalálhatja a kívánt mennyiségeket.

A trigonometria alapképletei olyan képletek, amelyek kapcsolatot teremtenek az alapvető trigonometrikus függvények között. A szinusz, a koszinusz, az érintő és a kotangens számos kapcsolaton keresztül kapcsolódnak egymáshoz. Az alábbiakban megadjuk a fő trigonometrikus képleteket, és a kényelem kedvéért céljuk szerint csoportosítjuk őket. Ezekkel a képletekkel szinte bármilyen problémát megoldhat a standard trigonometria tanfolyamból. Azonnal megjegyezzük, hogy az alábbiakban csak magukat a képleteket adjuk meg, és nem azok származtatását, amelyeknek külön cikkeket szentelünk.

A trigonometria alapvető azonosságai

A trigonometrikus azonosságok összefüggést adnak egy szög szinusza, koszinusza, érintője és kotangense között, lehetővé téve, hogy egy függvényt egy másikkal fejezzünk ki.

Trigonometrikus azonosságok

sin 2 a + cos 2 a = 1 t g α = sin α cos α , c t g α = cos α sin α t g α c t g α = 1 t g 2 α + 1 = 1 cos 2 α , c t g 2 α 1

Ezek az azonosságok közvetlenül következnek az egységkör, a szinusz (sin), koszinusz (cos), érintő (tg) és kotangens (ctg) definícióiból.

Öntött képletek

Az öntési képletek lehetővé teszik, hogy a tetszőleges és tetszőlegesen nagy szögekkel való munkavégzésről a 0 és 90 fok közötti szögek közötti munkavégzésre váltson.

Öntött képletek

sin α + 2 π z = sin α , cos α + 2 π z = cos α t g α + 2 π z = t g α , c t g α + 2 π z = c t g α sin - α + = - 2 π z cos - α + 2 π z = cos α t g - α + 2 π z = - t g α , c t g - α + 2 π z = - c t g α sin π 2 + α + 2 π z = cos α , cos π 2 + α + 2 π z = - sin α t g π 2 + α + 2 π z = - c t g α , c t g π 2 + α + 2 π z = - t g α sin π 2 - α + 2 π z =, cos π z π 2 - α + 2 π z = sin α t g π 2 - α + 2 π z = c t g α , c t g π 2 - α + 2 π z = t g α sin π + α + 2 π z = -s π z π + α + 2 π z = - cos α t g π + α + 2 π z = t g α , c t g π + α + 2 π z = c t g α sin π - α + 2 π z + 2 π z = - cos α t g π - α + 2 π z = - t g α , c t g π - α + 2 π z = - c t g α sin 3 π 2 + α + 2 π z =, cos 3 π 2 + α + 2 π z = sin α t g 3 π 2 + α + 2 π z = - c t g α , c t g 3 π 2 + α + 2 π z = - t g α sin 3 π 2 π = - cos α , cos 3 π 2 - α + 2 π z = - sin α t g 3 π 2 - α + 2 π z = c t g α , c t g 3 π 2 - α + 2 π z = t g α

A redukciós képletek a trigonometrikus függvények periodicitásának következményei.

Trigonometrikus összeadási képletek

A trigonometria összeadási képletei lehetővé teszik a szögek összegének vagy különbségének trigonometrikus függvényének kifejezését e szögek trigonometrikus függvényében.

Trigonometrikus összeadási képletek

sin α ± β = sin α cos β ± cos α sin β cos α + β = cos α cos β - sin α sin β cos α - β = cos α cos β + sin α sin β t g α ± ± g α t t g β 1 ± t g α t g β c t g α ± β = - 1 ± c t g α c t g β c t g α ± c t g β

Az összeadási képletek alapján a többszörös szög trigonometrikus képletei származnak.

Több szögképletek: dupla, hármas stb.

Dupla és hármas szög képletek

sin 2 α \u003d 2 sin α cos α cos 2 α \u003d cos 2 α - sin 2 α, cos 2 α \u003d 1 - 2 sin 2 α, cos 2 α \u003d α \u003d α 2 cos u003d 2 t g α 1 - t g 2 α t g 2 α mellett \u003d t g 2 α - 1 2 t g α sin 3 α \u003d 3 sin α cos 2 α - sin 3 α 3 α, sinu 3 α 3 4 sin 3 α cos 3 α = cos 3 α - 3 sin 2 α cos α , cos 3 α = - 3 cos α + 4 cos 3 α t g 3 α = 3 t g α - t g 3 α gt gt 1 - 23 3 α = c t g 3 α - 3 c t g α 3 c t g 2 α - 1

Félszög képletek

A trigonometriai félszög-képletek a kettősszög-képletek következményei, és a félszög alapfüggvényei és a teljes szög koszinusza közötti kapcsolatot fejezik ki.

Félszög képletek

sin 2 α 2 = 1 - cos α 2 cos 2 α 2 = 1 + cos α 2 t g 2 α 2 = 1 - cos α 1 + cos α c t g 2 α 2 = 1 + cos α 1 - cos α

Redukciós képletek

Redukciós képletek

sin 2 α = 1 - cos 2 α 2 cos 2 α = 1 + cos 2 α 2 sin 3 α = 3 sin α - sin 3 α 4 cos 3 α = 3 cos α + cos 3 α 4 sin 4 α = 3 - 4 cos 2 α + cos 4 α 8 cos 4 α = 3 + 4 cos 2 α + cos 4 α 8

A számítások során gyakran kényelmetlen nehézkes erőkkel dolgozni. A fokcsökkentési képletek lehetővé teszik a trigonometrikus függvény mértékének csökkentését tetszőleges nagyról az elsőre. Íme az általános véleményük:

A redukciós képletek általános formája

mert még n

sin n α = C n 2 n 2 n + 1 2 n - 1 ∑ k = 0 n 2 - 1 (- 1) n 2 - k C k n cos ((n - 2 k) α) cos n α = C n 2 n 2 n + 1 2 n - 1 ∑ k = 0 n 2 - 1 C k n cos ((n - 2 k) α)

páratlan n

sin n α = 1 2 n - 1 ∑ k = 0 n - 1 2 (- 1) n - 1 2 - k C k n sin ((n - 2 k) α) cos n α = 1 2 n - 1 ∑ k = 0 n - 1 2 C k n cos ((n - 2 k) α)

Trigonometrikus függvények összege és különbsége

A trigonometrikus függvények különbsége és összege szorzatként ábrázolható. A szinuszok és koszinuszok különbségeinek faktorálása nagyon kényelmesen használható trigonometrikus egyenletek megoldásához és kifejezések egyszerűsítéséhez.

Trigonometrikus függvények összege és különbsége

sin α + sin β = 2 sin α + β 2 cos α - β 2 sin α - sin β = 2 sin α - β 2 cos α + β 2 cos α + cos β = 2 cos α + β 2 β cos α - 2 cos α - cos β \u003d - 2 sin α + β 2 sin α - β 2, cos α - cos β \u003d 2 sin α + β 2 sin β - α 2

Trigonometrikus függvények szorzata

Ha a függvények összegének és különbségének képlete lehetővé teszi, hogy a szorzatukra lépjen, akkor a trigonometrikus függvények szorzatának képletei fordított átmenetet hajtanak végre - a szorzatról az összegre. A szinuszok, koszinuszok és szinuszos koszinuszok szorzatának képleteit figyelembe veszik.

Képletek trigonometrikus függvények szorzatára

sin α sin β = 1 2 (cos (α - β) - cos (α + β)) cos α cos β = 1 2 (cos (α - β) + cos (α + β)) sin α cos β = 1 2 (sin (α - β) + sin (α + β))

Univerzális trigonometrikus helyettesítés

Minden alapvető trigonometrikus függvény - szinusz, koszinusz, érintő és kotangens - kifejezhető a félszög érintőjével.

Univerzális trigonometrikus helyettesítés

sin α = 2 t g α 2 1 + t g 2 α 2 cos α = 1 - t g 2 α 2 1 + t g 2 α 2 t g α = 2 t g α 2 1 - t g 2 α 2 g = 2 t 1 α 2 2 t g α 2

Ha hibát észlel a szövegben, jelölje ki, és nyomja meg a Ctrl+Enter billentyűkombinációt