Az óra céljai:

• nevelési: homogén egyenletet tartalmazó egyenletrendszerek, szimmetrikus egyenletrendszerek megoldásának megtanulása;
• fejlesztés: a gondolkodás, a figyelem, a memória fejlesztése, a fő dolog kiemelésének képessége;
• nevelési: kommunikációs készségek fejlesztése.

Az óra típusa: lecke új anyag tanulása.

Használt tanulási technológiák:

• csoportokban dolgoznak;
• tervezési módszer.

Felszerelés: számítógép, multimédiás projektor.

Egy héttel az óra előtt a diákok kreatív feladatokhoz kapnak témákat (lehetőségek szerint).
I lehetőség. Szimmetrikus egyenletrendszerek. Megoldások.
II lehetőség. Homogén egyenletet tartalmazó rendszerek. Megoldások.

Minden tanulónak további oktatási irodalom felhasználásával meg kell találnia a megfelelő oktatási anyagot, ki kell választania egy egyenletrendszert és meg kell oldania.
Mindegyik lehetőségből egy diák multimédiás prezentációt készít a kreatív feladat témájában. A tanár szükség szerint útmutatást ad a tanulóknak.

I. A tanulók tanulási tevékenységének motivációja

A tanár bevezető beszéde
Az előző leckében egyenletrendszerek megoldását vizsgáltuk az ismeretlenek helyettesítésének módszerével. Nincs általános szabály az új változók kiválasztására. Azonban kétféle egyenletrendszert lehet megkülönböztetni, ha van ésszerű változóválasztás:

• szimmetrikus egyenletrendszerek;
• egyenletrendszerek, amelyek közül az egyik homogén.

II. Új anyagok tanulása

A második lehetőség tanulói beszámolnak házi feladatukról.

1. "Homogén egyenletet tartalmazó rendszerek" multimédiás bemutató diavetítése (1. prezentáció).

2. Egy asztalnál ülő tanulópáros munka: a második lehetőség tanulója elmagyarázza az asztal szomszédjának egy homogén egyenletet tartalmazó rendszer megoldását.

Az 1. lehetőség tanulóinak beszámolója.

1. A "Szimmetrikus egyenletrendszerek" multimédiás bemutató diavetítése (2. prezentáció).

A tanulók a füzetükbe írják:

2. Egy asztalnál ülő tanulópáros munka: az I. lehetőség tanulója elmagyarázza az asztal szomszédjának egy szimmetrikus egyenletrendszer megoldását.

III. A tanult anyag konszolidációja

Csoportos munkavégzés (egy 4 fős csoportban a szomszédos asztaloknál ülő tanulókat egyesítjük).
A 6 csoport mindegyike elvégzi a következő feladatot.

Határozza meg a rendszer típusát és oldja meg:

A tanulók csoportosan elemzik a rendszereket, meghatározzák azok típusát, majd a frontális munka során megbeszélik a rendszerek megoldásait.

rendszer

szimmetrikus, új változókat vezetünk be x+y=u, xy=v

b) rendszer

homogén egyenletet tartalmaz.

A számpár (0;0) nem megoldása a rendszernek.

IV. A tanulók tudásának ellenőrzése

Önálló munka az opciókon.

Oldja meg az egyenletrendszert:

A tanulók áttekintésre leadják füzeteiket a tanárnak.

V. Házi feladat

1. Minden tanuló előadja.

Oldja meg az egyenletrendszert:

2. Végezzen "erős" tanulókat.

Oldja meg az egyenletrendszert:

VI. Óra összefoglalója

Kérdések:
Milyen típusú egyenletrendszereket tanultál az órán?
Milyen egyenletrendszer-megoldási módszert alkalmaznak ezek megoldására?

A tanulók által az óra során kapott osztályzatok jelentése.

Bevezetés A projektem problémája, hogy a sikeres vizsgához különféle egyenletrendszerek megoldásának képessége szükséges, és a középiskola során nem jut elég idő a kérdés mélyebb megismerésére. A munka célja: felkészülés a sikeres vizsgaleadásra. A munka feladatai: Bővítse tudását a „szimmetria” fogalmához kapcsolódó matematikai területen. Fejlessze matematikai kultúráját a „szimmetria” fogalmának használatával, amikor szimmetrikusnak nevezett egyenletrendszereket, valamint más matematikai problémákat old meg.

A szimmetria fogalma. Szimmetria - (ógörög συμμετρία), tág értelemben - megváltoztathatatlanság bármilyen átalakítás alatt. Tehát például egy test gömbszimmetriája azt jelenti, hogy a test megjelenése nem változik meg, ha tetszőleges szögben elforgatjuk a térben. A bilaterális szimmetria azt jelenti, hogy a jobb és a bal egyformán néz ki valamely síkhoz képest.

Problémamegoldás szimmetria segítségével. 1. feladat Két ember felváltva tesz le egyforma érméket egy kerek asztalra, és az érmék ne takarják el egymást. Az veszít, aki nem tud mozdulni. Ki nyer, ha helyesen játszanak? (Más szóval, melyik játékosnak van nyerő stratégiája?)

Szimmetrikus rendszerek megoldási módszerei. A szimmetrikus rendszereket a fő szimmetrikus polinomok változóinak változtatásával lehet megoldani. Két ismeretlen x és y egyenlet szimmetrikus rendszerét u = x + y, v = xy helyettesítésével oldjuk meg.

2. példa 3 x 2y - 2xy + 3xy 2 \u003d 78, 2x - 3xy + 2y + 8 \u003d 0 Az alapvető szimmetrikus polinomok felhasználásával a rendszer a következő formában írható fel: 3uv - 2v \u003d 78, 3v \u003d -8. Ha a második egyenletből u = kifejezést adunk, és behelyettesítjük az első egyenletbe, 9v2–28v – 156 = 0 értéket kapunk. Ennek az egyenletnek a gyökei v 1 = 6 és v 2 = - lehetővé teszik, hogy megtaláljuk a megfelelő értékeket u1 = 5, u2= - az u = kifejezésből.

Oldjuk meg most a következő rendszerhalmazt. Oldjuk meg most az x + y = 5, és x + y = - , xy = 6 xy = - rendszerek következő halmazát. x \u003d 5 - y, és y \u003d -x -, xy \u003d 6 xy \u003d -. x \u003d 5 - y, és y \u003d -x -, y (5 - y) \u003d 6 x (-x -) \u003d -. x \u003d 5 - y és y \u003d -x -, y 1 \u003d 3, y 2 \u003d 2 x 1 \u003d, x 2 \u003d - x 1 \u003d 2, x 2 \u0 és 0 1 \u003d, x 2 \u003d - y 1= 3, y 2 =2 y 1 = -, y 2= Válasz: (2; 3), (3; 2), (; -), (- ;).

A szimmetrikus rendszerek megoldásában használt tételek. 1. Tétel (szimmetrikus polinomokon) Két változóban lévő tetszőleges szimmetrikus polinom ábrázolható két alapvető szimmetrikus polinom függvényeként Más szóval, bármely f (x, y) szimmetrikus polinomhoz létezik két változó függvénye φ (u, v) olyan, hogy

2. tétel (szimmetrikus polinomokon) 2. tétel (szimmetrikus polinomokon) Bármelyik szimmetrikus polinom három változóban ábrázolható három alapvető szimmetrikus polinom függvényében: Más szóval, bármely f (x, y) szimmetrikus polinomra van három θ (u, v, w) változó olyan függvénye, hogy

Bonyolultabb szimmetrikus rendszerek - a modult tartalmazó rendszerek: | x – y | + y2 = 3, | x – 1 | + | y-1 | = 2. Tekintsük ezt a rendszert külön x-re< 1 и при х ≥ 1. Если х < 1, то: а) при у < х система принимает вид х – у + у 2 = 3, - х + 1 – у + 1 = 2, или х – у + у 2 = 3, х + у = 0, откуда находим х 1 = 1, у 1 = - 1, х 2 = - 3, у2 = 3. Эти пары чисел не принадлежат к рассматриваемой области;

b) x ≤ y esetén< 1 система принимает вид б) при х ≤ у < 1 система принимает вид - х + у + у 2 = 3, - х + 1 – у + 1 = 2, или - х + у + у 2 = 3, х + у = 0, откуда находим х 1 = 3, у 1 = - 3; х 2 = - 1, у 2 = 1. Эти пары чисел не принадлежат к рассматриваемой области; в) при у ≥ 1 (тогда у >x) a rendszer a következő alakot ölti: - x + y + y 2 \u003d 3, - x + 1 + y - 1 \u003d 2, vagy - x + y + y 2 \u003d 3, x - y \u003d - 2, ahonnan x 1 \u003d - 3, y 1 \u003d - 1, x 2 \u003d - 1, y 2 \u003d 1. A második számpár a vizsgált területhez tartozik, vagyis ez egy megoldás ehhez a rendszerhez.

Ha x ≥ 1, akkor: Ha x ≥ 1, akkor: a) x > y és y< 1 система принимает вид х – у + у 2 = 3, х – 1 – у = 1 = 2, или х – у + у 2= 3, х – у = 2, откуда находим х 1 = 1, у 1 = - 1, х 2 = 4, у 2 = 2. Первая пара чисел принадлежит рассматриваемой области, т. Е. является решением данной системы; б) при х >y és y ≥ 1 a rendszer a következő alakot veszi fel: x - y + y 2 = 3, x - 1 + y - 1 = 2, vagy x - y + y 2 = 3, x + y = 4, amiből x-et kapunk = 1, y = 3. Ez a számpár nem tartozik a vizsgált területhez;

c) x ≤ y (akkor y ≥ 1) esetén a rendszer a c) alakot veszi fel x ≤ y esetén (akkor y ≥ 1), a rendszer - x + y + y 2 = 3, x - 1 + y - 1 = 2, vagy - x + y + y 2 = 3, x + y = 4, ahonnan x 1 = 5 + √8, y 1 = - 1 - √8; x 2 = 5 - √8, y 2 = - 1 + √8. Ezek a számpárok nem tartoznak a vizsgált területhez. Így x 1 \u003d - 1, y 1 \u003d 1; x 2 \u003d 1, y 2 \u003d - 1. Válasz: (- 1; 1); (tizenegy).

Következtetés A matematika fejleszti az emberi gondolkodást, a logikán keresztül tanít különböző megoldásokat találni. Így, miután megtanultam a szimmetrikus rendszerek megoldását, rájöttem, hogy nem csak konkrét példák kiegészítésére, hanem különféle problémák megoldására is használhatók. Úgy gondolom, hogy a projekt nem csak nekem jelenthet hasznot. Aki ezzel a témával is szeretne megismerkedni, annak jó segítője lesz a munkám.

A felhasznált irodalom listája: Bashmakov M.I., "Algebra és az elemzés kezdetei", 2. kiadás, Moszkva, "Prosveshchenie", 1992, 350 oldal. Rudchenko P.A., Yaremchuk F.P., "Algebra és elemi függvények", könyvtár; harmadik, átdolgozott és bővített kiadás; Kijev, Naukova, Dumka, 1987, 648 oldal Sharygin I. F., „Matematika középiskolásoknak”, Moszkva, Drofa kiadó, 1995, 490 oldal Internetes források: http://www.college. en/

A munka felhasználható leckékhez és beszámolókhoz a "Matematika" témában

A kész matematikai prezentációkat vizuális segédeszközként használják, amely lehetővé teszi a tanár vagy a szülő számára, hogy a tankönyvből diák és táblázatok segítségével demonstrálja a tanult témát, példákat mutasson be problémák és egyenletek megoldására, és tesztelje tudását. Az oldal ezen részében rengeteg kész matematika-prezentációt találhat és letölthet 1,2,3,4,5,6 évfolyamos diákoknak, valamint felsőfokú matematikai előadásokat egyetemisták számára.

Tehát megkapjuk az egyenletet Emlékezzünk vissza a polinomok racionális gyökére vonatkozó tételre (2.1.5. pont). Egyenletünk racionális gyökereit a -4 szám osztói között kell keresni. Az összes osztón végignézve meg vagyunk győződve arról, hogy az egyenletnek nincs racionális gyökere. Ez a tétel azonban nem a gyökerek létezésére vonatkozó tétel volt. A megadott tétel csak a következőket mondta ki: ha egy egész együtthatós polinomnak vannak racionális gyökei (de továbbra is fennáll annak a lehetősége, hogy NEM léteznek), akkor ezeknek a gyökeknek valamilyen speciális alakjuk lesz. Azt az esetet, amikor nincsenek racionális gyökerek, ez a tétel nem írja le.

Próbáljuk megkeresni az eredeti rendszer egyenletének gyökereit irracionális számok között. Ehhez azonban némi találékonyságra lesz szükség: a szimmetrikus rendszerek szokásos helyettesítése itt nyilvánvalóan nem működik.

A második egyenletet kockává emelve a következőt kapjuk: így a Vieta-tétel szerint, és a másodfokú egyenlet gyökei így és innen,

Az egyenletrendszerek megoldásának további szakirodalmát tanulmányozva találkoztam egy új típusú rendszerrel - a szimmetrikus rendszerrel. És kitűztem magam elé egy célt:

Foglalja össze a tudományos információkat az "Egyenletrendszerek" témában.

Megérteni és megtanulni, hogyan kell megoldani az új változók bevezetésének módját;

3) Tekintsük a szimmetrikus egyenletrendszerekkel kapcsolatos főbb elméleteket!

4) Tanuljon meg szimmetrikus egyenletrendszereket megoldani.

Egyenletrendszerek megoldásának története.

Az ismeretlenek lineáris egyenletekből való kiküszöbölését régóta alkalmazzák. A 17-18 században. ban ben. a kizárási technikákat Fermat, Newton, Leibniz, Euler, Bezout, Lagrange fejlesztette ki.

A modern jelölésben a két ismeretlennel rendelkező két lineáris egyenlet rendszerének alakja: a1x + b1y = c1, a2x + b2x = c2 x = c1b1 - c2b; y = а1с2 – а2с1 Ennek a rendszernek a megoldásait képletekkel fejezzük ki.

a1b2 – a2b1 a1b2 – a2b1

A 17. században megalkotott koordináta-módszernek köszönhetően. Fermat és Descartes segítségével lehetővé vált az egyenletrendszerek grafikus megoldása.

3-2 évezredben írt óbabiloni szövegekben. e. , sok olyan problémát tartalmaz, amelyeket egyenletrendszerek összeállításával oldanak meg, amelyekben másodfokú egyenleteket is bevezetnek.

1. példa:

Összeadtam a két négyzetem területeit: 25. A második négyzet oldala egyenlő az első oldalával és még 5. A megfelelő egyenletrendszer a megfelelő jelölésben így néz ki: x2 + y2 = 25, y = x = 5

Diophantus, akinek nem volt jelölése sok ismeretlenre, nagyon igyekezett az ismeretlent úgy választani, hogy a rendszer megoldását egyetlen egyenlet megoldására redukálja.

2. példa:

"Keress két természetes számot, tudva, hogy az összegük 20, a négyzetösszege pedig 208."

A feladatot úgy is megoldottuk, hogy összeállítottunk egy egyenletrendszert, x + y = 20, de megoldottuk x2 + y2 = 208

Diophantus, ismeretlennek választva a kívánt számok különbségének felét, azaz.

(x - y) \u003d z, + (x + y) \u003d 10

2z2 + 200 = 208 z = + 2z = -2- nem teljesíti a feladat feltételét, ezért ha z = 2x = 12, és y = 8

Algebrai egyenletrendszer fogalmai.

Sok feladatban szükség lehet több ismeretlen mennyiség megkeresésére, tudva, hogy a segítségükkel képződött más mennyiségek (ismeretlenek függvényei) egyenlők egymással, vagy adott mennyiségekkel. Nézzünk egy egyszerű példát.

Egy 2400 m2 alapterületű téglalap alakú telek 200 m hosszú kerítéssel van bekerítve. keresse meg a szakasz hosszát és szélességét. Valójában ennek a problémának az "algebrai modellje" két egyenletből és egy egyenlőtlenségből álló rendszer.

Az esetleges korlátokat-egyenlőtlenségeket mindig szem előtt kell tartani. Amikor egyenletrendszer-összeállítási feladatokat old meg. De továbbra is az a legfontosabb, hogy magukat az egyenleteket oldjuk meg. Mesélek az alkalmazott módszerekről.

Kezdjük a definíciókkal.

Az egyenletrendszer több (egynél több) egyenletből álló halmaz, amelyeket egy göndör zárójel köt össze.

A göndör zárójel azt jelenti, hogy a rendszer összes egyenletét egyszerre kell végrehajtani, és azt mutatja, hogy meg kell találni egy számpárt (x; y), amely minden egyenletet valódi egyenlőséggé alakít.

A rendszer megoldása egy olyan x és y számpár, amely ebbe a rendszerbe behelyettesítve minden egyenletét valódi numerikus egyenlőséggé alakítja.

Egy egyenletrendszert megoldani azt jelenti, hogy megtaláljuk az összes megoldását, vagy megállapítjuk, hogy nincs ilyen.

Helyettesítő módszer.

A helyettesítési módszer az, hogy az egyik egyenletben az egyik változót egy másikkal fejezzük ki. Az így kapott kifejezést behelyettesítjük egy másik egyenlettel, amely egy változós egyenletté alakul, majd megoldódik. Ennek a változónak a kapott értékeit behelyettesítjük az eredeti rendszer bármely egyenletébe, és megtaláljuk a második változót.

Algoritmus.

1. Fejezd ki y-t x-szel a rendszer egyik egyenletéből.

2. Helyettesítse be a kapott kifejezést y helyett a rendszer egy másik egyenletébe.

3. Oldja meg a kapott egyenletet x-re!

4. Helyettesítsük be egymás után a harmadik lépésben talált egyenlet gyökeit x helyett az első lépésben kapott y-tól x-ig terjedő kifejezésbe.

5) Írja le a választ értékpárok formájában (x; y).

1. számú példa y \u003d x - 1,

Ha behelyettesítjük a második egyenletben y \u003d x - 1, 5x + 2 (x - 1) \u003d 16-ot kapunk, amelyből x \u003d 2. behelyettesítjük a kapott kifejezést az első egyenletbe: y \u003d 2 - 1 \ u003d 1.

Válasz: (2; 1).

2. példa:

8y - x \u003d 4, 1) 2 (8y - 4) - 21y \u003d 2

2x - 21 év \u003d 2 16 év - 8 - 21 év \u003d 2

5 év \u003d 10 x \u003d 8 év - 4, y \u003d -2

2x - 21 év \u003d 2

2) x \u003d 8 * (-2) - 4 x \u003d 8y - 4, x = -20

2 (8 év - 4) - 21 év \u003d 2 x \u003d 8 év - 4, y \u003d -2 x \u003d -20, y \u003d -2

Válasz: (-20; -2).

3. példa: x2 + y +8 = xy, 1) x2 + 2x + 8 = x * 2x y - 2x = 0 x 2 + 2x + 8 = 2x2

X2 + 2x + 8 = 0 x2 + y + 8 = xy, x2 - 2x - 8 = 0 - másodfokú egyenlet y = 2x x1 = -2 x2 = 4 x2 + 2x + 8 = x * 2x 2) y1 = 2 * (-2) y = 2x y1 = -4 y2 = 2 * 4 x1 = -2 y2 = 8 x2 = 4 y = 2x x1 = -2, x2 = 4 y1 = -4, y2 = 8

Ezért (-2; -4); (4; 8) ennek a rendszernek a megoldásai.

Hozzáadás módja.

Az összeadási módszer abból áll, hogy ha egy adott rendszer olyan egyenletekből áll, amelyeket összeadva egy változóval egyenletet alkotnak, akkor ennek az egyenletnek a megoldásával megkapjuk az egyik változó értékét. A második változó értéke megtalálható, mint a helyettesítési módszernél.

Algoritmus rendszerek összeadásos módszerrel történő megoldásához.

1. Egyenlítse ki az egyik ismeretlen együttható moduljait.

2. Összeadva vagy kivonva a kapott egyenleteket, keress egy ismeretlent.

3. A talált értéket behelyettesítve az eredeti rendszer egyik egyenletébe, keresse meg a második ismeretlent.

1. példa. Oldja meg az egyenletrendszert a következő összeadásával: x + y \u003d 20, x - y \u003d 10

Ha kivonjuk a második egyenletet az első egyenletből, azt kapjuk

A második kifejezésből x \u003d 20 - y fejezzük ki

Helyettesítse y \u003d 5 értékét ebben a kifejezésben: x \u003d 20 - 5 x \u003d 15.

Válasz: (15; 5).

2. példa:

A javasolt rendszer egyenleteit ábrázoljuk különbségként, megkapjuk

7y = 21, ahonnan y = 3

Helyettesítsük be ezt az értéket az x = rendszer második egyenletéből kifejezett értékbe, így x = 4-et kapunk.

Válasz: (4; 3).

3. példa:

2x + 11y = 15,

10x - 11y = 9

Ezeket az egyenleteket összeadva a következőt kapjuk:

2x + 10x = 15 + 9

12x \u003d 24 x \u003d 2, ezt az értéket a második egyenletbe behelyettesítve a következőt kapjuk:

10 * 2 - 11y \u003d 9, ahonnan y \u003d 1.

Ennek a rendszernek a megoldása a (2; 1) pár.

Egyenletrendszerek grafikus megoldása.

Algoritmus.

1. Készítsen grafikonokat a rendszer egyes egyenleteiről!

2. A megszerkesztett egyenesek metszéspontjának koordinátáinak megkeresése.

A vonalak kölcsönös elrendezésének esete a síkon.

1. Ha az egyenesek metszik egymást, azaz egy közös pontjuk van, akkor az egyenletrendszernek egy megoldása van.

2. Ha az egyenesek párhuzamosak, azaz nincs közös pontjuk, akkor az egyenletrendszernek nincs megoldása.

3. Ha az egyenesek egybeesnek, azaz sok pontjuk van, akkor az egyenletrendszernek végtelen sok megoldása van.

1. példa:

Oldja meg grafikusan az x - y \u003d -1 egyenletrendszert,

Az y első és második egyenletből fejezzük ki: y \u003d 1 + x, y \u003d 4 - 2x x

Készítsünk grafikonokat a rendszer egyes egyenleteiről:

1) y \u003d 1 + x - a függvény grafikonja egy egyenes x 0 1 (1; 2) y 1 2

2) y \u003d 4 - 2x - a függvény grafikonja egy egyenes x 0 1 y 4 2

Válasz: (1; 2).

2. példa: y x ​​+ 2y = 6,

4y \u003d 8 - 2x x y \u003d, y \u003d y \u003d - a függvény grafikonja egy egyenes x 0 2 y 3 2 y \u003d - a függvény grafikonja egy egyenes x 0 2 y 2 1

Válasz: Nincsenek megoldások.

3. példa: y x ​​- 2y \u003d 2,

3x - 6y \u003d 6 x - 2y \u003d 2, x - 2y \u003d 2 x y \u003d - a függvény grafikonja egy egyenes x 0 2 y -1 0

Válasz: A rendszernek végtelen számú megoldása van.

Új változók bevezetésének módszere.

Az új változók bevezetésének módja az, hogy egy új változót csak egy egyenletbe viszünk be, vagy mindkét egyenlethez egyszerre két új változót, majd az egyenletet vagy egyenleteket az új változókra vonatkozóan megoldjuk, ezután marad egy egyszerűbb rendszer megoldása. egyenletek közül, amelyekből megtaláljuk a kívánt megoldást.

1. példa:

x + y = 5

Jelölje = z, majd =.

Az első egyenlet z + = formájú lesz, ekvivalens a 6z - 13 + 6 = 0-val. A kapott egyenlet megoldása után z = ; z=. Ekkor = vagy =, vagyis az első egyenlet két egyenletre oszlik, ezért két rendszerünk van:

x + y = 5 x + y = 5

Ezen rendszerek megoldásai az adott rendszer megoldásai.

Az első rendszer megoldása a (2; 3) pár, a második pedig a (3; 2) pár.

Ezért a + =, x + y = 5 rendszer megoldásai

A párok (2; 3); (3; 2)

2. példa:

Legyen = X, a = Y.

X \u003d, 5 * - 2Y \u003d 1

5X - 2Y \u003d 1 2,5 (8 - 3Y) - 2Y \u003d 1

20 - 7,5 U - 2U \u003d 1

X \u003d, -9,5Y \u003d -19

5 * - 2Y = 1 Y = 2

Csináljunk cserét.

2 x = 1, y = 0,5

Válasz: (1; 0,5).

Szimmetrikus egyenletrendszerek.

Az n ismeretlent tartalmazó rendszert szimmetrikusnak nevezzük, ha nem változik az ismeretlenek átrendezésekor.

Két ismeretlen x és y egyenlet szimmetrikus rendszerét u = x + y, v = xy helyettesítésével oldjuk meg. Megjegyzendő, hogy a szimmetrikus rendszerekben előforduló kifejezéseket u-val és v-vel fejezzük ki. Adjunk néhány olyan példát, amelyek kétségtelenül érdekesek sok szimmetrikus rendszer megoldásához: x2 + y2 = (x + y)2 - 2xy = u2 - 2v, x3 + y3 = (x + y)(x2 - xy + y2) = u ( u2 - 2v - v) = u3 - 3uv, x4 + y4 = (x2 + y2)2 - 2x2y2 = (u2 - 2v)2 - 2v2 = u4 - 4u2v + 2v2, x2 + xy + y2 = u2 - 2v + v = u2 - v stb.

Az x y, z ismeretlenek három egyenletének szimmetrikus rendszerét x + y + z = u, xy + yz + xz = w helyettesítésével oldjuk meg. Ha u, v, w található, akkor egy t2 – ut2 + vt – w = 0 köbegyenlet keletkezik, melynek t1, t2, t3 gyökei különböző permutációkban az eredeti rendszer megoldásai. Az ilyen rendszerekben a leggyakoribb kifejezéseket u, v, w a következőképpen fejezzük ki: x2 + y2 + z2 = u2 - 2v x3 + y3 + z3 = u3 - 3uv + 3w

1. példa: x2 + xy + y2 = 13, x + y = 4

Legyen x + y = u, xy = v.

u2 – v = 13, u = 4

16 - v = 13, u = 4 v = 3, u = 4

Csináljunk cserét.

Válasz: (1; 3); (3; 1).

2. példa: x3 + y3 = 28, x + y = 4

Legyen x + y = u, xy = v.

u3 – 3uv = 28, u = 4

64 - 12 v = 28, u = 4

12v = -36 u = 4 v = 3, u = 4

Csináljunk cserét.

x + y = 4, xy = 3 x = 4 - y xy = 3 x = 4 - y,

(4 – y) y = 3 x = 4 – y, y1 = 3; y2 = 1 x1 = 1, x2 = 3, y1 = 3, y2 = 1

Válasz: (1; 3); (3; 1).

3. példa: x + y + xy = 7, x2 + y2 + xy = 13

Legyen x = y = u, xy = v.

u + v = 7, u2 - v = 13 u2 - v = 13 u2 - 7 + u =13 u2 + u = 20 v = 7 - u, u (u + 1) =20 u2 - v =13 u = 4 v = 7 – u, u = 4 v = 3, u = 4

Csináljunk cserét.

x + y = 4, xy = 3 x = 4 - y xy = 3 x = 4 - y,

(4 – y) y = 3 x = 4 – y, y1 = 3; y2 = 1 x1 = 1, x2 = 3, y1 = 3, y2 = 1

Válasz: (1; 3); (3; 1).

4. példa: x + y = 5, x3 + y3 = 65

Legyen x + y = u, xy = v.

u = 5, u3 - 3uv = 65 u3 - 3uv = 65 125 - 15v = 65

15v = -60 u = 5, v = 4 v = 4

Csináljunk cserét.

x + y = 5, xy = 4 x = 5 - y, xy = 4 x = 5 - y, y (5 - y) = 4 x = 5 - y y1 = 1, y2 = 4 x1 = 4, x2 = 1, y1 = 1, y2 = 4

Válasz: (4; 1); (tizennégy).

5. példa: x2 + xy + y2 = 49, x + y + xy = 23

Változtassuk meg az ismeretleneket, a rendszer u2 + v = 49, u + v = 23 alakot ölt.

Ezeket az egyenleteket összeadva azt kapjuk, hogy u2 + u - 72 = 0 gyökök u1 = 8, u2 = -9. Ennek megfelelően v1 = 15, v2 = 32. Marad az x + y = 8, x + y = -9, xy = 15 xy = 32 rendszerek halmazának megoldása.

Az x + y = 8 rendszernek vannak megoldásai: x1 = 3, y1 = 5; x2=5, y2=3.

Az x + y = -9 rendszernek nincsenek valós megoldásai.

Válasz: (3; 5), (5; 3).

6. számú példa. Oldja meg az egyenletrendszert!

2x2 - 3xy + 2y2 = 16, x + xy + y + 3 = 0

Az u = y + x és v = xy alapszimmetrikus polinomok felhasználásával a következő egyenletrendszert kapjuk

2u2 - 7v = 16, u + v = -3

A rendszer második egyenletéből a v = -3 – u kifejezést behelyettesítve az első egyenletbe, a következő 2u2 + 7u + 5 = 0 egyenletet kapjuk, melynek gyöke u1 = -1 és u2 = -2,5; és ennek megfelelően a v1 = -2 és v2 = -0,5 értékeket v = -3 - u-ból kapjuk.

Most már meg kell oldani a következő rendszerkészletet x + y \u003d -1 és x + y \u003d -2,5, xy \u003d -2 xy \u003d -0,5

Ennek a rendszerhalmaznak, tehát az eredeti rendszernek (ekvivalenciájuk miatt) megoldásai a következők: (1; -2), (-2; 1), (;).

7. példa:

3x2y - 2xy + 3x2 \u003d 78,

2x - 3xy + 2y + 8 = 0

Az alapvető szimmetrikus polinomok felhasználásával a rendszer a következő formában írható fel

3uv - 2v = 78,

Ha a második egyenletből u = kifejezést adunk és behelyettesítjük az első egyenletbe, 9v2 – 28v – 156 = 0 eredményt kapunk. Ennek az egyenletnek a gyökei v1 = 6 és v2 = - lehetővé teszik, hogy megtaláljuk a megfelelő u1 = 5 értékeket, u2 = - az u = kifejezésből.

Most megoldjuk a következő rendszerkészletet x + y \u003d 5 és x + y \u003d - , xy \u003d 6 xy \u003d -.

x \u003d 5 - y, és y \u003d -x -, xy \u003d 6 xy \u003d -.

x \u003d 5 - y, és y \u003d -x -, y (5 - y) \u003d 6 x (-x -) \u003d -.

x = 5 – y és y = -x - , y1 = 3, y2 =2 x1 = , x2 = - x1 = 2, x2 = 3 és x1 = , x2 = - y1 = 3, y2 =2 y1 = -, y2 =

Válasz: (2; 3), (3; 2), (; -), (-;).

Következtetés.

A cikk írása során különböző típusú algebrai egyenletrendszerekkel ismerkedtem meg. Összefoglaló tudományos információk az "Egyenletrendszerek" témában.

Megértette és megtanulta a megoldást új változók bevezetésével;

Áttekintette a szimmetrikus egyenletrendszerekkel kapcsolatos főbb elméleteket

Megtanulta szimmetrikus egyenletrendszerek megoldását.

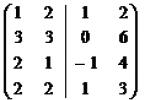
− 4 1 + 4

−6

27 ≡ 0,

−4 x + 4 év + 27

+(y +6 )

x = 1, x

(x − 1 )

= −6.

y = −6

Vegyük észre, hogy a második egyenlet megoldása még nem a rendszer megoldása. A kapott számokat be kell cserélni a rendszer fennmaradó első egyenletébe. Ebben az esetben a helyettesítés után azonosságot kapunk.

Válasz: (1, - 6).♦

§öt. Homogén egyenletek és rendszerek
f(x, y) függvény	hívott	homogén		k ha
f (tx, ty ) = tk f (x, y ) .	Például az f (x, y) = 4x 3 y − 5xy 3 + x 2 y 2 függvény
fokú homogén, hiszen		f(tx,ty) = 4	(tx )3 (ty )− 5 (tx )(ty )3 +
+ (tx ) 2 (ty) 2 = t 4 (4x 3 y − 5xy 3 + x 2 y 2 ). Az f (x, y) egyenlet = 0, ahol				f (x, y) -

a homogén függvényt homogénnek nevezzük. Az egyenletre redukálódik

egy ismeretlennel, ha bevezetünk egy új t = x y változót.

f (x, y) = a,

Két változós rendszer g (x, y) = b, ahol f (x, y) , g (x, y) -

Az azonos fokú homogén függvényeket homogénnek nevezzük. Ha ab ≠ 0, szorozzuk meg az első egyenletet b-vel, a másodikat a-val, és

összehasonlítjuk egyiket a másikkal - egyenértékű rendszert kapunk

bf (x, y) − ag(x, y) = 0, g(x, y) = b.

Az első egyenlet a t = változók változásával

(vagy t =

) értékre csökkenti

egyenlet egy ismeretlennel.

Ha a = 0

(b = 0) , akkor az f (x, y) egyenlet = 0 (g (x, y) = 0)

változók t =

(vagy t =

) egy egyenletté redukál egy ismeretlent

− xy + y

21 ,

20. példa (Moszkvai Állami Egyetem, 2001, kémia tanszék) Oldja meg a rendszert

− 2xy + 15 = 0.

2012-2013 tanév évf., 1. szám, 11 cella. Matematika. Algebrai egyenletek, egyenlőtlenségek, rendszerek

− xy + y 2 = 21,

− xy + y 2

y2 − 2xy

-2xy = -15

2xy = -15

x ≠ 0, y ≠ 0;

19 ± 11

5x2 - 19xy + 12y2 = 0 5

− 19

12 = 0

-2xy = -15

x = 3 év,

y = ±5.

3 ) ,

(− 3 3; −

3 ) , (4; 5) ,

(− 4; − 5) . ♦

6. §. Szimmetrikus rendszerek

f(x, y)

hívott

szimmetrikus,

f(x, y) = f(y, x) .

f (x, y) = a

Forma egyenletrendszere

ahol f (x , y ), g (x , y ) szimmet-

g (x, y) = b,

ric, szimmetrikus rendszernek nevezzük. Ilyen rendszerek

gyakrabban	csak újak bevezetésével	változók
x + y = u, xy

x 3 + x 3 y 3 + y 3 = 17,

21. példa. Egyenletrendszer megoldása

x + xy + y = 5 .

♦ Ez egy algebrai (szimmetrikus) rendszer, amelyet általában x + y = u , xy = v változtatásával oldanak meg. Ezt észrevéve

x 3 + x 3 y 3 + y 3 = (x + y ) (x 2 − xy + y 2 ) + x 3 y 3 =

= (x + y ) ((x + y) 2 - 3 xy) + x3 y3 = u (u2 - 3 v) + v3,

írja át a rendszert a formába

© 2012, ZFTSH MIPT. Kolesnikova Sofia Ilyinichna

2012-2013 tanév évf., 1. szám, 11 cella. Matematika. Algebrai egyenletek, egyenlőtlenségek, rendszerek

− 3uv + v

u = 5 − v,

6 = 0

V=5

−5V

v = 3, u = 2

(régi változókban)

x + y = 2,

x = 2 − y ,

xy = 3,

y 2 − 2 y + 3 = 0

x + y = 3,

x = 3 − y,

x=2, y=1,

y −3 y + 2 = 0

x=1, y=2.

xy = 2,

Válasz: (2;1),

(1; 2) . ♦

Irodalom

1. S. I. Kolesnikova "Intenzív felkészítés az egységes államvizsgára." Moszkva, Iris - sajtó;

2. "Az egységes államvizsga összetett problémáinak megoldása" Moszkva, Iris - Press vagy "Wako", 2011;

3. „Potenciális” magazin №№1-2 2005-re - S. I. Kolesnikova cikkei „Irracionális egyenletek” és „Irracionális egyenlőtlenségek”;

4. S. I. Kolesnikov "Irracionális egyenletek", Moszkva, 2010,

OOO "Azbuka";

5. S. I. Kolesnikova „Irracionális egyenlőtlenségek”, Moszkva, 2010, Azbuka LLC;

6. S. I. Kolesnikova „Modulokat tartalmazó egyenletek és egyenlőtlenségek”, Moszkva, 2010, Azbuka LLC.

tesztkérdések

1. (2) bekezdése alapján. Határozzuk meg az 5x + 1 ≥ 2(x − 1) egyenlőtlenség összes megoldását tartalmazó intervallum legkisebb hosszát.

2. (2) bekezdése alapján. Oldja meg az x 3 + 8x 2 − 20x ≤ 2x − 4 egyenlőtlenséget (nem kell megoldani a köbegyenletet, mivel jobb és bal oldalon x − 2 tényező van).

3. (2) bekezdése alapján. Oldja meg a 2 − x ≥ x − 3 egyenlőtlenséget.

4. (2) bekezdése alapján. Keresse meg a rés legkisebb hosszát, amelyhez tartozik

betakarítsák az egyenlőtlenség összes megoldását	x2 + 5 x – 84	≤ 0 .
	(x + 13 ) (x + 14 )

5. (3) bekezdése alapján. Határozzuk meg az egyenlőtlenség egész megoldásainak négyzetösszegét!

© 2012, ZFTSH MIPT. Kolesnikova Sofia Ilyinichna

2012-2013 tanév évf., 1. szám, 11 cella. Matematika. Algebrai egyenletek, egyenlőtlenségek, rendszerek

4 − x − 8 + x ≤ x +6 .

6. (3) bekezdése alapján. Oldja meg az 5 + x − 8 − x ≤ 3 − x egyenlőtlenséget.

7. (3) bekezdése alapján. Oldja meg az egyenlőtlenséget		− x 3 − x −1			≤x.
						9 − 4x − (x + 3) )
8. (3) bekezdése alapján. Oldja meg az egyenlőtlenséget		4 − x −(x + 2 ) )(					≤ 0.
			(x + 1 ) (x - 2 ) (x - 3 )

9. (4) bekezdése alapján. Keresse meg a rés legkisebb hosszát, amelyhez tartozik

betakarítsák az egyenlőtlenség összes megoldását
			x+5				x+2				144-x< 0.
			X-2				4 x -5		6x-6

10. (2) bekezdése alapján. Határozzuk meg a 8 x − 8 ≤ 32 + 4x − x 2 egyenlőtlenség összes megoldását tartalmazó intervallum legkisebb hosszát!

11. (4) bekezdése alapján. Határozzuk meg az összes egész megoldás négyzetösszegét

2. (2) bekezdése alapján. Keresse meg a legrövidebb intervallumot, amely tartalmazza
			(x − 1 )3 (x + 3 )
az egyenlőtlenség összes megoldása										≤ 0 .
			2x-1				x − 2		) (x − 1 )

3. (2) bekezdése alapján. Oldja meg az egyenlőtlenséget

4 (x − 3 ) 4 ≥ 4 (x − 7 .5 ) 4 .

4. (4) bekezdése alapján. Oldja meg az egyenlőtlenséget

x2 + 3 x - 4

x2-16

2x 2 + 3x - 20

5. (3) bekezdése alapján. Oldja meg az egyenlőtlenséget (x 2	X +1 ) 2 -2 x 3 + x 2 + x -3 x 2		≥ 0 .
4 − 2x − 1 ≤ 3.	Feladatok
	- 5x + 6 + 9 - 2x - 5	≤ 0 .
1. (3) bekezdése. Oldja meg az egyenlőtlenséget
19x 2 - 4x 3 - 4x + 19

10x2-17x-6

6. (4) bekezdése alapján. Keresse meg mindazt, amelyre az egyenlet

4 x -

f (x) \u003d x 2 + 4x + függvény

x 2 -

x − 1

− a csak elfogadja

nem negatív

szilárd értékek.

8. (4) bekezdése alapján. Oldja meg a 4 x − 3 egyenletet!

x − 1

5x + 14 - 3

5x + 14 - 1

9. (4) bekezdése alapján. Oldja meg az egyenletet

x 2 − 5 +

x 2 −3 = x +1 +

x + 3.

24-x2

9 2 x

10. (3) bekezdése alapján. Oldja meg az egyenlőtlenséget

≥ 0 .

x2 - 4 7 x - 10

11. (3) bekezdése alapján. Három versenyző indul egy időben a pálya azonos pontjáról, és állandó sebességgel hajt ugyanabba az irányba. Az első versenyző először utolérte a másodikat, megtéve ötödik körét, a rajttal homlokegyenest ellenkező ponton, majd fél órával ezután másodszor is utolérte a harmadikat, a rajt pillanatát nem számítva. . A második versenyző 3 órával a rajt után utolérte először a harmadikat. Hány kört tesz meg óránként az első versenyző, ha a második legalább húsz perc alatt teljesíti a kört?

© 2012, ZFTSH MIPT. Kolesnikova Sofia Ilyinichna