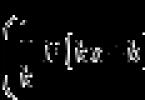ვიდეო გაკვეთილი „ფუნქციების პერიოდულობა y = sin x, y = cos x“ ავლენს ფუნქციის პერიოდულობის ცნებას, განიხილავს ამოცანების ამოხსნის მაგალითების აღწერას, რომლებშიც გამოყენებულია ფუნქციის პერიოდულობის ცნება. ეს ვიდეო გაკვეთილი არის ვიზუალური დამხმარე საშუალება მოსწავლეებისთვის თემის ახსნისთვის. ასევე, ეს სახელმძღვანელო შეიძლება გახდეს გაკვეთილის დამოუკიდებელი ნაწილი, ათავისუფლებს მასწავლებელს მოსწავლეებთან ინდივიდუალური მუშაობის ჩასატარებლად.

ამ თემის წარმოდგენის ხილვადობა ძალიან მნიშვნელოვანია. ფუნქციის ქცევის წარმოსადგენად, მისი შედგენისას, უნდა იყოს ვიზუალიზაცია. ყოველთვის არ არის შესაძლებელი დაფისა და ცარცის გამოყენებით კონსტრუქციების გაკეთება ისე, რომ ყველა მოსწავლისთვის გასაგები იყოს. ვიდეო ტუტორიალში შესაძლებელია აგებისას ნახატის ნაწილების ფერით გამოყოფა და ანიმაციის გამოყენებით ტრანსფორმაციების გაკეთება. ამრიგად, კონსტრუქციები უფრო გასაგები ხდება სტუდენტების უმეტესობისთვის. ასევე, ვიდეოგაკვეთილის მახასიათებლები ხელს უწყობს მასალის უკეთ დამახსოვრებას.

დემონსტრაცია იწყება გაკვეთილის თემის გაცნობით, ასევე წინა გაკვეთილებზე ნასწავლი მასალის შეხსენებით. კერძოდ, შეჯამებულია იმ თვისებების ჩამონათვალი, რომლებიც იდენტიფიცირებული იყო y = sin x ფუნქციებში, ასევე y = cos x. განსახილველი ფუნქციების თვისებებს შორის აღინიშნება განმარტების დომენი, მნიშვნელობების დიაპაზონი, პარიტეტი (უცნაობა), სხვა ნიშნები - შეზღუდულობა, ერთფეროვნება, უწყვეტობა, უმცირესი (უმეტესის) მნიშვნელობის წერტილები. მოსწავლეებს ეცნობებათ, რომ ამ გაკვეთილზე შეისწავლება ფუნქციის კიდევ ერთი თვისება - პერიოდულობა.

პერიოდული ფუნქციის განმარტება y=f(x), სადაც xϵX, რომელშიც წარმოდგენილია პირობა f(x-Т)= f(x)= f(x+Т) ზოგიერთი Т≠0-ისთვის. წინააღმდეგ შემთხვევაში, რიცხვს T ეწოდება ფუნქციის პერიოდი.

განსახილველი სინუსური და კოსინუსური ფუნქციებისთვის პირობის შესრულება მოწმდება შემცირების ფორმულების გამოყენებით. აშკარაა, რომ იდენტობის ფორმა sin(x-2π)=sinx=sin(x+2π) შეესაბამება ფუნქციის პერიოდულობის პირობის განმსაზღვრელ გამოთქმის ფორმას. იგივე თანასწორობა შეიძლება აღინიშნოს კოსინუსისთვის cos (x-2π)= cos x= cos (x+2π). ეს ნიშნავს, რომ ეს ტრიგონომეტრიული ფუნქციები პერიოდულია.

შემდგომში აღნიშნულია, თუ როგორ ეხმარება პერიოდულობის თვისება პერიოდული ფუნქციების გრაფიკების აგებას. განიხილება ფუნქცია y = sin x. ეკრანზე აგებულია კოორდინატთა სიბრტყე, რომელზედაც აბსციები -6π-დან 8π-მდე აღინიშნება π საფეხურით. სიბრტყეზე გამოსახულია სინუს გრაფიკის ნაწილი, რომელიც წარმოდგენილია სეგმენტზე ერთი ტალღით. ფიგურა გვიჩვენებს, თუ როგორ ყალიბდება ფუნქციის გრაფიკი განსაზღვრების მთელ დომენზე, აგებული ფრაგმენტის გადაადგილებით, რაც იწვევს გრძელ სინუსოიდს.

y = cos x ფუნქციის გრაფიკი აგებულია მისი პერიოდულობის თვისების გამოყენებით. ამისათვის ფიგურაში აგებულია კოორდინატთა სიბრტყე, რომელზეც გამოსახულია გრაფიკის ფრაგმენტი. აღნიშნულია, რომ ასეთი ფრაგმენტი, როგორც წესი, აგებულია სეგმენტზე [-π/2;3π/2]. სინუსური ფუნქციის გრაფიკის მსგავსად, კოსინუს გრაფის აგება ხორციელდება ფრაგმენტის გადაადგილებით. კონსტრუქციის შედეგად წარმოიქმნება გრძელი სინუსოიდი.

პერიოდული ფუნქციის გრაფიკას აქვს ფუნქციები, რომელთა გამოყენებაც შესაძლებელია. ამიტომ ისინი მოცემულია განზოგადებული ფორმით. აღნიშნულია, რომ ასეთი ფუნქციის გრაფიკის ასაგებად ჯერ აშენდება გრაფიკის განშტოება T სიგრძის გარკვეულ ინტერვალზე. შემდეგ საჭიროა აგებული ტოტის გადატანა მარჯვნივ და მარცხნივ T, 2T, 3T, და ა.შ. ამავე დროს, აღინიშნება პერიოდის კიდევ ერთი თვისება - ნებისმიერი მთელი რიცხვისთვის k≠0 რიცხვი kT ასევე არის ფუნქციის პერიოდი. ამასთან, T-ს უწოდებენ მთავარ პერიოდს, რადგან ის ყველაზე პატარაა. ტრიგონომეტრიული ფუნქციების სინუსისა და კოსინუსის ძირითადი პერიოდია 2π. თუმცა პერიოდებიც არის 4π, 6π და ა.შ.

შემდეგი, შემოთავაზებულია განიხილოს y = cos 5x ფუნქციის ძირითადი პერიოდის პოვნა. ამოხსნა იწყება იმ ვარაუდით, რომ T არის ფუნქციის პერიოდი. ეს ნიშნავს, რომ პირობა f(x-T)= f(x)= f(x+T) უნდა დაკმაყოფილდეს. ამ იდენტობაში f(x)= cos 5x და f(x+T)=cos 5(x+T)= cos (5x+5T). ამ შემთხვევაში cos (5x+5T)= cos 5x, შესაბამისად 5T=2πn. ახლა შეგიძლიათ იპოვოთ T=2π/5. პრობლემა მოგვარებულია.

მეორე ამოცანაში თქვენ უნდა იპოვოთ y=sin(2x/7) ფუნქციის ძირითადი პერიოდი. ვარაუდობენ, რომ T ფუნქციის ძირითადი პერიოდი მოცემული ფუნქციისთვის არის f(x)= sin(2x/7), ხოლო პერიოდის შემდეგ f(x+T)=sin(2x/7)(x+T) = sin(2x/7 +(2/7)T). შემცირების შემდეგ ვიღებთ (2/7)Т=2πn. თუმცა, ჩვენ უნდა ვიპოვოთ ძირითადი პერიოდი, ამიტომ ვიღებთ უმცირეს მნიშვნელობას (2/7)T=2π, საიდანაც ვპოულობთ T=7π. პრობლემა მოგვარებულია.

დემონსტრაციის დასასრულს მაგალითების შედეგები შეჯამებულია ფუნქციის ძირითადი პერიოდის განსაზღვრის წესის შესაქმნელად. აღნიშნულია, რომ y=sinkx და y=coskx ფუნქციებისთვის ძირითადი პერიოდებია 2π/k.

ვიდეოგაკვეთილი „ფუნქციების პერიოდულობა y = sin x, y = cos x“ შეიძლება გამოყენებულ იქნას მათემატიკის ტრადიციულ გაკვეთილზე გაკვეთილის ეფექტურობის გაზრდის მიზნით. ასევე რეკომენდირებულია, რომ ეს მასალა გამოიყენოს მასწავლებელმა, რომელიც უზრუნველყოფს დისტანციურ სწავლებას, რათა გაიზარდოს განმარტების სიცხადე. ვიდეო შეიძლება რეკომენდაცია გაუწიოს მებრძოლ სტუდენტს თემის გაგების გასაღრმავებლად.

ტექსტის გაშიფვრა:

"ფუნქციების პერიოდულობა y = cos x, y = sin x."

y = sin x და y = cos x ფუნქციების გრაფიკების ასაგებად, გამოყენებული იქნა ფუნქციების თვისებები:

1 განმარტების არე,

2 ღირებულების ფართობი,

3 ლუწი ან კენტი,

4 ერთფეროვნება,

5 შეზღუდვა,

6 უწყვეტობა,

7 უმაღლესი და ყველაზე დაბალი ღირებულება.

დღეს ჩვენ შევისწავლით კიდევ ერთ თვისებას: ფუნქციის პერიოდულობას.

განმარტება. ფუნქციას y = f (x), სადაც x ϵ X (ბერძნული უდრის x-ის ef-ს, სადაც x ეკუთვნის x სიმრავლეს), ეწოდება პერიოდული, თუ არის არა ნულოვანი რიცხვი T ისეთი, რომ ნებისმიერი x-ისთვის სიმრავლე X მოქმედებს ორმაგი თანასწორობა: f (x - T)= f (x) = f (x + T) (eff x-დან მინუს te უდრის ef x-დან და უდრის ef x-დან პლუს te). T რიცხვს, რომელიც აკმაყოფილებს ამ ორმაგ ტოლობას, ეწოდება ფუნქციის პერიოდი

და რადგან სინუსი და კოსინუსი განსაზღვრულია მთელ რიცხვთა წრფეზე და ნებისმიერი x-სთვის ტოლობები sin(x - 2π)= sin x= sin(x+ 2π) დაკმაყოფილებულია (სინუსი x-ს გამოკლებული ორი pi უდრის x-ის სინუსს და ტოლია x-ის სინუსს პლუს ორი პი ) და

cos (x- 2π)= cos x = cos (x+ 2π) (x-ს გამოკლებული ორი pi უდრის x-ის კოსინუსს და ტოლია x-ის კოსინუსს პლუს ორი pi), მაშინ სინუსი და კოსინუსი პერიოდული ფუნქციებია პერიოდი 2π.

პერიოდულობა საშუალებას გაძლევთ სწრაფად შექმნათ ფუნქციის გრაფიკი. მართლაც, y = sin x ფუნქციის გრაფიკის ასაგებად საკმარისია ერთი ტალღის გამოსახვა (ყველაზე ხშირად სეგმენტზე (ნულიდან ორ პი-მდე), შემდეგ კი გრაფიკის აგებული ნაწილის x-ის გასწვრივ გადატანა. -ღერძი მარჯვნივ და მარცხნივ 2π-ით, შემდეგ 4π-ით და ასე შემდეგ, რათა მიიღოთ სინუსური ტალღა.

(მარჯვნივ და მარცხნივ გადანაცვლების ჩვენება 2π, 4π)

ანალოგიურად ფუნქციის გრაფიკისთვის

y = cos x, მაგრამ ჩვენ ვაშენებთ ერთ ტალღას ყველაზე ხშირად სეგმენტზე [; ] (მინუს პი-დან ორიდან სამ პი-მდე ორზე).

მოდით შევაჯამოთ ზემოაღნიშნული და გამოვიტანოთ დასკვნა: პერიოდული ფუნქციის გრაფიკის ასაგებად T პერიოდით, ჯერ უნდა ააგოთ გრაფიკის განშტოება (ან ტალღა, ან ნაწილი) T სიგრძის ნებისმიერ ინტერვალზე (ყველაზე ხშირად ეს არის შუალედი ბოლოებით 0 და T წერტილებში ან - და (მინუს te ორი და te ორი), შემდეგ გადაიტანეთ ეს ტოტი x(x) ღერძის გასწვრივ მარჯვნივ და მარცხნივ T, 2T, 3T და ა.შ.

ცხადია, თუ ფუნქცია პერიოდულია T პერიოდით, მაშინ ნებისმიერი მთელი რიცხვისთვის k0 (ka არ არის ნულის ტოლი) kT ფორმის რიცხვი (ka te) ასევე არის ამ ფუნქციის პერიოდი. როგორც წესი, ისინი ცდილობენ გამოყოს ყველაზე პატარა პოზიტიური პერიოდი, რომელსაც მთავარ პერიოდს უწოდებენ.

როგორც y = cos x, y = sin x ფუნქციების პერიოდი, შეიძლება ავიღოთ - 4π, 4π, - 6π, 6π და ა.შ. (მინუს ოთხი pi, ოთხი pi, მინუს ექვსი pi, ექვსი pi და ა.შ.) . მაგრამ რიცხვი 2π არის ორივე ფუნქციის მთავარი პერიოდი.

მოდით შევხედოთ მაგალითებს.

მაგალითი 1. იპოვეთ y = cos5x ფუნქციის ძირითადი პერიოდი (y უდრის ხუთ x-ის კოსინუსს).

გამოსავალი. ვთქვათ T იყოს y = cos5x ფუნქციის ძირითადი პერიოდი. დავაყენოთ

f (x) = cos5x, შემდეგ f (x + T) = cos5(x + T) = cos (5x + 5T) (eff x-ს პლუს te უდრის კოსინუსს ხუთის გამრავლებული x-ის ჯამზე და te არის ხუთი x და ხუთი ტე-ის ჯამის კოსინუსის ტოლია).

cos (5x + 5T) = cos5x. აქედან გამომდინარე, 5T = 2πn (ხუთი ტე უდრის ორ პი ენს), მაგრამ პირობის მიხედვით თქვენ უნდა იპოვოთ ძირითადი პერიოდი, რაც ნიშნავს 5T = 2π. ვიღებთ T=

(ამ ფუნქციის პერიოდი არის ორი პი გაყოფილი ხუთზე).

პასუხი: T=.

მაგალითი 2. იპოვეთ y = sin ფუნქციის ძირითადი პერიოდი (y უდრის ორი x-ის შვიდის კოეფიციენტის სინუსს).

გამოსავალი. ვთქვათ T იყოს y = sin ფუნქციის ძირითადი პერიოდი. დავაყენოთ

f (x) = sin, შემდეგ f (x + T) = sin (x + T) = sin (x + T) (ef x-ს პლუს te უდრის ორი მეშვიდედის ნამრავლის სინუსს და x-ის ჯამს. და ტე უდრის ორი მეშვიდე x და ორი მეშვიდე ტეს ჯამის სინუსს.

იმისათვის, რომ რიცხვი T იყოს ფუნქციის პერიოდი, უნდა დაკმაყოფილდეს იდენტურობა

sin (x + T) = ცოდვა. აქედან გამომდინარე T= 2πn (ორი მეშვიდე te უდრის ორ პი ენს), მაგრამ პირობის მიხედვით უნდა იპოვოთ ძირითადი პერიოდი, რაც ნიშნავს T= 2π. ვიღებთ T=7

(ამ ფუნქციის პერიოდი არის შვიდი პი).

პასუხი: T=7.

მაგალითებში მიღებული შედეგების შეჯამებით შეგვიძლია დავასკვნათ: y = sin kx ან y = cos kx ფუნქციების ძირითადი პერიოდი (y უდრის sine ka x ან y უდრის კოსინუს ka x) ტოლია (ორი pi. გაყოფილი კა).

>> ფუნქციების პერიოდულობა y = sin x, y = cos x

§ 11. ფუნქციების პერიოდულობა y = sin x, y = cos x

წინა აბზაცებში გამოვიყენეთ ფუნქციების შვიდი თვისება: განსაზღვრის დომენი, ლუწი ან კენტი, ერთფეროვნება, შეზღუდულობა, უდიდესი და უმცირესი მნიშვნელობები, უწყვეტობა, ფუნქციის მნიშვნელობების დიაპაზონი. ჩვენ გამოვიყენეთ ეს თვისებები ან ფუნქციის გრაფიკის ასაგებად (ეს მოხდა, მაგალითად, § 9-ში), ან აგებული გრაფიკის წასაკითხად (ეს მოხდა, მაგალითად, § 10-ში). ახლა დადგა ხელსაყრელი მომენტი, რომ შემოვიტანოთ ფუნქციების კიდევ ერთი (მერვე) თვისება, რომელიც ნათლად ჩანს ზემოთ აგებულ y = sin x (იხ. სურ. 37), y = cos x (იხ. სურ. 41) ფუნქციების გრაფიკებზე.

განმარტება. ფუნქციას პერიოდული ეწოდება, თუ არსებობს არა ნულოვანი რიცხვი T ისეთი, რომ სიმრავლეებში ნებისმიერი x-ისთვის მოქმედებს ორმაგი თანასწორობა:

T რიცხვს, რომელიც აკმაყოფილებს მითითებულ პირობას, ეწოდება y = f(x) ფუნქციის პერიოდი.
აქედან გამომდინარეობს, რომ ნებისმიერი x-ისთვის ტოლობები მოქმედებს:

მაშინ y = sin x, y = cos x ფუნქციები პერიოდულია და რიცხვი არის 2 პემსახურება როგორც პერიოდს ორივე ფუნქციისთვის.
ფუნქციის პერიოდულობა არის ფუნქციების დაპირებული მერვე თვისება.

ახლა შეხედეთ y = sin x ფუნქციის გრაფიკს (სურ. 37). სინუსუსური ტალღის ასაგებად საკმარისია მისი ერთ-ერთი ტალღის გამოსახვა (სეგმენტზე და შემდეგ გადაიტანოს ეს ტალღა x ღერძის გასწვრივ. შედეგად, ერთი ტალღის გამოყენებით ავაშენებთ მთელ გრაფიკს.

იმავე კუთხით შევხედოთ y = cos x ფუნქციის გრაფიკს (სურ. 41). ჩვენ ვხედავთ, რომ აქ, გრაფიკის გამოსაყენებლად, საკმარისია ჯერ ერთი ტალღის დახატვა (მაგალითად, სეგმენტზე

შემდეგ გადაიტანეთ იგი x ღერძის გასწვრივ
შეჯამებით, ჩვენ ვაკეთებთ შემდეგ დასკვნას.

თუ ფუნქციას y = f(x) აქვს T წერტილი, მაშინ ფუნქციის გრაფიკის ასაგებად ჯერ უნდა ააშენოთ გრაფიკის ტოტი (ტალღა, ნაწილი) T სიგრძის ნებისმიერ ინტერვალზე (ყველაზე ხშირად აიღეთ ინტერვალი ბოლოებთან. წერტილებში და შემდეგ გადაიტანეთ ეს ტოტი x ღერძის გასწვრივ მარჯვნივ და მარცხნივ T, 2T, ZT და ა.შ.
პერიოდულ ფუნქციას აქვს უსასრულოდ ბევრი პერიოდი: თუ T არის პერიოდი, მაშინ 2T არის პერიოდი, ხოლო ZT არის პერიოდი და -T არის პერიოდი; ზოგადად, წერტილი არის KT ფორმის ნებისმიერი რიცხვი, სადაც k = ±1, ±2, ± 3... როგორც წესი, ისინი ცდილობენ, თუ ეს შესაძლებელია, გამოყოს უმცირესი დადებითი პერიოდი; მას უწოდებენ მთავარ პერიოდს.
ასე რომ, 2pk ფორმის ნებისმიერი რიცხვი, სადაც k = ±1, ± 2, ± 3, არის y = sinn x, y = cos x ფუნქციების პერიოდი; 2n არის ორივე ფუნქციის ძირითადი პერიოდი.

მაგალითი. იპოვნეთ ფუნქციის ძირითადი პერიოდი:

ა) ვთქვათ T იყოს y = sin x ფუნქციის ძირითადი პერიოდი. დავაყენოთ

იმისთვის, რომ რიცხვი T იყოს ფუნქციის პერიოდი, იდენტურობა, მაგრამ, რადგან ჩვენ ვსაუბრობთ ძირითადი პერიოდის პოვნაზე, მივიღებთ
ბ) ვთქვათ T იყოს y = cos 0,5x ფუნქციის ძირითადი პერიოდი. დავდოთ f(x)=cos 0.5x. შემდეგ f(x + T)=cos 0.5(x + T)=cos (0.5x + 0.5T).

იმისათვის, რომ რიცხვი T იყოს ფუნქციის პერიოდი, უნდა შეიცავდეს იდენტობის cos (0.5x + 0.5T) = cos 0.5x.

ეს ნიშნავს 0,5 ტ = 2 pp. მაგრამ, რადგან ჩვენ ვსაუბრობთ ძირითადი პერიოდის პოვნაზე, ვიღებთ 0,5T = 2 ლ, T = 4 ლ.

მაგალითში მიღებული შედეგების განზოგადება შემდეგი დებულებაა: ფუნქციის ძირითადი პერიოდი

ა.გ. მორდკოვიჩის ალგებრა მე-10 კლასი

გაკვეთილის შინაარსიგაკვეთილის ჩანაწერები მხარდამჭერი ჩარჩო გაკვეთილის პრეზენტაციის დაჩქარების მეთოდები ინტერაქტიული ტექნოლოგიები ივარჯიშეამოცანები და სავარჯიშოები თვითშემოწმების სემინარები, ტრენინგები, შემთხვევები, კვესტები საშინაო დავალების განხილვის კითხვები რიტორიკული კითხვები სტუდენტებისგან ილუსტრაციებიაუდიო, ვიდეო კლიპები და მულტიმედიური ფოტომასალა, სურათები, გრაფიკები, ცხრილები, დიაგრამები, იუმორი, ანეკდოტები, ხუმრობები, კომიქსები, იგავი, გამონათქვამები, კროსვორდები, ციტატები დანამატებიაბსტრაქტები სტატიები რჩევები კურიოზული საწოლის ფურცლებისთვის სახელმძღვანელოების ძირითადი და ტერმინების დამატებითი ლექსიკონი სხვა სახელმძღვანელოების და გაკვეთილების გაუმჯობესებასახელმძღვანელოში შეცდომების გამოსწორება, სახელმძღვანელოში ფრაგმენტის განახლება გაკვეთილზე ინოვაციის ელემენტები, მოძველებული ცოდნის შეცვლა ახლით მხოლოდ მასწავლებლებისთვისიდეალური გაკვეთილების კალენდარული გეგმა წლის მეთოდოლოგიური რეკომენდაციების განხილვის პროგრამები ინტეგრირებული გაკვეთილები

2020 წლის ივლისში NASA იწყებს ექსპედიციას მარსზე. კოსმოსური ხომალდი მარსს მიაწვდის ელექტრონულ საშუალებას ექსპედიციის ყველა რეგისტრირებული მონაწილის სახელებით.

მონაწილეთა რეგისტრაცია ღიაა. მიიღეთ ბილეთი მარსზე ამ ბმულით.

თუ ამ პოსტმა გადაჭრა თქვენი პრობლემა ან უბრალოდ მოგეწონათ, გაუზიარეთ ბმული თქვენს მეგობრებს სოციალურ ქსელებში.

კოდის ერთ-ერთი ვარიანტი უნდა იყოს კოპირებული და ჩასმული თქვენი ვებ გვერდის კოდში, სასურველია ტეგებს შორის და ან ტეგის შემდეგ დაუყოვნებლივ. პირველი ვარიანტის მიხედვით MathJax უფრო სწრაფად იტვირთება და ნაკლებად ანელებს გვერდს. მაგრამ მეორე ვარიანტი ავტომატურად აკონტროლებს და ატვირთავს MathJax-ის უახლეს ვერსიებს. თუ პირველ კოდს ჩასვამთ, ის პერიოდულად უნდა განახლდეს. თუ მეორე კოდს ჩასვამთ, გვერდები უფრო ნელა იტვირთება, მაგრამ არ დაგჭირდებათ MathJax-ის განახლებების მუდმივი მონიტორინგი.

MathJax-ის დასაკავშირებლად უმარტივესი გზაა Blogger-ში ან WordPress-ში: საიტის მართვის პანელში დაამატეთ ვიჯეტი, რომელიც შექმნილია მესამე მხარის JavaScript კოდის ჩასართავად, დააკოპირეთ მასში ზემოთ წარმოდგენილი ჩამოტვირთვის კოდის პირველი ან მეორე ვერსია და მოათავსეთ ვიჯეტი უფრო ახლოს. შაბლონის დასაწყისამდე (სხვათა შორის, ეს საერთოდ არ არის საჭირო, რადგან MathJax სკრიპტი ასინქრონულად იტვირთება). Სულ ეს არის. ახლა ისწავლეთ MathML, LaTeX და ASCIIMathML მარკირების სინტაქსი და მზად ხართ ჩასვათ მათემატიკური ფორმულები თქვენი საიტის ვებ გვერდებში.

კიდევ ერთი ახალი წლის ღამე... ყინვაგამძლე ამინდი და ფიფქები ფანჯრის მინაზე... ამ ყველაფერმა მიბიძგა კიდევ ერთხელ დავწერო... ფრაქტალებზე და რა იცის ამის შესახებ ვოლფრამ ალფამ. ამ თემაზე არის საინტერესო სტატია, რომელიც შეიცავს ორგანზომილებიანი ფრაქტალური სტრუქტურების მაგალითებს. აქ ჩვენ განვიხილავთ სამგანზომილებიანი ფრაქტალების უფრო რთულ მაგალითებს.

ფრაქტალი შეიძლება ვიზუალურად იყოს წარმოდგენილი (აღწერილი) როგორც გეომეტრიული ფიგურა ან სხეული (რაც ნიშნავს, რომ ორივე არის ერთობლიობა, ამ შემთხვევაში, წერტილების ერთობლიობა), რომლის დეტალებსაც იგივე ფორმა აქვს, რაც თავად თავდაპირველ ფიგურას. ანუ, ეს არის საკუთარი თავის მსგავსი სტრუქტურა, რომლის დეტალების შესწავლისას გადიდებისას დავინახავთ იგივე ფორმას, რაც გადიდების გარეშე. მაშინ როცა ჩვეულებრივი გეომეტრიული ფიგურის შემთხვევაში (არა ფრაქტალი), გადიდებისას დავინახავთ დეტალებს, რომლებსაც უფრო მარტივი ფორმა აქვთ, ვიდრე თავად თავდაპირველი ფიგურა. მაგალითად, საკმარისად მაღალი გადიდებისას, ელიფსის ნაწილი სწორი ხაზის სეგმენტს ჰგავს. ეს არ ხდება ფრაქტალებთან: მათი ნებისმიერი გაზრდისას ჩვენ კვლავ დავინახავთ იმავე კომპლექსურ ფორმას, რომელიც კვლავ და ისევ მეორდება ყოველი გაზრდისას.

ბენუა მანდელბროტი, ფრაქტალების მეცნიერების ფუძემდებელი, თავის სტატიაში ფრაქტალები და ხელოვნება მეცნიერების სახელით წერდა: „ფრაქტალები არის გეომეტრიული ფორმები, რომლებიც ისეთივე რთულია მათი დეტალებით, როგორც მთლიანი ფორმით. ანუ, თუ ფრაქტალის ნაწილია. გადიდდება მთლიანის ზომამდე, გამოჩნდება მთლიანობაში, ან ზუსტად, ან შესაძლოა მცირე დეფორმაციით“.

ტრიგონომეტრიული ფუნქციები პერიოდულია, ანუ მეორდება გარკვეული პერიოდის შემდეგ. შედეგად, საკმარისია ამ ინტერვალზე ფუნქციის შესწავლა და აღმოჩენილი თვისებების გაფართოება ყველა სხვა პერიოდზე.

ინსტრუქციები

1. თუ მოგეცემათ პრიმიტიული გამოხატულება, რომელშიც არის მხოლოდ ერთი ტრიგონომეტრიული ფუნქცია (sin, cos, tg, ctg, sec, cosec), ხოლო ფუნქციის შიგნით კუთხე არ მრავლდება არცერთ რიცხვზე და ის თავად არ არის ამაღლებული. ნებისმიერი ხარისხით - გამოიყენეთ განმარტება. sin, cos, sec, cosec შემცველი გამონათქვამებისთვის თამამად დააყენეთ პერიოდი 2P-ზე, ხოლო თუ განტოლება შეიცავს tg, ctg, მაშინ P. ვთქვათ, y=2 sinx+5 ფუნქციისთვის წერტილი იქნება 2P-ის ტოლი. .

2. თუ კუთხე x ტრიგონომეტრიული ფუნქციის ნიშნის ქვეშ გამრავლებულია რომელიმე რიცხვზე, მაშინ ამ ფუნქციის პერიოდის საპოვნელად გაყავით ტიპიური პერიოდი ამ რიცხვზე. ვთქვათ, თქვენ გეძლევათ ფუნქცია y = sin 5x. სინუსისთვის ტიპიური პერიოდია 2P; მისი გაყოფით 5-ზე მიიღებთ 2P/5 - ეს არის ამ გამოხატვის სასურველი პერიოდი.

3. ხარისხამდე ამაღლებული ტრიგონომეტრიული ფუნქციის პერიოდის საპოვნელად შეაფასეთ სიმძლავრის პარიტეტი. თანაბარი ხარისხისთვის, შეამცირეთ ტიპიური პერიოდი ნახევარით. ვთქვათ, თუ მოგეცემათ ფუნქცია y = 3 cos^2x, მაშინ ტიპიური პერიოდი 2P შემცირდება 2-ჯერ, ასე რომ პერიოდი იქნება P-ის ტოლი. გთხოვთ გაითვალისწინოთ, რომ tg, ctg ფუნქციები პერიოდულია P-ზე ყველასთვის. ხარისხი.

4. თუ მოგეცემათ განტოლება, რომელიც შეიცავს ორი ტრიგონომეტრიული ფუნქციის ნამრავლს ან კოეფიციენტს, ჯერ იპოვეთ ყველა მათგანის წერტილი ცალ-ცალკე. ამის შემდეგ იპოვეთ მინიმალური რიცხვი, რომელიც შეიცავდა ორივე პერიოდის მთელ რიცხვს. ვთქვათ, მოცემულია ფუნქცია y=tgx*cos5x. ტანგენტისთვის პერიოდი არის P, კოსინუსისთვის 5x პერიოდი არის 2P/5. მინიმალური რაოდენობა, რომელშიც ორივე პერიოდი შეიძლება განთავსდეს, არის 2P, შესაბამისად სასურველი პერიოდია 2P.

5. თუ გიჭირთ შემოთავაზებულის გაკეთება ან შედეგში ეჭვი გეპარებათ, შეეცადეთ გააკეთოთ ის, როგორც განსაზღვრულია. აიღეთ T, როგორც ფუნქციის პერიოდი; ის აღემატება ნულს. ჩაანაცვლეთ გამონათქვამი (x + T) x-ის ნაცვლად განტოლებაში და ამოხსენით მიღებული ტოლობა თითქოს T იყოს პარამეტრი ან რიცხვი. შედეგად, თქვენ აღმოაჩენთ ტრიგონომეტრიული ფუნქციის მნიშვნელობას და შეძლებთ იპოვოთ უმცირესი პერიოდი. ვთქვათ, რელიეფის შედეგად მიიღებთ პირადობის ცოდვას (T/2) = 0. T-ის მინიმალური მნიშვნელობა, რომელზეც ის შესრულებულია, არის 2P, ეს იქნება დავალების შედეგი.

პერიოდული ფუნქცია არის ფუნქცია, რომელიც იმეორებს მის მნიშვნელობებს გარკვეული არანულოვანი პერიოდის შემდეგ. ფუნქციის პერიოდი არის რიცხვი, რომელიც ფუნქციის არგუმენტს რომ ემატება, არ ცვლის ფუნქციის მნიშვნელობას.

დაგჭირდებათ

• დაწყებითი მათემატიკის ცოდნა და საბაზისო მიმოხილვა.

ინსტრუქციები

1. f(x) ფუნქციის პერიოდი ავღნიშნოთ K რიცხვით. ჩვენი ამოცანაა აღმოვაჩინოთ K-ის ეს მნიშვნელობა. ამისათვის წარმოიდგინეთ, რომ ფუნქცია f(x), პერიოდული ფუნქციის განსაზღვრის გამოყენებით, ვატოლებთ f(x+K)=f(x).

2. მიღებულ განტოლებას ვხსნით უცნობი K-ის მიმართ, თითქოს x იყოს მუდმივი. K-ის მნიშვნელობიდან გამომდინარე, რამდენიმე ვარიანტი იქნება.

3. თუ K>0 – მაშინ ეს არის თქვენი ფუნქციის პერიოდი, თუ K=0 – ფუნქცია f(x) არ არის პერიოდული, თუ f(x+K)=f(x) განტოლების ამონახსნი აქვს. არ არსებობს ნებისმიერი K-ისთვის, რომელიც არ არის ნულის ტოლი, მაშინ ასეთ ფუნქციას ეწოდება აპერიოდული და მას ასევე არ აქვს წერტილი.

ვიდეო თემაზე

Შენიშვნა!
ყველა ტრიგონომეტრიული ფუნქცია პერიოდულია და ყველა მრავალწევრი ფუნქცია 2-ზე მეტი ხარისხის არის აპერიოდული.

სასარგებლო რჩევა
2 პერიოდული ფუნქციისგან შემდგარი ფუნქციის პერიოდი არის ამ ფუნქციების პერიოდების უმცირესი უნივერსალური ჯერადი.

ტრიგონომეტრიული განტოლებები არის განტოლებები, რომლებიც შეიცავს უცნობი არგუმენტის ტრიგონომეტრიულ ფუნქციებს (მაგალითად: 5sinx-3cosx =7). იმისათვის, რომ ისწავლოთ მათი გადაჭრა, თქვენ უნდა იცოდეთ ამის გაკეთების რამდენიმე გზა.

ინსტრუქციები

1. ასეთი განტოლებების ამოხსნა შედგება 2 ეტაპისგან, პირველი არის განტოლების რეფორმირება მისი უმარტივესი ფორმის მისაღებად. უმარტივესი ტრიგონომეტრიული განტოლებებია: Sinx=a; Cosx=a და ა.შ.

2. მეორე არის მიღებული უმარტივესი ტრიგონომეტრიული განტოლების ამოხსნა. არსებობს ამ ტიპის განტოლებების ამოხსნის ძირითადი გზები: ამოხსნა ალგებრულად. ეს მეთოდი ცნობილია სკოლიდან, ალგებრის კურსიდან. სხვაგვარად უწოდებენ ცვლადის ჩანაცვლებისა და ჩანაცვლების მეთოდს. შემცირების ფორმულების გამოყენებით, ჩვენ გარდაქმნით, ვაკეთებთ ჩანაცვლებას და შემდეგ ვიპოვით ფესვებს.

3. განტოლების ფაქტორინგი. პირველ რიგში, ყველა ტერმინს გადავიტანთ მარცხნივ და ვაფასებთ მათ.

4. განტოლების დაყვანა ერთგვაროვანზე. განტოლებებს უწოდებენ ერთგვაროვან განტოლებებს, თუ ყველა წევრი ერთნაირი ხარისხისაა, ხოლო სინუსი და კოსინუსი ერთი და იგივე კუთხით. გადაიტანეთ ყველა უნივერსალური ფაქტორი ფრჩხილებიდან; ფაქტორებისა და ფრჩხილების გათანაბრება ნულთან; გათანაბრებული ფრჩხილები იძლევა ქვედა ხარისხის ერთგვაროვან განტოლებას, რომელიც უნდა გაიყოს cos-ზე (ან sin) უმაღლეს ხარისხზე; ამოხსენით მიღებული ალგებრული განტოლება ტანთან დაკავშირებით.

5. შემდეგი მეთოდი ნახევარ კუთხეზე გადატანაა. თქვით, ამოხსენით განტოლება: 3 sin x – 5 cos x = 7. გადავიდეთ ნახევარ კუთხეზე: 6 sin (x / 2) · cos (x / 2) – 5 cos? (x / 2) + 5 ცოდვა ? (x / 2) = 7 ცოდვა? (x / 2) + 7 cos ? (x/ 2) , რის შემდეგაც ვამცირებთ ყველა წევრს ერთ ნაწილად (სასურველია მარჯვენა მხარეს) და ვხსნით განტოლებას.

6. დამხმარე კუთხის შეყვანა. როდესაც ჩვენ შევცვლით cos(a) ან sin(a) მთელ რიცხვს. ნიშანი "ა" არის დამხმარე კუთხე.

7. პროდუქტის ჯამად რეფორმირების მეთოდი. აქ თქვენ უნდა გამოიყენოთ შესაბამისი ფორმულები. ვთქვათ მოცემული: 2 sin x · sin 3x = cos 4x ამოხსენით მარცხენა მხარის ჯამად გარდაქმნით, ანუ: cos 4x – cos 8x = cos 4x ,cos 8x = 0 ,8x = p / 2 + pk , x = p / 16 + pk / 8.

8. საბოლოო მეთოდს მრავალფუნქციური ჩანაცვლება ეწოდება. გამოვხატავთ გამონათქვამს და ვაკეთებთ ცვლილებას, ვთქვათ Cos(x/2)=u და შემდეგ ვხსნით განტოლებას u პარამეტრით. ტოტალის შეძენისას მნიშვნელობას საპირისპიროდ ვაქცევთ.

ვიდეო თემაზე

თუ განვიხილავთ წერტილებს წრეზე, მაშინ წერტილები x, x + 2π, x + 4π და ა.შ. ემთხვევა ერთმანეთს. ამრიგად, სწორი ხაზის ტრიგონომეტრიული ფუნქციები პერიოდულად იმეორებს მათ მნიშვნელობას. თუ ფუნქციის პერიოდი ცნობილია, შესაძლებელია ამ პერიოდზე ფუნქციის აგება და სხვებზე გამეორება.

ინსტრუქციები

1. პერიოდი არის რიცხვი T ისეთი, რომ f(x) = f(x+T). პერიოდის საპოვნელად ამოხსენით შესაბამისი განტოლება, არგუმენტის სახით ჩაანაცვლეთ x და x+T. ამ შემთხვევაში ფუნქციებისთვის უკვე კარგად ცნობილ პერიოდებს იყენებენ. სინუსის და კოსინუსური ფუნქციებისთვის პერიოდი არის 2π, ხოლო ტანგენსისა და კოტანგენსისთვის - π.

2. მოცემულია ფუნქცია f(x) = sin^2(10x). განვიხილოთ გამოთქმა sin^2(10x) = sin^2(10(x+T)). გამოიყენეთ ფორმულა ხარისხის შესამცირებლად: sin^2(x) = (1 – cos 2x)/2. შემდეგ მიიღებთ 1 – cos 20x = 1 – cos 20(x+T) ან cos 20x = cos (20x+20T). იმის ცოდნა, რომ კოსინუსის პერიოდი არის 2π, 20T = 2π. ეს ნიშნავს T = π/10. T არის მინიმალური სწორი პერიოდი და ფუნქცია განმეორდება 2T და 3T შემდეგ და სხვა მიმართულებით ღერძის გასწვრივ: -T, -2T და ა.შ.

სასარგებლო რჩევა
გამოიყენეთ ფორმულები ფუნქციის ხარისხის შესამცირებლად. თუ უკვე იცით ზოგიერთი ფუნქციის პერიოდები, შეეცადეთ შეამციროთ არსებული ფუნქცია ცნობილამდე.

ფუნქციის ტოლობისა და უცნაურობის შესწავლა ხელს უწყობს ფუნქციის გრაფიკის აგებას და მისი ქცევის ბუნების გაგებას. ამ კვლევისთვის, თქვენ უნდა შეადაროთ ეს ფუნქცია დაწერილი არგუმენტისთვის "x" და არგუმენტისთვის "-x".

ინსტრუქციები

1. ჩაწერეთ ფუნქცია, რომლის შესწავლაც გსურთ y=y(x) სახით.

2. შეცვალეთ ფუნქციის არგუმენტი „-x“-ით. ჩაანაცვლეთ ეს არგუმენტი ფუნქციურ გამოსახულებაში.

3. გამოთქმის გამარტივება.

4. ამრიგად, თქვენ გაქვთ იგივე ფუნქცია დაწერილი არგუმენტებისთვის "x" და "-x". შეხედეთ ამ ორ ჩანაწერს: თუ y(-x)=y(x), მაშინ ეს არის ლუწი ფუნქცია, თუ y(-x)=-y(x), მაშინ ეს არის კენტი ფუნქცია. თუ შეუძლებელია ფუნქციის შესახებ ვთქვათ, რომ y (-x)=y(x) ან y(-x)=-y(x), მაშინ პარიტეტის თვისებით ეს არის უნივერსალური ფორმის ფუნქცია. ანუ არც ლუწია და არც კენტი.

5. ჩაწერეთ თქვენი დასკვნები. ახლა თქვენ შეგიძლიათ გამოიყენოთ ისინი ფუნქციის გრაფიკის ასაგებად ან ფუნქციის თვისებების მომავალ ანალიტიკურ კვლევაში.

6. ასევე შესაძლებელია ფუნქციის თანაბარობაზე და უცნაურობაზე საუბარი იმ შემთხვევაშიც, როცა უკვე მოცემულია ფუნქციის გრაფიკი. ვთქვათ, გრაფიკი მსახურობდა ფიზიკური ექსპერიმენტის შედეგად, თუ ფუნქციის გრაფიკი სიმეტრიულია ორდინატთა ღერძის მიმართ, მაშინ y(x) არის ლუწი ფუნქცია. თუ ფუნქციის გრაფიკი სიმეტრიულია აბსცისის ღერძის მიმართ, მაშინ x(y) არის ლუწი ფუნქცია. x(y) არის y(x) ფუნქციის შებრუნებული ფუნქცია. თუ ფუნქციის გრაფიკი სიმეტრიულია საწყისის მიმართ (0,0), მაშინ y(x) არის კენტი ფუნქცია. შებრუნებული ფუნქცია x(y) ასევე კენტი იქნება.

7. მნიშვნელოვანია გვახსოვდეს, რომ ფუნქციის უთანასწორობისა და უცნაურობის იდეა პირდაპირ კავშირშია ფუნქციის განსაზღვრის სფეროსთან. თუ, ვთქვათ, ლუწი ან კენტი ფუნქცია არ არსებობს x=5-ზე, მაშინ ის არ არსებობს x=-5-ზე, რაც არ შეიძლება ითქვას უნივერსალური ფორმის ფუნქციაზე. ლუწი და კენტი პარიტეტის დადგენისას ყურადღება მიაქციეთ ფუნქციის დომენს.

8. თანაბარობისა და უცნაურობის ფუნქციის პოვნა დაკავშირებულია ფუნქციის მნიშვნელობების სიმრავლის პოვნასთან. ლუწი ფუნქციის მნიშვნელობების სიმრავლის საპოვნელად საკმარისია ფუნქციის ნახევარს შევხედოთ ნულის მარჯვნივ ან მარცხნივ. თუ x>0-ზე ლუწი ფუნქცია y(x) იღებს მნიშვნელობებს A-დან B-მდე, მაშინ მიიღებს იგივე მნიშვნელობებს და x0-ზე კენტი ფუნქცია y(x) იღებს მნიშვნელობების დიაპაზონს A-დან. B-მდე, შემდეგ x sin^2-ზე? + cos^2 ? = 1. მესამე და მეოთხე იდენტობები მიიღება, შესაბამისად, b^2 და a^2-ზე გაყოფით: a^2/b^2 + 1 = c^2/b^2 => tg^2 ? + 1 = 1/cos^2 ?;1 + b^2/a^2 = c^2/a^2 => 1 + 1/tg^2 ? = 1/ცოდვა ^ ? ან 1 + ctg^2? = 1/sin^2 ?. მეხუთე და მეექვსე ძირითადი იდენტობები დასტურდება მართკუთხა სამკუთხედის მახვილი კუთხეების ჯამის განსაზღვრით, რომელიც უდრის 90° ან?/2. უფრო რთული ტრიგონომეტრიული იდენტობები: არგუმენტების დამატების ფორმულები, ორმაგი და სამმაგი კუთხეები, ხარისხის შემცირება, ფუნქციების ჯამის ან ნამრავლების რეფორმირება, აგრეთვე ტრიგონომეტრიული ჩანაცვლების ფორმულები, კერძოდ ძირითადი ტრიგონომეტრიული ფუნქციების გამოსახულებები რუჯის ნახევარი კუთხით: sin ?= (2*tg ?/2)/ (1 + tan^2 ?/2);cos ? = (1 – tg^2 ?/2)/(1 = tg^2 ?/2);tg ? = (2*tg ?/2)/(1 – tg^2 ?/2).

მათემატიკური ფუნქციის მინიმალური მნიშვნელობის პოვნის აუცილებლობა ფაქტობრივად საინტერესოა გამოყენებითი ამოცანების გადასაჭრელად, ვთქვათ, ეკონომიკაში. ზარალის მინიმიზაციას დიდი მნიშვნელობა აქვს ბიზნეს საქმიანობისთვის.

ინსტრუქციები

1. ფუნქციის მინიმალური მნიშვნელობის საპოვნელად საჭიროა განვსაზღვროთ x0 არგუმენტის რა სიდიდეზე დაკმაყოფილდება y(x0) უტოლობა? y(x), სად x? x0. ჩვეულებისამებრ, ეს პრობლემა მოგვარებულია გარკვეულ ინტერვალზე ან ფუნქციის მნიშვნელობების თითოეულ დიაპაზონში, თუ არ არის მითითებული. გადაწყვეტის ერთ-ერთი ასპექტი არის ფიქსირებული წერტილების პოვნა.

2. სტაციონარული წერტილი არის არგუმენტის მნიშვნელობა, რომლის დროსაც ფუნქციის წარმოებული ხდება ნული. ფერმას თეორემის მიხედვით, თუ დიფერენცირებადი ფუნქცია რაღაც მომენტში იღებს უკიდურეს მნიშვნელობას (ამ შემთხვევაში, ლოკალურ მინიმუმს), მაშინ ეს წერტილი სტაციონარულია.

3. ფუნქცია ხშირად იღებს თავის მინიმალურ მნიშვნელობას ზუსტად ამ ეტაპზე, მაგრამ მისი უცვლელად განსაზღვრა შეუძლებელია. უფრო მეტიც, ყოველთვის არ არის შესაძლებელი ზუსტად იმის თქმა, თუ რის ტოლია ფუნქციის მინიმუმი ან იღებს თუ არა მას უსასრულოდ მცირე მნიშვნელობა. შემდეგ, ჩვეულებისამებრ, ისინი პოულობენ იმ ზღვარს, რომლისკენაც იგი მიდრეკილია კლებისას.

4. ფუნქციის მინიმალური მნიშვნელობის დასადგენად აუცილებელია ოთხი ეტაპისგან შემდგარი მოქმედებების თანმიმდევრობის შესრულება: ფუნქციის განსაზღვრის დომენის პოვნა, ფიქსირებული წერტილების მოპოვება, ამ ფუნქციის მნიშვნელობების გადახედვა. ქულები და ინტერვალის ბოლოებში მინიმალურის პოვნა.

5. გამოდის, რომ რომელიმე ფუნქცია y(x) იყოს მოცემული A და B წერტილების საზღვრების მქონე ინტერვალზე. იპოვეთ მისი განმარტების დომენი და გაარკვიეთ არის თუ არა ინტერვალი მისი ქვესიმრავლე.

6. გამოთვალეთ ფუნქციის წარმოებული. მიღებულ გამოსახულებას გაუტოლეთ ნულს და იპოვეთ განტოლების ფესვები. შეამოწმეთ არის თუ არა ეს სტაციონარული წერტილები უფსკრულის ფარგლებში. თუ არა, მაშინ ისინი არ განიხილება შემდგომ ეტაპზე.

7. შეისწავლეთ უფსკრული საზღვრების ტიპზე: ღია, დახურული, რთული ან განუზომელი. ეს განსაზღვრავს, თუ როგორ ეძებთ მინიმალურ მნიშვნელობას. ვთქვათ, სეგმენტი [A, B] არის დახურული ინტერვალი. შეაერთეთ ისინი ფუნქციაში და გამოთვალეთ მნიშვნელობები. იგივე გააკეთე სტაციონარული წერტილით. აირჩიეთ ყველაზე დაბალი ჯამი.

8. ღია და განუზომელი ინტერვალებით სიტუაცია გარკვეულწილად რთულია. აქ მოგიწევთ მოძებნოთ ცალმხრივი საზღვრები, რომლებიც უცვლელად არ იძლევა ცალსახა შედეგს. ვთქვათ, ერთი დახურული და ერთი პუნქცია საზღვრის მქონე ინტერვალისთვის [A, B), უნდა ვიპოვოთ ფუნქცია x = A-ზე და ცალმხრივი ლიმიტი lim y x-ზე? B-0.