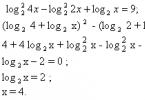Үндсэн ойлголтууд
Тодорхойлолтуудаас эхэлье тэгш, сондгой, үечилсэн функцууд.
Тодорхойлолт 2
Бие даасан хувьсагчийн тэмдэг өөрчлөгдөхөд утга нь өөрчлөгддөггүй функцийг тэгш функц гэнэ.
Тодорхойлолт 3
Тодорхой хугацааны интервалаар утгуудаа давтдаг функц:
T нь функцийн үе юм.
Тэгш ба сондгой тригонометрийн функцууд
Дараах зургийг авч үзье (Зураг 1).
Зураг 1.
Энд $\overrightarrow(OA_1)=(x_1,y_1)$ ба $\overrightarrow(OA_2)=(x_2,y_2)$ нь $Ox$ тэнхлэгтэй харьцуулахад нэгж урттай тэгш хэмтэй векторууд юм.
Мэдээжийн хэрэг, эдгээр векторуудын координатууд нь дараах харилцаатай холбоотой байдаг.
Синус ба косинусын тригонометрийн функцийг нэгж тригонометрийн тойрог ашиглан тодорхойлж болох тул синус функц нь сондгой, косинусын функц нь тэгш функц байх болно, өөрөөр хэлбэл:
Тригонометрийн функцүүдийн үечлэл
Дараах зургийг авч үзье (Зураг 2).

Зураг 2.
Энд $\overrightarrow(OA)=(x,y)$ нь нэгж урттай вектор байна.
$\overrightarrow(OA)$ вектороор бүтэн эргэлт хийцгээе. Өөрөөр хэлбэл, өгөгдсөн векторыг $2\pi $ радианаар эргүүлье. Үүний дараа вектор анхны байрлалдаа бүрэн буцаж ирнэ.
Синус ба косинусын тригонометрийн функцийг нэгж тригонометрийн тойрог ашиглан тодорхойлж болох тул бид үүнийг олж авна.
Өөрөөр хэлбэл, синус болон косинусын функцууд нь $T=2\pi $ хамгийн бага үетэй үечилсэн функцууд юм.
Одоо тангенс ба котангенсийн функцуудыг авч үзье. $tgx=\frac(sinx)(cosx)$ тул
$сtgx=\frac(cosx)(sinx)$ тул
Тригонометрийн функцүүдийн тэгш, сондгой, үечилсэн байдлыг ашиглах асуудлын жишээ
Жишээ 1
Дараах мэдэгдлийг нотлох:
a) $tg(385)^0=тг(25)^0$
в) $sin((-721)^0)=-sin1^0$
a) $tg(385)^0=тг(25)^0$
Шүргэгч нь $(360)^0$ хамгийн бага хугацаатай үечилсэн функц тул бид олж авна
б) $(cos \left(-13\pi \right)\ )=-1$
Косинус нь хамгийн бага хугацаа $2\pi $ байх тэгш ба үечилсэн функц тул бид олж авна
\[(cos \left(-13\pi \баруун)\ )=(cos 13\pi \ )=(cos \left(\pi +6\cdot 2\pi \баруун)=cos\pi \ )=- нэг\]
в) $sin((-721)^0)=-sin1^0$
Синус нь хамгийн бага хугацаа $(360)^0$ байх сондгой, үечилсэн функц тул бид олж авна.
Хэрэв бид эх цэг дээр төвлөрсөн нэгж тойрог байгуулж, аргументийн дурын утгыг тогтоовол x0мөн тэнхлэгээс тоол Үхэрбулан x 0, тэгвэл нэгж тойрог дээрх энэ өнцөг ямар нэг цэгтэй тохирч байна А(Зураг 1) ба түүний тэнхлэг дээрх проекц Өөцэг байх болно М. Урт тайрах ОМцэгийн абсциссийн үнэмлэхүй утгатай тэнцүү А. өгөгдсөн аргументийн утга x0зурагласан функцийн утга y= cos x 0 цэгийн абсцисса хэлбэрээр ГЭХДЭЭ. Үүний дагуу цэг AT(x 0 ;цагт 0) функцийн графикт хамаарна цагт= cos X(Зураг 2). Хэрэв цэг ГЭХДЭЭтэнхлэгийн баруун талд байрладаг OU, Токосин эерэг, зүүн талд байвал сөрөг байх болно. Гэхдээ ямар ч тохиолдолд гол зүйл ГЭХДЭЭтойргоос гарч чадахгүй. Тиймээс косинус нь -1-ээс 1 хооронд хэлбэлздэг:
-1 = cos x = 1.

Дурын өнцөгт нэмэлт эргэлт, 2-ын үржвэр х, цэгийг буцаана Аижил газар. Тиймээс функц у= cos xх:
учир нь ( x+ 2х) = cos x.
Хэрэв бид үнэмлэхүй утгаараа тэнцүү боловч тэмдгээр эсрэг тэсрэг аргументийн хоёр утгыг авбал, xба - x, тойрог дээрх харгалзах цэгүүдийг ол А хболон А-х. Зурагт үзүүлсэн шиг. 3 Тэдний тэнхлэг дээрх проекц Өөижил цэг юм М. Тийм ч учраас
учир нь(- x) = cos( x),

тэдгээр. косинус бол тэгш функц, е(–x) = е(x).
Тиймээс бид функцийн шинж чанарыг судалж болно y= cos Xсегмент дээр , дараа нь түүний паритет, үе үеийг харгалзан үзнэ.
At X= 0 оноо ГЭХДЭЭтэнхлэг дээр байрладаг Өө, түүний абсцисса нь 1, тиймээс cos 0 = 1. Өсөлттэй Xцэг ГЭХДЭЭтойргийн эргэн тойронд дээш, зүүн тийш хөдөлдөг, түүний проекц нь мэдээжийн хэрэг зөвхөн зүүн тийш, х = хувьд х/2 косинус 0 болно. Цэг Аэнэ мөчид энэ нь хамгийн дээд өндөрт хүрч, дараа нь зүүн тийшээ хөдөлж байгаа боловч аль хэдийн доошилж байна. Түүний абсцисса нь -1-тэй тэнцүү хамгийн бага утгад хүрэх хүртэл буурсаар байна X= х. Тиймээс сегмент дээр функц цагт= cos X 1-ээс –1 хүртэл монотон буурдаг (Зураг 4, 5).

Косинусын паритетаас үзэхэд [– интервал дээр байна. х, 0] үед функц нь -1-ээс 1 хүртэл нэг хэвийн өсөж, тэг утгыг авна. x =–х/2. Хэрэв та хэд хэдэн сарын тэмдэг авбал долгион муруй болно (Зураг 6).
Тиймээс функц y= cos xцэгүүдэд тэг утгыг авдаг X= х/2 + кп, хаана к-дурын бүхэл тоо. Цэг дээр 1-тэй тэнцүү дээд цэгт хүрнэ X= 2кп, өөрөөр хэлбэл 2-р алхамтай х, мөн цэгүүдийн минимум нь –1-тэй тэнцүү байна X= х + 2кп.
y \u003d sin x функц.
Нэгж тойрог дээр x 0 нь цэгтэй тохирч байна ГЭХДЭЭ(Зураг 7), ба түүний тэнхлэг дээрх проекц OUцэг байх болно Н.Вфункцийн утга y 0 =нүгэл x0цэгийн ординатаар тодорхойлогддог ГЭХДЭЭ. Цэг AT(булан x 0 ,цагт 0) функцийн графикт хамаарна y= нүгэл x(Зураг 8). Функц нь тодорхой байна у=нүгэл xүе үе, түүний хугацаа нь 2 х:
нүгэл( x+ 2х) = нүгэл ( x).


Хоёр аргументийн утгын хувьд, Xба -, тэдгээрийн харгалзах цэгүүдийн төсөөлөл А хболон А-хтэнхлэг бүрт OUцэгийн ойролцоо тэгш хэмтэй байрлалтай О. Тийм ч учраас
нүгэл(- x) = -нүгэл ( x),
тэдгээр. синус нь сондгой функц, f(– x) = –f( x) (Зураг 9).

Хэрэв цэг бол Ацэгийн эргэн тойронд эргүүлнэ Обулангийн х/2 цагийн зүүний эсрэг (өөрөөр хэлбэл, хэрэв өнцөг X-ээр нэмэгдүүлнэ х/2), тэгвэл түүний шинэ байрлал дахь ординат нь хуучин байрлал дахь абсциссатай тэнцүү байна. Юу гэсэн үг вэ гэхээр
нүгэл( x+ х/2) = cos x.
Үгүй бол синус нь косинус, "хоцрогдсон" х/2, учир нь аргументын тоо нэмэгдэхэд аливаа косинусын утга синус дотор "давтагдах" болно х/2. Синусын график байгуулахын тулд косинусын графикийг өөр тийш шилжүүлэхэд хангалттай х/2 баруун тийш (Зураг 10). Синусын маш чухал шинж чанар нь тэгш байдалаар илэрхийлэгддэг

Тэгш байдлын геометрийн утгыг Зураг дээрээс харж болно. 11. Энд X -энэ бол нумын хагас юм AB, мөн нүгэл X -харгалзах хөвчний хагас. Мэдээжийн хэрэг, оноо ойртох тусам ГЭХДЭЭболон ATхөвчний урт нь нумын урттай ойртож байна. Ижил дүрсээс тэгш бус байдлыг гаргахад хялбар байдаг
|нүгэл x| x|, аль ч хүнд хүчинтэй X.

Томьёог (*) математикчид гайхамшигтай хязгаар гэж нэрлэдэг. Түүнээс, тухайлбал тэр гэм нүглийг дагадаг X» Xбагадаа X.
Функцүүд цагт=тг x, y=ctg X. Өөр хоёр тригонометрийн функцууд - тангенс ба котангенс нь бидний мэддэг синус ба косинусын харьцаагаар тодорхойлоход хялбар байдаг.
Синус ба косинусын нэгэн адил тангенс ба котангенс нь үечилсэн функц боловч тэдгээрийн үеүүд тэнцүү байна х, өөрөөр хэлбэл тэдгээр нь синус ба косинусын хоёр тал юм. Үүний шалтгаан нь тодорхой: хэрэв синус ба косинус хоёулаа тэмдгийг өөрчилвөл тэдгээрийн харьцаа өөрчлөгдөхгүй.
Шүргэгчийн хуваарьт косинус байдаг тул косинус 0 байх үед тангенс нь тодорхойлогдоогүй. X= х/2 +kp. Бусад бүх цэгүүдэд энэ нь монотоноор нэмэгддэг. Шууд X= х/2 + кпУчир нь шүргэгч нь босоо асимптотууд юм. Цэгүүд дээр кпшүргэгч ба налуу нь тус тус 0 ба 1 байна (Зураг 12).

Котангенс нь синус 0 байх үед тодорхойлогдоогүй (хэзээ x = kp). Бусад цэгүүдэд энэ нь monotonically буурч, шугамууд x = kp – түүний босоо асимптотууд. Цэгүүд дээр x = p/2 +kpкотангенс 0 болж хувирах ба эдгээр цэгүүдийн налуу нь -1 байна (Зураг 13).

Паритет ба үе үе.
Функцийг ч гэсэн дууддаг е(–x) = е(x). Косинус ба секантын функцууд тэгш, синус, тангенс, котангенс, косекант функцууд нь сондгой байна.
| sin(-α) = -sinα | tg (–α) = –tg α |
| cos(-α) = cosα | ctg(-α) = -ctgα |
| сек(-α) = секα | косек (–α) = – косек α |
Паритет шинж чанарууд нь цэгүүдийн тэгш хэмээс хамаарна Па ба Р-а (Зураг 14) тэнхлэгийн талаар X. Ийм тэгш хэмтэй бол цэгийн ординат тэмдэг өөрчлөгддөг (( X;цагт) руу явдаг ( X; -y)). Бүх функцууд - үе үе, синус, косинус, секант, косекант нь 2 үетэй байна х, ба тангенс ба котангенс - х:

| нүгэл (α + 2 кπ) = sinα | cos (α + 2 кπ) = cosα |
| бор (α + кπ) = tgα | ctg(α + кπ) = ctgα |
| сек (α + 2 кπ) = сек | косек (α + 2 кπ) = косека |
Синус ба косинусын үечилсэн байдал нь бүх цэгүүд байдаг П a + 2 кп, хаана к= 0, ±1, ±2,…, давхцах ба шүргэгч ба котангенсийн үечлэл нь цэгүүдтэй холбоотой. П a + кптойргийн диаметрийн эсрэг хоёр цэгт ээлжлэн унаж, шүргэгч тэнхлэгт ижил цэгийг өгнө.
Тригонометрийн функцүүдийн үндсэн шинж чанаруудыг хүснэгтэд нэгтгэн дүгнэж болно.
| Чиг үүрэг | Домэйн | Олон үнэт зүйл | Паритет | Нэг хэвийн байдлын бүсүүд ( к= 0, ± 1, ± 2,…) |
| нүгэл x | –Ґ x Ґ | [–1, +1] | хачин | -аар нэмэгддэг x O((4 к – 1) х /2, (4к + 1) х/2) гэж буурна x O((4 к + 1) х /2, (4к + 3) х/2) |
| cos x | –Ґ x Ґ | [–1, +1] | бүр | -аар нэмэгддэг xО((2 к – 1) х, 2кп), үед буурна xӨө (2 кп, (2к + 1) х) |
| тг x | x № х/2 + p k | (–Ґ , +Ґ ) | хачин | -аар нэмэгддэг xО((2 к – 1) х /2, (2к + 1) х /2) |
| ctg x | x № p k | (–Ґ , +Ґ ) | хачин | үед буурдаг xО ( кп, (к + 1) х) |
| сек x | x № х/2 + p k | (–Ґ , –1] БА [+1, +Ґ ) | бүр | -аар нэмэгддэг xӨө (2 кп, (2к + 1) х), үед буурна xО((2 к– 1) p , 2 кп) |
| шалтгаан x | x № p k | (–Ґ , –1] БА [+1, +Ґ ) | хачин | -аар нэмэгддэг x O((4 к + 1) х /2, (4к + 3) х/2) гэж буурна x O((4 к – 1) х /2, (4к + 1) х /2) |
Цутгах томъёо.
Эдгээр томьёоны дагуу a аргументийн тригонометрийн функцын утга, энд х/2 a p , аргументийн функцийн утга болгон бууруулж болно a , энд 0 a p /2, аль аль нь түүнтэй ижил ба нэмэлт.
| Аргумент b |  – а – а |
+ a | х– а | х+ a | + a | + a | 2х– а |
| нүгэл б | учир нь а | учир нь а | нүгэл а | – нүгэл а | -cos a | -cos a | – нүгэл а |
| cosb | нүгэл а | – нүгэл а | -cos a | -cos a | – нүгэл а | нүгэл а | учир нь а |
Тиймээс тригонометрийн функцүүдийн хүснэгтэд утгыг зөвхөн хурц өнцгийн хувьд өгдөг бөгөөд жишээлбэл, синус ба шүргэгчээр өөрсдийгөө хязгаарлахад хангалттай. Хүснэгтэнд зөвхөн синус болон косинусын хамгийн түгээмэл хэрэглэгддэг томъѐог агуулдаг. Тэдгээрээс шүргэгч ба котангенсийн томъёог олж авахад хялбар байдаг. Маягтын аргументаас функцийг дамжуулах үед кп/2 ± a , хаана к a аргументаас функц рүү бүхэл тоо:
1) хэрэв функцийн нэрийг хадгална ктэгш, хэрэв "нэмэлт" болж өөрчлөгдөнө ксондгой;
2) баруун талд байгаа тэмдэг нь цэг дээрх бууруулж болох функцын тэмдэгтэй давхцаж байна кп/2 ± a өнцөг нь хурц байвал.
Жишээлбэл, ctg (a -) дамжуулах үед х/2) эсэхийг шалгаарай a - х/2 at 0 a p /2 нь котангенс сөрөг байх дөрөв дэх квадратад байрладаг ба 1-р дүрмийн дагуу бид функцийн нэрийг өөрчилнө: ctg (a - х/2) = –tg a .
Нэмэлт томъёо.
Олон өнцгийн томъёо.
Эдгээр томъёог нэмэх томъёоноос шууд гаргаж авсан болно:
sin 2a \u003d 2 sin a cos a;
cos 2a \u003d cos 2 a - sin 2 a \u003d 2 cos 2 a - 1 \u003d 1 - 2 sin 2 a;
нүгэл 3а \u003d 3 нүгэл a - 4 гэм 3 а;
cos 3a \u003d 4 cos 3 a - 3 cos a;
Cos 3a-ийн томъёог Франсуа Вьет куб тэгшитгэлийг шийдвэрлэхдээ ашигласан. Тэрээр cos-ийн илэрхийлэлийг анх олсон хүн юм nа ба нүгэл n a , үүнийг хожим Де Мойврын томъёоноос илүү хялбар аргаар олж авсан.
Хэрэв та давхар аргументын томъёонд a-г /2-р сольсон бол тэдгээрийг хагас өнцгийн томьёо болгон хувиргаж болно:
Бүх нийтийн орлуулах томъёо.
Эдгээр томъёог ашиглан ижил аргументаас өөр өөр тригонометрийн функцуудыг агуулсан илэрхийллийг tg (a / 2) функцээс оновчтой илэрхийлэл болгон дахин бичиж болно, энэ нь зарим тэгшитгэлийг шийдвэрлэхэд хэрэг болно.
 |
|
 |
 |
Нийлбэрийг бүтээгдэхүүн, бүтээгдэхүүнийг нийлбэр болгон хөрвүүлэх томъёо.
Компьютер гарч ирэхээс өмнө эдгээр томъёог тооцооллыг хялбарчлахад ашигладаг байсан. Тооцооллыг логарифмын хүснэгт, дараа нь слайдын дүрэм ашиглан хийсэн, учир нь. логарифмууд нь тоог үржүүлэхэд хамгийн тохиромжтой байдаг тул бүх анхны илэрхийлэлүүдийг логарифмд тохиромжтой хэлбэр болгон бууруулсан. зэрэг ажилд зориулагдсан:
2 гэм анүгэл b = cos ( а-б) – учир нь ( a+b);
2 cos а cos б= учир ( а-б) + учир ( a+b);
2 гэм а cos б= нүгэл ( а-б) + нүгэл ( a+b).
Тангенс ба котангенсийн функцүүдийн томъёог дээрхээс авч болно.
Зэрэг бууруулах томъёо.
Олон аргументийн томъёоноос томъёог гаргаж авдаг:
| нүгэл 2 a \u003d (1 - cos 2a) / 2; | cos 2 a = (1 + cos 2a )/2; |
| нүгэл 3 а \u003d (3 нүгэл а - гэм 3а) / 4; | cos 3 a = (3 cos a + cos3 a )/4. |
Эдгээр томъёоны тусламжтайгаар тригонометрийн тэгшитгэлийг доод түвшний тэгшитгэл болгон бууруулж болно. Үүний нэгэн адил синус ба косинусын өндөр хүчийг бууруулах томъёог гаргаж болно.
| Тригонометрийн функцүүдийн дериватив ба интеграл | |
| (нүгэл x)` = cos x; | (cos x)` = -нүгэл x; |
| (тг x)` = ; | (ctg x)` = – ; |
| н нүгэл x dx= -cos x + C; | t cos x dx= нүгэл x + C; |
| t tg x dx= –ln |cos x| + C; | t ctg x dx = ln|sin x| + C; |
Тригонометрийн функц бүр өөрийн тодорхойлолтын талбарын цэг бүрт тасралтгүй бөгөөд хязгааргүй ялгаатай байдаг. Түүгээр ч зогсохгүй тригонометрийн функцүүдийн деривативууд нь тригонометрийн функцууд бөгөөд интегралдсан тохиолдолд тригонометрийн функцууд эсвэл тэдгээрийн логарифмуудыг олж авдаг. Тригонометрийн функцүүдийн оновчтой хослолын интеграл нь үргэлж энгийн функцууд байдаг.
Тригонометрийн функцуудыг чадлын цуваа ба хязгааргүй үржвэрийн хэлбэрээр илэрхийлэх.
Бүх тригонометрийн функцуудыг хүчирхэг цуваа болгон өргөжүүлж болно. Энэ тохиолдолд функцууд нь нүгэл үйлддэг x b cos xэгнээнд харагдана. бүх утгыг нэгтгэх x:
Эдгээр цувралууд нь нүглийн ойролцоо илэрхийлэлийг олж авахад ашиглагдаж болно xболон cos xжижиг утгуудын хувьд x:
дээр | x| p/2;
0x| дээр х
(Б n нь Бернуллигийн тоонууд).
нүгэл үйлдлүүд xболон cos xХязгааргүй бүтээгдэхүүнээр төлөөлж болно:
Тригонометрийн систем 1, cos x, нүгэл x, cos 2 x, гэм 2 x, ¼, cos nx, нүгэл nx, ¼, [– интервал дээр үүсдэг х, х] функцүүдийн ортогональ систем нь функцийг тригонометрийн цуваа хэлбэрээр дүрслэх боломжийг олгодог.
Бодит аргументийн харгалзах тригонометрийн функцүүдийн цогц хавтгайд аналитик үргэлжлэл гэж тодорхойлогддог. Тийм ээ, нүгэл zболон cos zнүгэлд зориулсан цувралыг ашиглан тодорхойлж болно xболон cos x, оронд нь бол xтавих z:
Эдгээр цувралууд бүхэл бүтэн хавтгайд нийлдэг тул нүгэл үйлддэг zболон cos zбүхэл бүтэн функцууд юм.
Тангенс ба котангенсыг дараах томъёогоор тодорхойлно.
tg функцууд zба ctg zнь мероморф функцууд юм. Польш тг zболон сек zэнгийн (1-р дараалал) бөгөөд цэгүүдэд байрладаг z=p/2 + pn, ctg шон zболон косек zнь бас энгийн бөгөөд цэгүүдэд байрладаг z = p n, n = 0, ±1, ±2,…
Бодит аргументын тригонометрийн функцүүдэд хүчинтэй бүх томъёо нь нарийн төвөгтэй аргументуудад бас хүчинтэй байна. Тухайлбал,
нүгэл(- z) = -нүгэл z,
учир нь(- z) = cos z,
тг(- z) = –тг z,
ctg (- z) = -ctg z,
тэдгээр. тэгш ба сондгой паритет хадгалагдана. Томьёог мөн хадгалсан
нүгэл( z + 2х) = нүгэл z, (z + 2х) = cos z, (z + х) = тг z, (z + х) = ctg z,
тэдгээр. үечлэл нь мөн хадгалагдаж, цэгүүд нь бодит аргументийн функцуудтай адил байна.
Тригонометрийн функцуудыг цэвэр төсөөллийн аргументийн экспоненциал функцээр илэрхийлж болно.
Буцах, e iz cos-ээр илэрхийлэгдэнэ zмөн нүгэл zтомъёоны дагуу:
e iz= cos z + бинүгэл z
Эдгээр томъёог Эйлерийн томъёо гэж нэрлэдэг. Леонхард Эйлер 1743 онд тэдгээрийг танилцуулсан.
Тригонометрийн функцийг мөн гипербол функцээр илэрхийлж болно.
z = –биШ из, cos z = ch iz, z = –i th iz.
Энд sh, ch ба th нь гиперболын синус, косинус ба тангенс юм.
Нарийн төвөгтэй аргументуудын тригонометрийн функцууд z = x + iy, хаана xболон y- бодит тоонуудыг бодит аргументуудын тригонометрийн болон гиперболын функцээр илэрхийлж болно, жишээлбэл:
нүгэл( x+iy) = нүгэл x ch y + би cos xШ y;
учир нь ( x+iy) = cos x ch y + бинүгэл xШ y.
Нарийн төвөгтэй аргументийн синус ба косинус нь үнэмлэхүй утгаараа 1-ээс их бодит утгыг авч болно. Жишээлбэл:
Хэрэв үл мэдэгдэх өнцөг нь тригонометрийн функцуудын аргумент болгон тэгшитгэлд орвол тэгшитгэлийг тригонометр гэж нэрлэдэг. Ийм тэгшитгэл нь маш түгээмэл тул тэдгээрийн аргууд шийдлүүд нь маш нарийн бөгөөд нарийн боловсруулсан. FROMянз бүрийн арга, томъёог ашиглан тригонометрийн тэгшитгэлийг хэлбэрийн тэгшитгэл болгон бууруулна е(x)= a, хаана е- хамгийн энгийн тригонометрийн функцүүдийн аль нэг нь: синус, косинус, тангенс эсвэл котангенс. Дараа нь аргументыг илэрхийл xэнэ функц нь мэдэгдэж буй утгаараа а.
Тригонометрийн функцууд нь үе үе байдаг тул адилхан аутгуудын хүрээнээс аргументийн хязгааргүй олон утгууд байдаг бөгөөд тэгшитгэлийн шийдлийг нэг функц болгон бичих боломжгүй. а. Тиймээс үндсэн тригонометрийн функц тус бүрийн тодорхойлолтын мужид өөрийн бүх утгыг зөвхөн нэг удаа авах хэсгийг сонгож, энэ хэсэгт урвуу функцийг олно. Ийм функцийг анхдагч функцийн нэрэнд нуман (нум) угтвар өгөх замаар тэмдэглэж, урвуу тригонометр гэж нэрлэдэг. функцууд эсвэл зүгээр л нуман функцууд.
Урвуу тригонометрийн функцууд.
Нүглийн төлөө X, cos X, тг Xба ctg Xурвуу функцийг тодорхойлж болно. Тэдгээрийг тус тус arcsin гэж нэрлэдэг X("арксин x"), аркос x, arctg xболон arcctg x. Тодорхойлолтоор, arcsin Xийм тоо байдаг у,юу
нүгэл цагт = X.
Бусад урвуу тригонометрийн функцүүдийн хувьд ч мөн адил. Гэхдээ энэ тодорхойлолт нь зарим нэг алдаатай байдаг.
Хэрэв бид гэм нүглийг тусгах юм бол X, cos X, тг Xба ctg XКоординатын хавтгайн эхний ба гурав дахь квадратуудын биссектрисатай харьцуулахад функцууд нь үечилсэн байдлаасаа болж хоёрдмол утгатай болдог: ижил синус (косинус, тангенс, котангенс) нь хязгааргүй тооны өнцөгтэй тохирч байна.
Тодорхой бус байдлаас салахын тулд өргөнтэй муруйн хэсэг х, харин аргумент болон функцын утгын хооронд нэг нэгээр нь харгалзах нь зайлшгүй шаардлагатай. Гарал үүслийн ойролцоох газруудыг сонгосон. Синусын хувьд "нэгээс нэгийн интервал" сегментийг авдаг тул [- х/2, х/2], үүн дээр синус монотоноор –1-ээс 1 хүртэл өсдөг, косинусын хувьд - сегмент , шүргэгч ба котангенсийн хувьд тус тус интервалууд (– х/2, х/2) ба (0, х). Интервал дахь муруй бүр нь биссектрисын талаар тусгагдсан бөгөөд одоо та урвуу тригонометрийн функцийг тодорхойлж болно. Жишээлбэл, аргументийн утгыг өгье x 0,Иймээс 0 Ж x 0 Ј 1. Дараа нь функцийн утга y 0 = арксин x 0 цорын ганц үнэ цэнэ байх болно цагт 0 , ийм - х/2 Ж цагт 0 Ј х/2 ба x 0 = нүгэл y 0 .
Тиймээс арксин нь арксинын функц юм а, [–1, 1] интервал дээр тодорхойлогдсон бөгөөд тус бүрдээ тэнцүү байна аийм утга a , – х/2 a p /2 that sin a = а.Үүнийг нэгж тойрог ашиглан дүрслэх нь маш тохиромжтой (Зураг 15). Хэзээ | a| 1 тойрог дээр ординат бүхий хоёр цэг байна а, тэнхлэгийн тэгш хэмтэй y.Тэдний нэг нь өнцөг юм а= арксин а, нөгөө нь өнцөг юм p - a. FROMсинусын үечлэлийг харгалзан син тэгшитгэлийн шийдэл x= адараах байдлаар бичигдсэн байна.
x =(–1)nнумын нүгэл а + 2p n,
хаана n= 0, ±1, ±2,...

Бусад энгийн тригонометрийн тэгшитгэлийг мөн шийддэг.
cos x = а, –1 =а= 1;
x=±аркос а + 2p n,
хаана П= 0, ±1, ±2,... (Зураг 16);

тг X = а;
x= arctg а + х n,
хаана n = 0, ±1, ±2,... (Зураг 17);

ctg X= а;
X= arcctg а + х n,
хаана n = 0, ±1, ±2,... (Зураг 18).

Урвуу тригонометрийн функцүүдийн үндсэн шинж чанарууд:
нумын нүгэл X(Зураг 19): тодорхойлолтын домэйн нь сегмент [–1, 1]; хүрээ - [- х/2, х/2], монотон нэмэгдэж буй функц;

arccos X(Зураг 20): тодорхойлолтын домэйн нь сегмент [–1, 1]; утгын хүрээ -; монотон буурах функц;

arctg X(Зураг 21): тодорхойлолтын домэйн - бүх бодит тоо; утгын хүрээ – интервал (– х/2, х/2); монотон нэмэгдэж буй функц; Чигээрээ цагт= –х/2 ба y \u003d p / 2 -хэвтээ асимптотууд;

arcctg X(Зураг 22): тодорхойлолтын домэйн - бүх бодит тоо; утгын хүрээ - интервал (0, х); монотон буурах функц; Чигээрээ y= 0 ба y = pхэвтээ асимптотууд юм.

Учир нь нийлмэл аргументын тригонометрийн функцууд нүгэл zболон cos z(бодит аргументийн функцээс ялгаатай нь) бүх нарийн төвөгтэй утгыг авч, тэгшитгэлүүд нь нүгэл болно. z = аболон cos z = ааливаа цогцолборын шийдэлтэй а хболон yбодит тоо, тэгш бус байдал байна
½| e\ey–э-y| ≤|нүгэл z|≤½( e y +e-y),
½| e y–э-y| ≤|cos z|≤½( e y +e -y),
нь y® Ґ асимптотик томьёо (хэрэгцээ жигд x)
|нүгэл z| » 1/2 д |у| ,
|cos z| » 1/2 д |у| .
Тригонометрийн функцүүд анх удаа одон орон, геометрийн судалгаатай холбоотойгоор үүссэн. Гурвалжин ба тойрог дахь сегментүүдийн харьцаа нь үндсэндээ тригонометрийн функцууд болох 3-р зуунд аль хэдийн олдсон. МЭӨ д. Эртний Грекийн математикчдын бүтээлүүдэд – Евклид, Архимед, Пергийн Аполлониус болон бусад боловч эдгээр харьцаа нь бие даасан судалгааны объект биш байсан тул тригонометрийн функцийг судлаагүй. Тэдгээрийг анх сегмент гэж үздэг байсан бөгөөд энэ хэлбэрээр Аристарх (МЭӨ 4-р зууны сүүл - 3-р зууны 2-р хагас), Гиппарх (МЭӨ 2-р зуун), Менелаус (МЭ 1-р зуун) ба Птолемей (МЭ 2-р зуун) ашиглаж байжээ. бөмбөрцөг гурвалжныг шийдвэрлэх. Птолемей 10 -6 нарийвчлалтайгаар 30 хүртэлх хурц өнцгийн хөвчүүдийн эхний хүснэгтийг эмхэтгэсэн. Энэ бол синусын анхны хүснэгт байсан. Харьцааны хувьд sin a функц нь Ариабхатад (5-р зууны төгсгөл) аль хэдийн олддог. tg a болон ctg a функцууд нь аль-Баттани (9-р зууны 2-р хагас - 10-р зууны эхэн) ба Абул-Вефа (10-р зууны) -д байдаг бөгөөд тэд бас sec a, cosec a ашигладаг... Арьябхата томъёог аль хэдийн мэддэг байсан ( sin 2 a + cos 2 a) \u003d 1, түүнчлэн хагас өнцгийн син ба кос томьёо, тэдгээрийн тусламжтайгаар тэрээр 3 ° 45-аас дээш өнцгүүдийн синусын хүснэгтүүдийг барьсан; хамгийн энгийн аргументуудын хувьд тригонометрийн функцүүдийн мэдэгдэж буй утгууд дээр үндэслэсэн. Бхаскара (12-р зуун) нэмэх томъёог ашиглан 1-ээр дамжуулан хүснэгт байгуулах аргыг өгсөн. Төрөл бүрийн аргументуудын тригонометрийн функцүүдийн нийлбэр ба зөрүүг үржвэрт хувиргах томьёог Региомонтанус (15-р зуун), Ж.Напиер нар логарифмийг (1614) зохион бүтээсэнтэй холбогдуулан гаргаж авсан. Regiomontanus 1 "-ээр дамжуулан синусын утгуудын хүснэгтийг өгсөн. Тригонометрийн функцийг зэрэглэлийн цуваа болгон өргөтгөхийг I. Newton (1669) олж авсан. L. Euler (18-р зуун) тригонометрийн функцүүдийн онолыг орчин үеийн хэлбэрт оруулсан. Тэрээр синус ба косинусын системийн экспоненциал функц, ортогональ байдалтай холбоо тогтоож, одоо бэлгэдлээр хүлээн зөвшөөрөгдсөн бодит ба төвөгтэй аргументуудын тодорхойлолтыг эзэмшдэг.
|BD| - А цэг дээр төвлөрсөн тойргийн нумын урт.
α нь радианаар илэрхийлэгдсэн өнцөг юм.
шүргэгч ( tgα) нь тэгш өнцөгт гурвалжны гипотенуз ба хөлийн хоорондох α өнцөгөөс хамаарах тригонометрийн функц бөгөөд эсрэг талын хөлийн уртын харьцаатай тэнцүү |BC| зэргэлдээх хөлний урт хүртэл |AB| .
Котангенс ( ctgα) нь тэгш өнцөгт гурвалжны гипотенуз ба хөлийн хоорондох α өнцөгөөс хамаарах тригонометрийн функц бөгөөд зэргэлдээх хөлийн уртын харьцаатай тэнцүү |AB| эсрэг талын хөлний урт хүртэл |BC| .
Тангенс
Хаана n- бүхэлд нь.
Барууны уран зохиолд шүргэгчийг дараах байдлаар тэмдэглэсэн байдаг.
.
;
;
.
Шүргэх функцийн график, y = tg x

Котангенс
Хаана n- бүхэлд нь.
Барууны уран зохиолд котангенсыг дараах байдлаар тэмдэглэсэн байдаг.
.
Дараах тэмдэглэгээг мөн баталсан.
;
;
.
Котангенсийн функцийн график, y = ctg x

Тангенс ба котангенсын шинж чанарууд
Үе үе
y= функцууд tg xба y = ctg xπ үетэй үечилсэн байна.
Паритет
Тангенс ба котангенс функцууд нь сондгой.
Тодорхойлолт ба утгын хүрээ, өсөх, буурах
Тангенс ба котангенс функцууд нь тодорхойлолтын талбартаа тасралтгүй байдаг (тасралтгүй байдлын баталгааг үзнэ үү). Тангенс ба котангентын үндсэн шинж чанарыг хүснэгтэд үзүүлэв ( n- бүхэл тоо).
| у= tg x | у= ctg x | |
| Хамрах хүрээ ба тасралтгүй байдал | ||
| Утгын хүрээ | -∞ < y < +∞ | -∞ < y < +∞ |
| Өгсөж байна | - | |
| Бууж байна | - | |
| Хэт их | - | - |
| Тэг, у= 0 | ||
| У тэнхлэгтэй огтлолцох цэгүүд, x = 0 | у= 0 | - |
Томъёо
Синус ба косинусын илэрхийлэл
;
;
;
;
;
Нийлбэр ба ялгаварын тангенс ба котангенсийн томъёо
Жишээлбэл, бусад томъёог олж авахад хялбар байдаг
Шүргэгчийн бүтээгдэхүүн
Шүргэгчийн нийлбэр ба зөрүүний томъёо
Энэ хүснэгтэд аргументийн зарим утгуудын шүргэгч ба котангентын утгыг харуулав. 
Комплекс тоонуудын илэрхийлэл
Гиперболын функцүүдийн илэрхийлэл
;
;
Дериватив
; .
.
Функцийн х хувьсагчийн хувьд n-р эрэмбийн дериватив:
.
Шүргэгчийн томьёо гарган авах > > > ; котангенсийн хувьд > > >
Интеграл
Цуврал болгон өргөтгөх
X-ийн зэрэглэлийн тангенсийн тэлэлтийг авахын тулд функцүүдийн хүчирхэг цувралын өргөтгөлийн хэд хэдэн нөхцөлийг авах шаардлагатай. гэм хболон cos xмөн эдгээр олон гишүүнтүүдийг хооронд нь хувааж, . Үүний үр дүнд дараах томъёо гарч ирнэ.
-д.
цагт.
хаана Б н- Бернуллигийн тоо. Тэдгээрийг дахилтын хамаарлаас аль нэгээр нь тодорхойлно.
;
;
хаана.
Эсвэл Лапласын томъёоны дагуу: 
Урвуу функцууд
Тангенс ба котангенсийн урвуу функцууд нь арктангенс ба арккотангенс байна.
Арктангенс, арктг
, хаана n- бүхэлд нь.
Нуман тангенс, arcctg
, хаана n- бүхэлд нь.
Лавлагаа:
И.Н. Бронштейн, К.А. Семендяев, Дээд боловсролын байгууллагын инженер, оюутнуудад зориулсан математикийн гарын авлага, Лан, 2009 он.
Г.Корн, Судлаач, инженерүүдэд зориулсан математикийн гарын авлага, 2012 он.
Үндсэн ойлголтууд
Тодорхойлолтуудаас эхэлье тэгш, сондгой, үечилсэн функцууд.
Тодорхойлолт 2
Бие даасан хувьсагчийн тэмдэг өөрчлөгдөхөд утга нь өөрчлөгддөггүй функцийг тэгш функц гэнэ.
Тодорхойлолт 3
Тодорхой хугацааны интервалаар утгуудаа давтдаг функц:
T нь функцийн үе юм.
Тэгш ба сондгой тригонометрийн функцууд
Дараах зургийг авч үзье (Зураг 1).
Зураг 1.
Энд $\overrightarrow(OA_1)=(x_1,y_1)$ ба $\overrightarrow(OA_2)=(x_2,y_2)$ нь $Ox$ тэнхлэгтэй харьцуулахад тэгш хэмтэй байна. векторууд ганц биеурт.
Мэдээжийн хэрэг, эдгээр векторуудын координатууд нь дараах харилцаатай холбоотой байдаг.
Синус ба косинусын тригонометрийн функцийг нэгж тригонометрийн тойрог ашиглан тодорхойлж болох тул синус функц нь сондгой, косинусын функц нь тэгш функц байх болно, өөрөөр хэлбэл:
Тригонометрийн функцүүдийн үечлэл
Дараах зургийг авч үзье (Зураг 2).

Зураг 2.
Энд $\overrightarrow(OA)=(x,y)$ нь нэгж урттай вектор байна.
$\overrightarrow(OA)$ вектороор бүтэн эргэлт хийцгээе. Өөрөөр хэлбэл, өгөгдсөн векторыг $2\pi $ радианаар эргүүлье. Үүний дараа вектор анхны байрлалдаа бүрэн буцаж ирнэ.
Синус ба косинусын тригонометрийн функцийг нэгж тригонометрийн тойрог ашиглан тодорхойлж болох тул бид үүнийг олж авна.
Өөрөөр хэлбэл, синус болон косинусын функцууд нь $T=2\pi $ хамгийн бага үетэй үечилсэн функцууд юм.
Одоо тангенс ба котангенсийн функцуудыг авч үзье. $tgx=\frac(sinx)(cosx)$ тул
$сtgx=\frac(cosx)(sinx)$ тул
Тригонометрийн функцүүдийн тэгш, сондгой, үечилсэн байдлыг ашиглах асуудлын жишээ
Жишээ 1
Дараах мэдэгдлийг нотлох:
a) $tg(385)^0=тг(25)^0$
в) $sin((-721)^0)=-sin1^0$
a) $tg(385)^0=тг(25)^0$
Шүргэгч нь $(360)^0$ хамгийн бага хугацаатай үечилсэн функц тул бид олж авна
б) $(cos \left(-13\pi \right)\ )=-1$
Косинус нь хамгийн бага хугацаа $2\pi $ байх тэгш ба үечилсэн функц тул бид олж авна
\[(cos \left(-13\pi \баруун)\ )=(cos 13\pi \ )=(cos \left(\pi +6\cdot 2\pi \баруун)=cos\pi \ )=- нэг\]
в) $sin((-721)^0)=-sin1^0$
Синус нь хамгийн бага хугацаа $(360)^0$ байх сондгой, үечилсэн функц тул бид олж авна.